机器之心报道

所有学LLM的人都要知道的内容。

这可能是对于大语言模型（LLM）原理最清晰、易懂的解读。

前段时间，GoogleDeepMind的首席科学家兼研究总监DennyZhou在斯坦福大学的CS25课程中，分享了大语言模型推理的深刻洞见。

作为人工智能领域的领军人物，DennyZhou通过这场讲座对LLM推理机制及其优化方法进行了系统阐述，揭示了大模型推理的核心原理和最新进展。

DennyZhou总结了四个关键点：

LLM中的推理仅仅意味着在得出最终答案之前生成一系列中间token，这是否与人类推理相似并不重要，关键在于，Transformer模型通过生成许多中间token，可以变得极其强大，而无需扩展模型的大小。

预训练模型即使未经任何微调，也具备推理能力。挑战在于，基于推理的输出往往不会出现在输出分布的顶部，因此标准贪婪解码无法将它们呈现出来。

提示技巧（例如思维链提示或「让我们一步一步思考」）和监督式微调曾是引发推理的常用方法，现在强化学习微调已成为最强大的方法，这一技巧被多个实验室独立发现。在谷歌，这要归功于团队成员JonathanLai，基于理论，扩展强化学习应该专注于生成长响应，而不是其他目标。

通过生成多个响应然后将它们聚合起来，而不是依赖于单个响应，可以极大地提高LLM推理能力。

DennyZhou不仅是GoogleDeepMind的顶尖科学家，还曾在GoogleBrain创立并领导了推理团队（ReasoningTeam），现在该团队是DeepMind的一部分，专注于开发具备推理能力的大语言模型，以推动人工智能通用智能的发展。

他的研究聚焦于链式思考提示（chain-of-thoughtprompting）、自一致性（self-consistency）和LLM优化等领域，在GoogleScholar上累计获得超过83,000次引用，对机器学习和AI领域贡献显著。

此外，他还共同创办了语言建模大会（CoLM），并担任2024年大会的总主席，曾荣获2022年GoogleResearchTechImpactAward和WSDMTestofTimeAward，并在KDD2023等活动中发表主题演讲。他常在斯坦福、哈佛等大学进行邀请讲座，分享关于LLM的观点。

他参与教学的CS25《TransformersUnitedV5》课程，目前已是斯坦福大学最热门、最具研讨性的课程之一，汇聚了GeoffreyHinton、AshishVaswani和AndrejKarpathy等我们耳熟能详的AI顶尖研究人员。该课程在斯坦福大学内外都广受欢迎，YouTube上的观看次数更是高达数百万。每个星期，人们在课上都会深入探讨人工智能领域的最新突破，从GPT等大型语言模型到艺术、生物和机器人领域的应用。

课程页面：https://web.stanford.edu/class/cs25/

接下来，让我们看看AI领域的顶级学者是如何解读大模型「推理」这一至关重要的能力的。

如今，很多人都已经相信大语言模型（LLM）是可以推理的了。实际上，我们还不知道这是否成立，这可能取决于对推理的定义。在这里，我们认为推理是输入问题-输出答案之间的中间步骤（生成的token）。

LLM中的推理仅仅意味着在得出最终答案之前生成一系列中间token，这是否类似于人类的推理并不重要，关键在于，Transformer模型可以通过生成大量中间token而变得几乎任意强大，而无需扩展模型大小。

为什么中间token在推理中至关重要？

Denny认为，在推理中中间token的作用至关重要。他与斯坦福大学的Tayma教授及其学生合作，提出了一个理论：任何可以通过布尔电路解决的问题，都可以通过生成中间token来用恒定大小的transformer模型解决。

这个理论表明，逻辑电路的大小（即电路中逻辑门的数量）决定了解决问题的能力。比如，使用GPU集群时，逻辑门的数量可能达到数千万、数十亿甚至数万亿。如果直接生成最终答案，可能需要极深的模型结构，甚至无法解决问题。而通过生成中间token，模型就能以恒定大小的transformer架构有效地解决问题。这种思路提供了一种从理论角度理解推理的方式。

推理过程的技术细节

关于推理的一个常见看法是，语言模型不能推理，除非进行进一步的提示工程，比如安全提示或候选答案的微调，我同意这个观点。我们可以简单地认为，语言模型已经具备了推理能力，关键在于解码过程。

举个例子。这道简单的数学问题：「我有3个苹果，我爸爸比我多2个苹果。我们一共有多少个苹果？」如果你使用任何预训练模型，比如Llama、DeepSeek或Qwen，直接输入这个问题，模型可能会输出「5个苹果」，这是错误的。

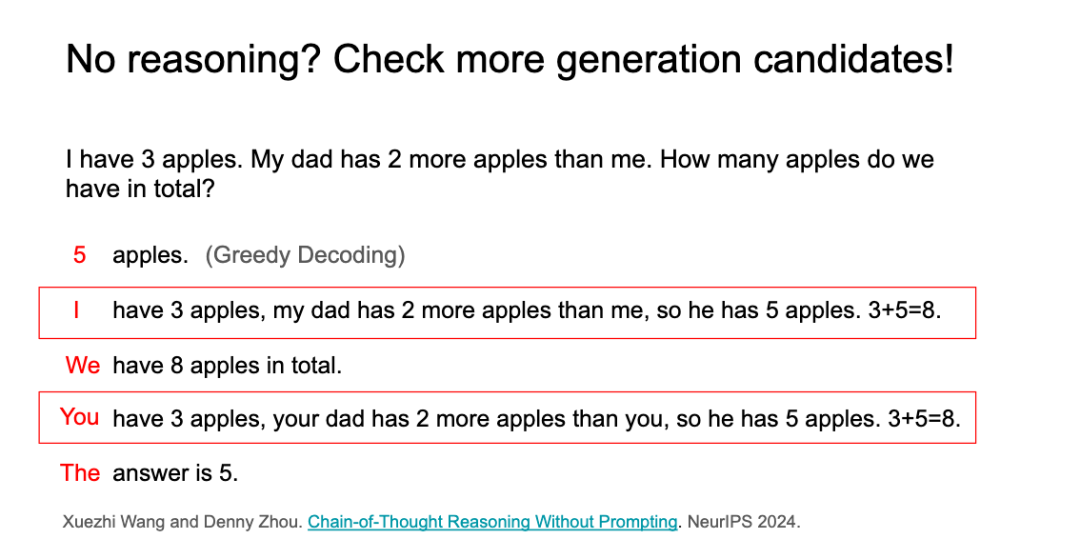
这是因为使用了「贪婪解码」方法，模型直接输出最可能的答案。但是，如果我们多考虑一些候选答案，而不是只选择一个最可能的候选答案，模型就能产生一个更正确的答案，这就是「链式推理解码」的概念。

它包含两个步骤：第一步，超越贪婪解码，检查更多的生成候选；第二步，选择那些最终答案置信度更高的候选。

链式推理解码是一个非常简单的方法，但它需要一些程序设计工作。我们还可以尝试其他方法，如通过简单的自然语言提示，直接指导模型进行链式推理，这就是「链式思维提示」奏效的原因。通过这种方法，我们可以使推理过程自然地出现在输出空间中，而不需要复杂的计算步骤。

这些提示方法确实非常简单，而且效果也非常好，但我们也能看到一些问题，例如安全提示方法就需要任务特定的示例。而另一个方法叫做「逐步思考」，它是一个通用的方法。你不需要找到类似的示例，只需说「让我们一步步思考」，然后奇迹般的结果就会出现。不过，它的表现比少量示例的提示差得多。

虽然这两种方法看起来都不错，但「逐步思考」方法有些怪。如果我问某人一个问题，然后要求他们跟我一步步思考，否则他们就无法继续思考，这显然不符合我们的期望。

现在有一种流行的方法：监督微调（SFT）。

实际上思路非常简单，我们可以从人工标注者那里收集一系列问题及其逐步解决的方案，然后我们最大化人类解决方案的可能性，标记一些实际上用于LLM训练的网络代码。在那之后，我们就可以在任何地方应用这个模型。DennyZhou等人在2017年的一系列研究中展示了这种能力，他们收集了大量文字问题及人工标注的解决方法。在2021年，这一方法被用来解决大规模问题，随后OpenAI扩展了这一方法。

这是简单的工作原理示意：用一系列例子、问题和答案微调你的模型，然后就可以在新的问题上进行测试了。比如这里就是众多大模型难以回答的strawberry单词里有多少个r的问题。很多人一度认为这个问题是用于测试AGI是否出现的「重大问题」。

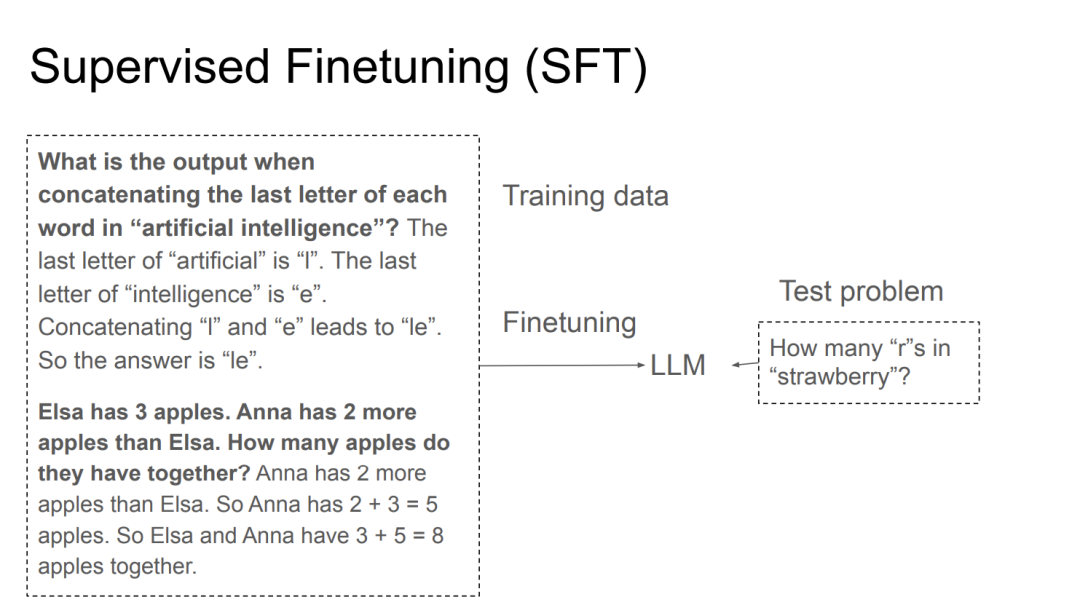
SFT实际上是一个通用的方法，如果这就能解决AI的推理问题，那事情就太简单了，然而它的泛化能力是有限的。DeepMind在2021年夏天意识到了这个问题，怎么办？只有Scaling,Scaling,Scaling，找到更多数据来进行训练，看看效果如何。

但这里有个教训，不要盲目扩展规模，方向错了就什么也得不到。

如何解决SFT泛化失败的问题？有两个重要方面，首先是解决人类标注错误的问题。实际上谷歌一个发明finetuning研究的成员曾表示，他们发现机器生成的数据可能还要优于人类构建的数据。这是个有点反直觉的经验。

让AI实现自我提升

所以第一波尝试被称作自我提升，与其从人类那里生成、收集数据，我们可以直接让模型生成数据。所以收集问题的数据集，你的模型要逐步生成解决方案，然后再次最大化正确答案的可能性。

比如一个数学问题，你有问题和答案，让大模型生成解决问题的步骤，依据是否获得正确答案来选择正确的步骤。这就是RejectSampling，这里唯一的区别在于数据来自于你的模型，而非人类。

该研究的论文即《STaR:BootstrappingReasoningWithReasoning》，其本意是减少昂贵的人工标注成本。但从另一个角度来理解，一旦更好的模型生成了响应或训练数据，模型就可以自我改进。

模型获得了改进之后，又该从哪里收集数据呢？我们可以重复这个过程。

我们注意到字节跳动研究人员在2024年1月发在arXiv上的《ReFT:ReasoningwithReinforcedFine-Tuning》，这可能是RLfinetuning的最早的学术出版物。甚至论文标题都叫做《基于强化调优的推理》。随后，在OpenAI的o1公开之后，每个人都开始意识到要使用强化学习微调了。

可能有很多研究团队独立意识到了这个方向。

强化学习先驱RichSutton在《Verification,thekeytoAI》中曾提到，在RL微调中，可靠的验证器是最关键的，而非RL算法。

那么问题来了，除了效率问题以外，为什么机器生成的训练数据反而比人类的更好？

这与机器学习中的第一性原理相关，即直接优化我们想要的东西。如果我们想构建一个用于推理的模型，或者只是一般地用于生成有趣的内容，我们就需要优化衡量生成质量的指标。一旦你有了一个度量标准，我们所需要做的就是计算该度量标准的梯度并进行反向传播。

因此，假设模型是一个先验的模型，我们需要最大化该指标的期望值。那么该怎么做呢？我们需要进行采样来计算期望值，这就是你得到策略梯度的原因。

这里没有魔法（比如如何激励你的模型进行同步，激活多个位置），不需要那些词汇，这里只使用标准的机器学习术语，定义你的指标，计算梯度并进行反向传播。

现在，这个方法运行良好，那么就该Scaling了。朝哪个方向扩展呢？粗略地考虑，似乎随着COT的增长，一个模型可以解决所有的问题，这都不需要模型尺寸的增长，只需要最小的固定大小的迁移模型，这样也没关系。

所以你如果查阅早期文献会发现，人们认为RLfinetuning效果好于SFT。

这里不得不说到LLM推理的美妙之处了。这个类似于人类的推理过程源自逐个token的预测，而非像传统AI那样依赖搜索排序。

举个例子，2024年12月，谷歌发布了Gemini2.0思考模式，这里尝试了一个训练集里没有的问题。使用1到10的数字来组成2025，并且明智地使用每个数字以及加法和乘法这两种基本运算。

右边可以看到Gemini2.0的思考过程，让我们看看模型是如何进行思考的。这不是通过搜索。你可以看到，在一开始，模型就表示这是一个相对较大的数字，这表明乘法运算将大量涉及。这就像人类思考一样。值得注意的是，2025是45的平方，即45乘以45。接着模型开始思考如何得到中间产物，使用乘法……

这就是模型训练如此强大的原因。

再次引用RichSutton在《苦涩的教训》中的话：Scaling的发现只会让我们更难看清发现过程是如何完成的。

看起来，Sutton在看到DeepMind的AlphaGo和AlphaZero的成功之后，写出了《苦涩的教训》。真正可扩展的只有两个过程，一个是学习，另一个是搜索。在这里我只想强调一件事。学习是可扩展的，我们只需要学习。

RLfinetuning的优势在于它的泛化很好，但并不是所有任务都是可以由机器自己进行验证的，比如写作，甚至代码编程。

我们必须牢记，LLM是进行预测的模型，他们不是人类。

从数学角度来看，这意味着什么？我们来思考一下LLM的解码过程。给定问题和生成器推理，然后输出最终答案，接着是通过网格解码关键找到的响应，那么关键点就是匹配概率。

对我们来说，需要选择概率最大的答案。所以它们没有对齐，我们只需要再进一步。如果我们生成推理过程，我们应该有一些整体推理过程来找出最终答案在机器学习方面的概率，这被称为边缘化。所有这些原因实际上本质上都只是潜在变量。如果我们刚开始接触机器学习，实际上就会知道这个和可以通过采样来计算。

因此，通过随机抽样生成多个响应，然后选择出现频率最高的答案。我们不看推理通过率，它只选择最常见的答案，而不是最常见的任务通过率。这就是诀窍。这在实证中被称为边缘化。如果你采用这种方法，就会看到巨大的改进。

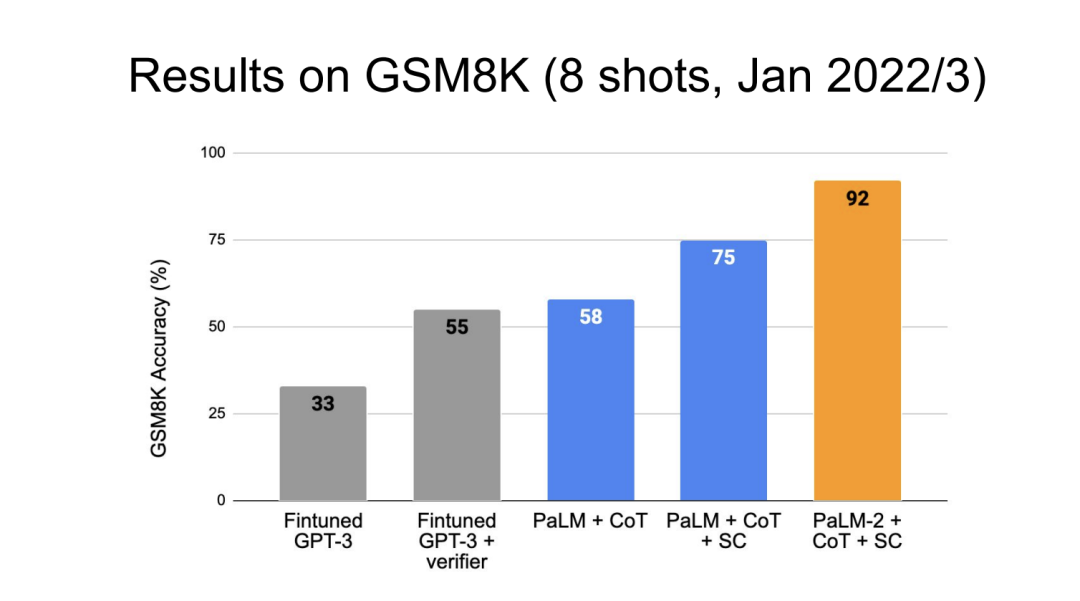
另一种方法是检索。我知道关于检索推理有很多辩论，很多人说语言模型可能只是做检索而不是推理，对我来说，实际上总是很难区分检索和推理。

我每年都会参加几乎每一场会议，每次我们都会讨论每篇论文的新颖性。其实，检索和推理的辩论就像是类似的争论。我看到过一个实验，尝试不同的模型并行运行，这样做可能会让结果更混乱。比如，使用4个不同的模型回答同一个问题，最后再对比答案，挑选出最一致的结果。

如果从不同模型中生成回答，这更像是一种「模型组合」（modelassembly）方法，通过多个模型的输出进行对比，选择一个最佳答案，类似于随机选择。虽然数学原理不完全相同，但它们的实现方式是类似的。

关于检索和推理的争论，我个人并不太关注。我在工业界工作，更关注的是实际性能。对我来说，如果检索能够获得A+级的答案，那为什么还要争论是否属于推理呢？所以，2024年我们发布了一篇关于类比推理的论文。我可以用一个小例子来展示检索在推理中的重要性。

考虑这样一个问题：一个正方形的四个顶点的坐标是……那么它的面积是多少？这个红色高亮部分是我添加的提示：「回忆一个相关的问题，然后解决这个问题。」

当时，我尝试了GPT3.5和我们自己的模型，但它们在没有提示的情况下无法解答这个问题。然而，添加了相关问题的提示后，模型就能解决这个问题了。

发生了什么呢？当我告诉模型回忆相关问题时，模型找到了一个相关但不同的问题。其实，这是一个与当前问题相关的问题，涉及计算坐标平面上两点之间的距离，并给出了公式。然后，模型说：「哦，我现在知道如何计算距离了，接着我就可以计算面积。」这个例子展示了检索在推理中的重要性。

另一个例子是「后退一步」的方法。在解决问题之前，我们给模型提供了一些简短的例子，让它理解如何抽象化思考。例如，在解决实际问题之前，我们可以让模型「后退一步」，思考更抽象的原则，然后再应用到实际问题中。这就是检索在推理中的作用。

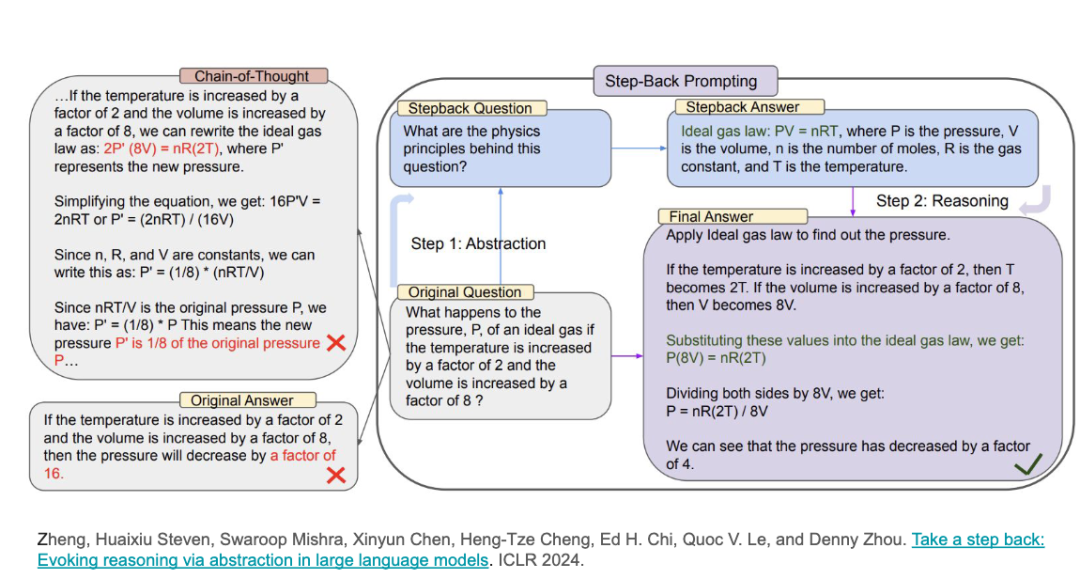
我想现在大家都明白，深度学习研究（DeepResearch）团队的理念也与此类似。我们有一个叫做「深度研究」的团队，其中一位负责人曾是我的实习生。后来，他加入了OPI并发明了「深度研究」方法。你们看到的区别就在于，他们通过检索相关问题或知识，帮助解决实际问题，基本思路其实非常简单。

最后，DennyZhou进行了总结：其实大家不必再纠结AMS是否能够推理，至少在语言模型中，推理总是比没有推理更好，Alpha微调比SFT（监督微调）更好，聚合多个答案比只选一个答案更好，当然，这会更昂贵。而检索和推理的结合比单纯的推理要好得多。

对于未来的突破，DennyZhou表示，他非常期待看到如何解决那些超出唯一、可验证答案的任务。他认为，基准测试很快会趋于饱和，更多的研究应该集中在构建真正的应用程序上，而不仅仅是解决学术性基准测试问题。

DennyZhou引用了RichardFeynman的名言：「真理总是比你想象的更简单。」他强调，这句话对于机器学习研究尤其适用。很多学术论文过于复杂，但实际上，我们的研究可以保持简洁明了。

参考链接：