在7月底结束的2024年东南地区数学奥林匹克中，高二年级组的最后一题是一道和二进制有关的题目：

这道题目第一问的解答需要先证明一个引理，然后利用该引理来解答：

其实这个引理的证明过程多少有些类似计算机编程中的位运算，笔者盲猜这道题目或许也是根据信息技术中的某个内容编制的。

看到这个题目，笔者想起了十年前的2014年西部数学邀请赛的最后一题，题目如下：

解答过程需要用到分类讨论：

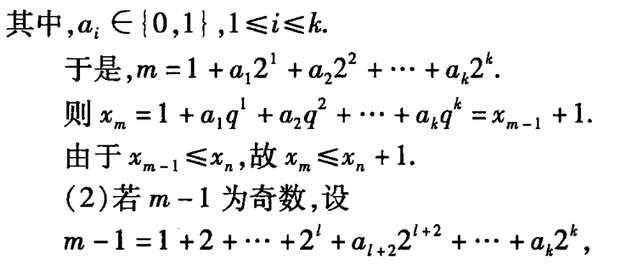
这道题目多少类似2014年天津高考数学数列题目(理科第19题，文科第20题)

这道题目给出的答案如下：

其实这道题目第一问就是利用二进制，x1，x2，x3的值从(0,0,0)到(1,1,1)就得到A的取值范围，而第二问则在进制基础上使用了一点所谓极端原理(ai都取0，bi都取q-1)。

这里补充一点，2014年西部数学邀请赛是在2014年八月份进行的，比2014年高考差不多晚了2个月。不知道这道题目的命题人是不是参考了天津这道高考题还只是说是碰巧类似，这个只能有机会去请教一下命题人了。

其实二进制在高考题目中已经出现很多次了。早的不说，从2010年开始，除了2014年天津这次，2010年湖北省文科高考数学试卷，2011年湖南理科数学试卷的填空压轴题以及2021年新高考二卷(海南、辽宁、重庆三省市)的多选压轴题目都出现过，而在2024届东北三校一模压轴题中则把前面几个题的内容“合成”了一下作为新题型出现，具体解法参见笔者之前文章《从24届东北三校一模压轴题聊聊新定义题目的一种复习思路》。

不知道今年这道东南奥林匹克这道题会不会在随后的高考模拟题中改编一下再次出现，咱们拭目以待！