行测题库｜数量关系｜每日一练：数学运算47

例题1

生产一件甲产品消耗4份原料A、2份原料B、3份原料C，可获得1.1万元利润；生产一件乙产品3份原料A、5份原料B，可获得1.3万元利润。现有40份原料A、38份原料B、15份原料C用于生产，问最多可获得多少万元利润？

A.10.2

B.12.0

C.12.2

D.12.8

解析：

根据题意，可知只有甲产品使用C原料。

当生产15÷3=5件甲产品时C正好用完。

A原料还剩40-3×5=25（份），B原料还剩38-2×5=28（份）。此时还可生产28÷5≈5件乙产品。

总利润为(1.1+1.3)×5=12万元。

由于每件乙产品的利润更高，应考虑少生产一件甲产品的情况。

若生产4件甲产品，则可生产6件乙产品。总利润为1.1×4+1.3×6=12.2万元，为最大利润。

因此，选择C选项。

例题2

某中学在高考前夕进行了四次语文模拟考试，第一次得90分以上的学生为70%，第二次是75%，第三次是85%，第四次是90%，请问在四次考试中都是90分以上的学生至少是多少？

A.40%

B.30%

C.20%

D.10%

解析：

（1）反向：第一次考试未过90分的学生为1－70%＝30%；第二次为25%、第三次为15%、第四次为10%；

（2）加和：未过90分的学生最多为30%＋25%＋15%＋10%＝80%；

（3）作差：四次考试中都是90分以上的学生至少是100%－80%＝20%。

因此，选择C选项。

知识点：

反向思路：反向——加和——做差。

例题3

某县政府组织干部职工开展党建知识竞赛，其中甲、乙两镇参赛人数之比为4∶3，甲镇有8人、乙镇有24人没有参加竞赛。已知甲、乙两镇干部职工人数之比为5∶6，则乙镇的干部职工比甲镇多（）人。

A.8

B.7

C.6

D.5

解析：

根据“甲、乙两镇参赛人数之比为4∶3”，可设甲镇参赛人数为4x，乙镇参赛人数为3x。

根据题意可列方程：（4x＋8）∶（3x＋24）＝5∶6，解得x＝8。

故甲镇干部职工共有4×8＋8＝40（人），乙镇干部职工共有3×8＋24＝48（人），乙比甲多48－40=8（人）。

因此，选择A选项。

例题4

某网店的甲商品定价为300元，乙商品定价为500元。小张以七折购买了甲商品，购买乙商品时参加了每满199元减50元的活动。小赵购买甲商品时在9折基础上又参加了每满100元减10元活动，则小赵通过以下哪种促销活动购买乙商品，其购买甲、乙两件商品总花销与小张一样？

A.减50元后打八折

B.直接打七折

C.打九折后减120元

D.直接减120元

解析：

根据“小张以七折购买了甲商品”，可知：小张买甲商品花了300×0.7＝210（元）；

根据“购买乙商品时参加了每满199元减50元的活动”，可知：小张买乙商品花了500－100＝400（元）；

小张一共花了210＋400＝610（元）。

根据“小赵购买甲商品时在9折基础上又参加了每满100元减10元活动”，可知：小赵买甲商品花了300×0.9－20＝250（元）。

要想小赵与小张花费相同，小赵购买乙商品需花费610－250＝360（元）。

代入选项验证：

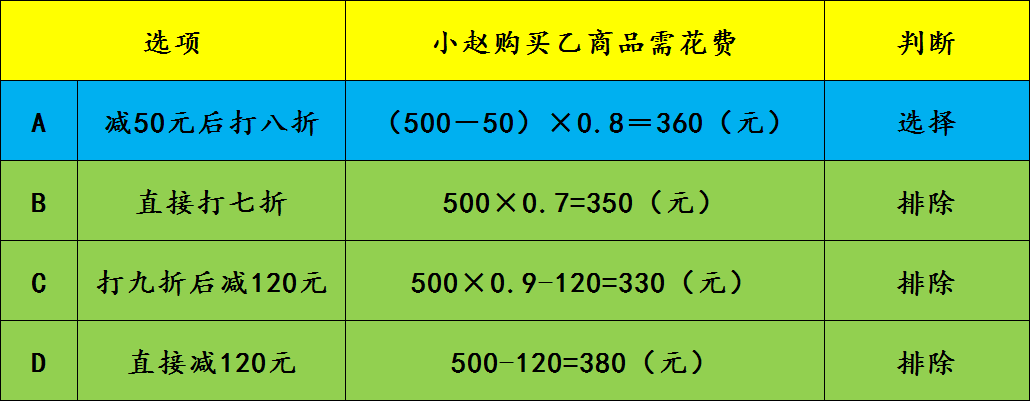
代入A选项，小赵购买乙商品需花费（500－50）×0.8＝360（元），满足题意，故A选项正确。

因此，选择A选项。

例题5

2020年时，李某的年龄是自己工龄的4倍，且正好是张某年龄的2/3。到2024年时，张某的年龄正好是自己工龄的2倍。已知张某参加工作时李某10岁，那么李某参加工作时的年龄是：

A.18岁

B.21岁

C.24岁

D.27岁

解析：

根据“2020年时，李某的年龄是自己工龄的4倍”，可设2020年李某的工龄为x岁，则李某当年4x岁。

根据“2020年时，李某的年龄是张某年龄的2/3”，可知张某的年龄为（4x÷2/3）岁，化简得6x岁。

到2024年时，即四年后，李某年龄为（4x+4）岁，张某的年龄为（6x+4）岁。

根据“到2024年时，张某的年龄正好是自己工龄的2倍”，可知：张某2024年的工龄为[（6x+4）÷2]岁，化简得（3x+2）岁，则2020年工龄为（3x+2-4）岁，化简得（3x-2）岁。

根据“张某参加工作时李某10岁”，可知：李某年龄-张某工龄=10。

可列方程：4x-（3x-2）=10，解得x=8岁。

所以李某参加工作的年龄为4x-x=24岁。

因此，选择C选项。

知识点：

年龄-工龄=参加工作时间。