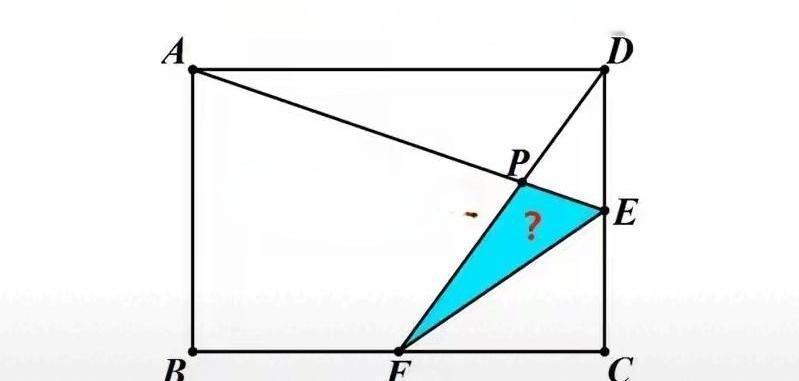
一道看着不起眼的几何题，矩形面积160，求里面一个被线段切割出来的小三角形面积。 这题能把人直接绕进去，很多人上来就想用坐标系，设一堆未知数，最后把自己算得头昏脑涨。 其实这根本不是考计算的，而是考思维的巧妙。 高手解这种题，根本不直接去算那个小三角形。他们会先用“割补法”，把整个矩形面积160，减去周围三个明明白白的直角三角形，它们的面积分别是40、20、40。这么一减，中间那个大一点的三角形AEF面积就出来了，是60。 接下来才是最关键的一步，也是区分普通人和高手的环节。通过构造相似三角形，可以轻松证明出长线段AE被P点分成了4:1的两段。这个比例关系一出来，问题就迎刃而解了。 既然大三角形AEF的面积是60，而目标小三角形PEF和它共用一个顶点F，底边PE又正好是AE的五分之一，那面积自然也是大三角形的五分之一。 60乘以五分之一，答案12，干脆利落。 非要去建坐标系硬算，虽然也能算出12，但那种几何的美感和智慧的乐趣就荡然无存了，纯粹是把数学题变成了体力活。 这题考的，从来不是计算能力，而是脑子会不会转弯。