
函数有多种表现形式,同样一个函数,可以通过抽象的数学表达式进行描述;也可以通过直观的函数图像进行描述。就像“正弦函数y=sinx” ,可以根据函数解析式进行相关计算,同时也可以根据函数图像直观得出单调性和最值等信息。
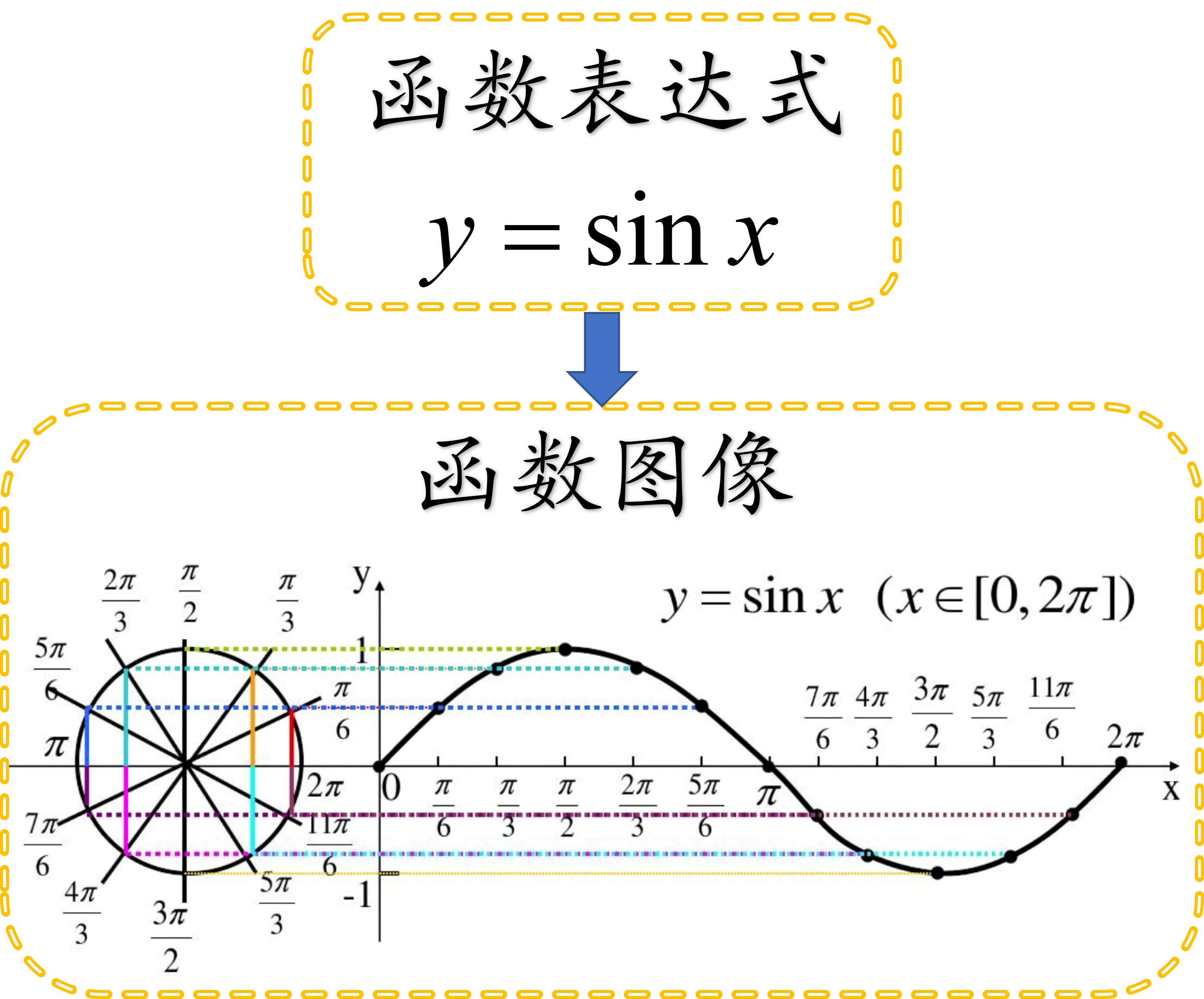
三角函数的图像性质在做题过程中会帮助我们更好地解题,我们学习的都是最基础,最简洁的函数形式。正弦函数就像是最基本的原材料,经过函数的伸缩和平移变换就会孕育出各种各样的函数曲线。
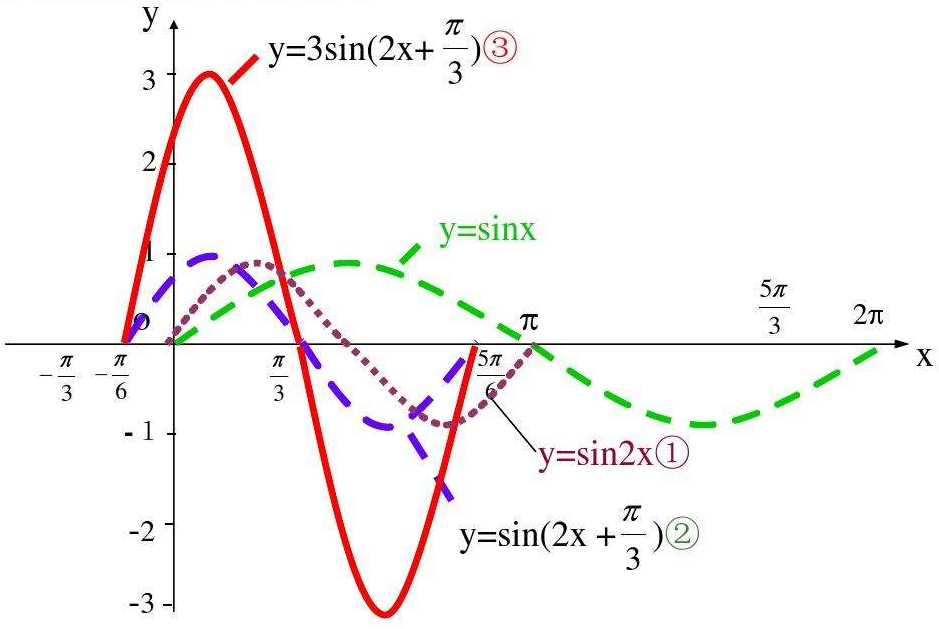
本期分享的例题主要展示三角函数的伸缩平移变换,考察三角函数的图像性质,包括对称轴、周期,最值等信息,同时这道题目对于三角函数图像的伸缩和平移变换也是考察的比较深入。当然这道题目也是有一些难度的。希望这道三角函数题目能帮大家回忆相关的知识点,题目只是一个工具,核心还是我们的基本功!


对于这一类题目,尝试使用数形结合的数学思想方法进行处理的话,思路会比较清晰,也比较好理解。简单说“要想有前途,就要多画图”。
这道题目核心考察三角函数的伸缩平移变换,从最简单的正弦函数到题目给定的函数。伸缩平移变换过程中相应的点的坐标也会发生对应的改变!
在分析的过程中,我们先从正弦函数出发,将函数变换的步骤拆解,可以初步得到函数f(x)的图像,然后再结合题目给定的条件,基于函数图像进行分析,得出相应的不等式约束,求解之后就是最终的采纳数取值范围。总体难度有点大,分析过程中要注意理清思路。
这道三角函数题目能很好地帮大家回忆函数变换的知识点,是一道非常不错的题目,值得反复研读。