
今天我们讲遇到角平分线,做辅助线的3种方式
01
看到角平分线该想到什么
看到角平分线该想到什么?
首先,角平分线把一个角分成相等的两份。其次,角平分线的尺规作图方法。好,我们回顾一下角平分线的做法6。
(这里我们只说标准作法,也是教科书上的方法)
1. 以角的顶点为圆心,任意长度为半径画弧,分别交角的两边于点A和点B。
2. 分别以点A和点B为圆心,以大于线段AB一半的长度为半径画弧,两弧在角的内部相交于点C。
3. 连接角的顶点和点C,这条射线即为角平分线。
看到这样的做图方式,你就要想到:
做的是角平分线。
因为很多题目都是这样考察的,比如下图这道。

接着说:还有呢?还需要想到什么?
角平分线到角两边的距离相等。
这是做图延伸出来的,为什么我们做出的就是角平分线呢?
因为构成了全等三角形。
连接AC、BC,△OAC全等于△OBC.
同样的,我们做垂线也能构成全等三角形(如下图)。

这就引出了第一种做辅助线的方法:从角平分线往角的两边作垂线。
02
作垂线
如下面这一题。

这道题没有直接告诉学生AD是角平分线,只讲了它是如何做出来的——
很明显,考察你对尺规作图熟不熟悉。
熟悉了,就知道做出的AD是角平分线。
现在求CD的长。
CD的长并不好求,但我们做个辅助线——
作DE垂直AB于E点。
把求CD的长转移成求DE。
我们设DE=x。
利用勾股定理,找到一组等量关系,再解方程就可以了。

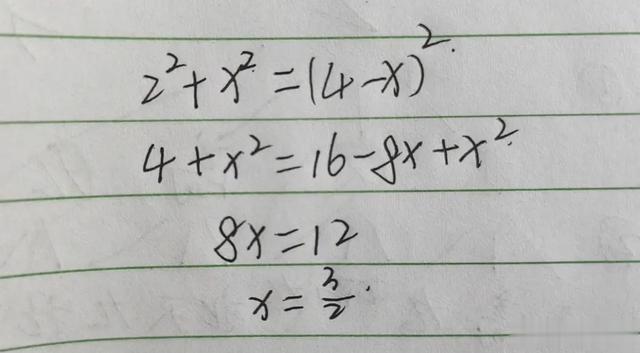
在这里,垂线段DE起到了关键的作用。
所以,遇到角平分线,你不妨往垂线段上想想。
除此之外,你还可以往平行线上想一想。
03
做平行线
做平行线也有特殊效果。
因为平行的时候,内错角相等、这样就可以构成等腰三角形。
等腰三角形在解决全等、长度、角度等问题上,很有帮助。
看2个例题(解答已经写上去了)。

这两个题目都利用了角平分线上一点向角的一边做平行线,利用内错角相等,构成等腰三角形,来解决问题。
所以,遇到这种求比值、求线段相等的题目,都可以试试平行线。
即便有时候不那么明显,那你也要试试在不同的地方做平行线。
比如下面这道题。

04
做等线段,构成全等三角形
可以利用角平分线平分一个角,再截取相等线段来构成全等三角形。
这样也会得到一些特殊关系。
这种方法在下面这个题目中体现得很完全。
它一步步地教我们如何截取相等、如何构造全等三角形。
仔细看看题目,其他的我就不多说了。

05
利用三点共线,构造等腰三角形
有一种题型,从角边上一点作了角平分线的垂线。
此时垂足和这个点在一条线上,把这条线延长交另外一边一个点。
三个点共线,我们也找到一对全等三角形,而作为一个大三角形,它是等腰的。
如图。

这种题目的辩识性很强,是很容易做出辅助线的那种。
好,遇到垂直平分线怎样作辅助线我们就说完了。
一共总结了4种:
垂直平行线做等线段三点共线记好了,遇到角平分线,问题比较难,看起来不容易解决,就试试这些辅助线。
本文结束,谢谢阅读。