接上篇。

7.对潮汐的解释。

潮汐现象一直很神秘。有人猜测潮汐与月亮有关。但是究竟是什么关系？没人能说清。

有些人则认为，月亮引起潮汐的想法是无稽之谈。比如，近代科学的奠基人伽利略，就嘲笑了这种想法。

伽利略花了许多心血，提出一种对潮汐成因的解释。他对他的潮汐理论很得意。但他的理论其实是错的。

牛顿表明，潮汐是由月亮对海水的吸引力（万有引力）的差异引起的。

理解这一点不是那么容易的。解释清楚其中的推理，也不是本文的重点。

这里只指出理解这问题的关键，即：地球与月球之间的吸引力，使得二者围绕一个共同的中心运转。这个中心点位于地球内部，地面下大约1000英里的地方。

海水跟随地球，也绕这个中心转动，而这需要向心力。

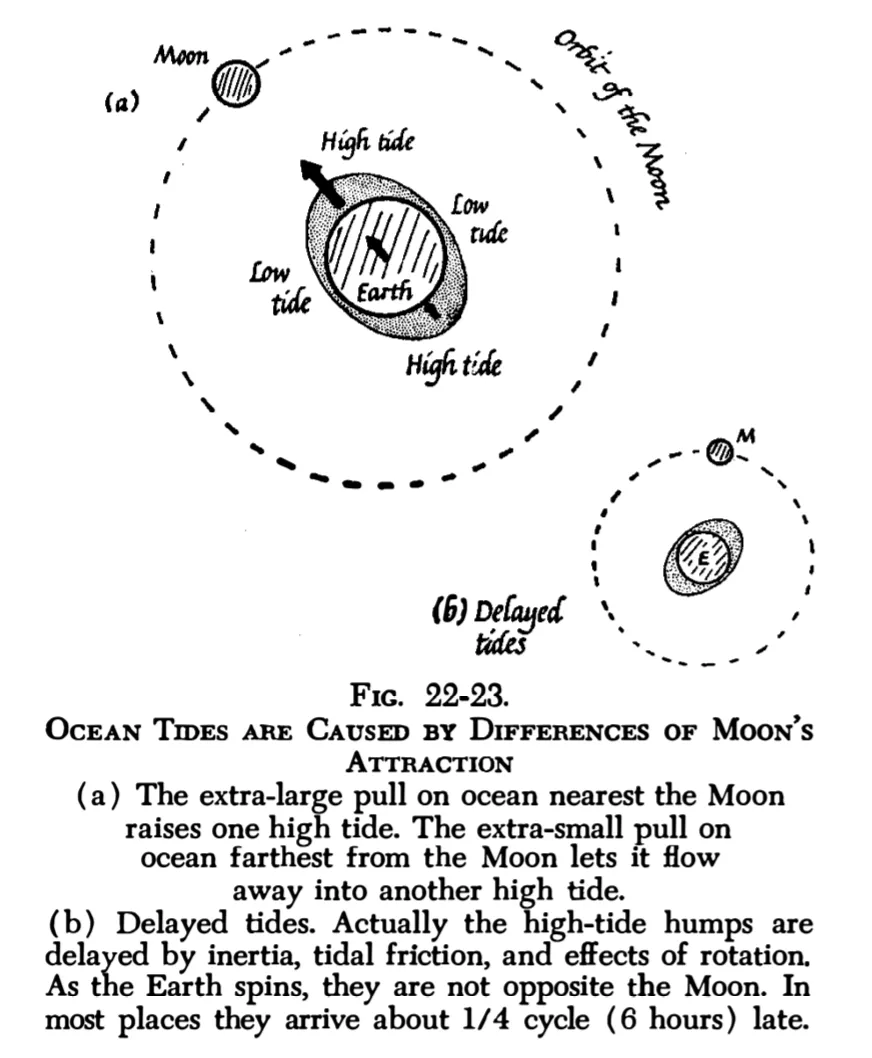
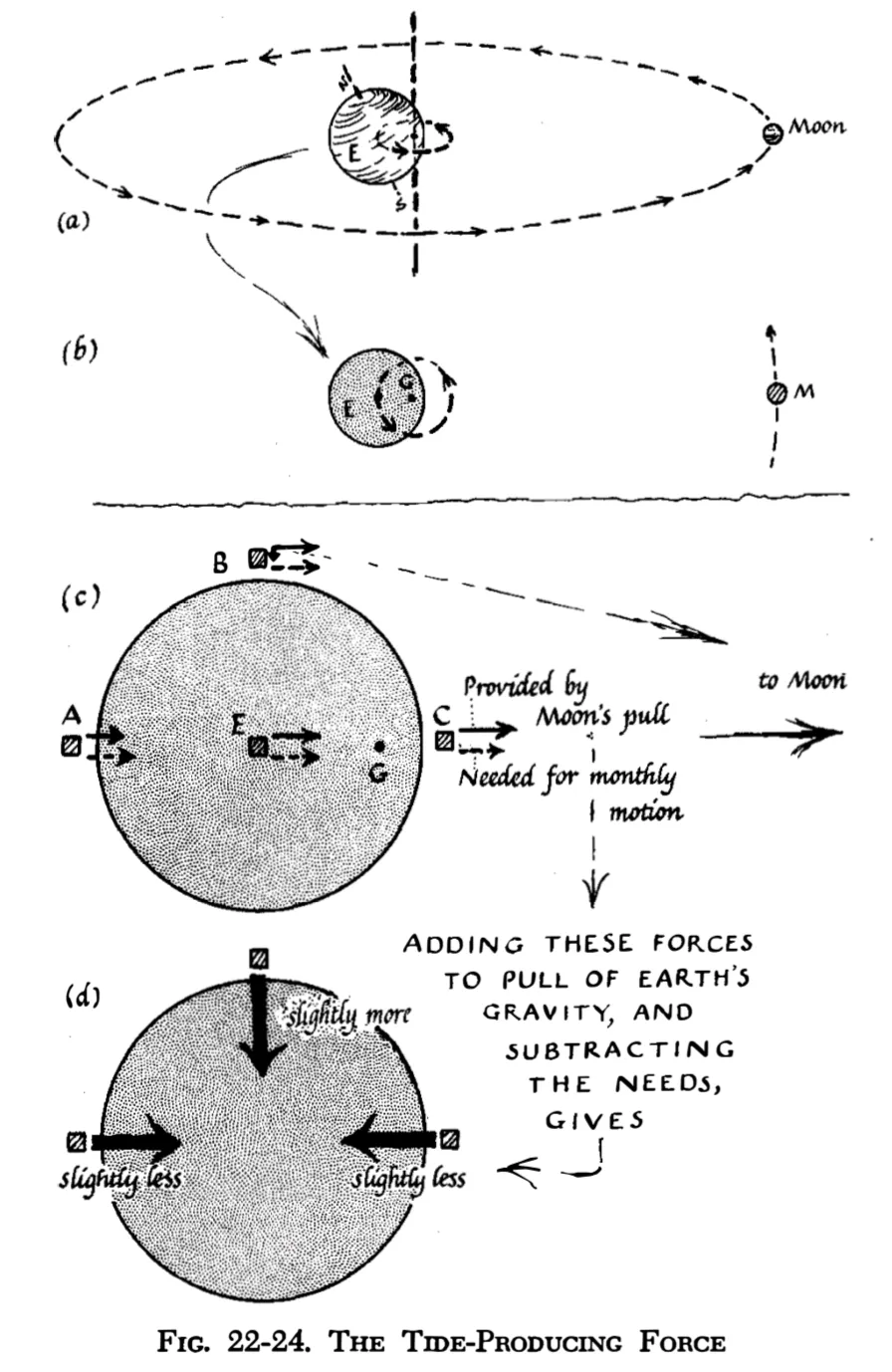
朝向月亮的那部分海水，由于离月亮比较近，月亮的吸引力超过海水所需的向心力。背向月亮的那部分海水，由于离月亮比较远，月亮的吸引力小于海水所需的向心力。

最后的结果是，朝向月亮与背向月亮的海水的“重量”，都显得比正常值小一些。于是，这两部分的海水会稍稍鼓起来。

（由于惯性和摩擦力，水面最高的地方不是正对和背向月亮的地方。）

海水不但受到月亮的吸引，还受到太阳的吸引。两种吸引力的效果，每月会有两次重合，这时潮汐的幅度会最大，叫做大潮。大潮之间的日子是小潮。

8.计算月球质量（为地球质量的多少倍）。

根据月球绕着地球转动，地球（或其它行星）绕着太阳转动，木星的卫星绕着木星转动等等，牛顿可以算出各中心天体（地球，太阳，木星等）质量之间的倍数关系。（算不出它们是多少千克，因为那时候还不知道万有引力常数的值）

可是月球没有它的“卫星”。所以，本来无法算出，月球质量与地球质量之间的倍数关系。

可是牛顿真地是天纵之才，他通过比较大潮与小潮的差异，把太阳与月球对潮汐的效果分离出来，算出了，只受月球吸引时的潮水高度。

根据这个高度，牛顿可以算出月球质量与地球质量之间的倍数（海潮相当于月球的卫星）。

9.对彗星的解释。

彗星是什么？亚里士多德认为彗星不是天体，而只是云里的蒸汽（不是天文现象，而是气象现象）。

第谷和开普勒证明了，彗星要穿越行星轨道，因此不可能是云里的蒸汽。

但是他们认为，彗星只会拜访太阳一次，然后再也不会重来。

牛顿证明了，彗星像别的行星一样，也是沿着椭圆轨道运动，太阳在椭圆的一个焦点上。只不过，行星的椭圆轨道与圆很接近，而彗星的轨道是很扁的椭圆。

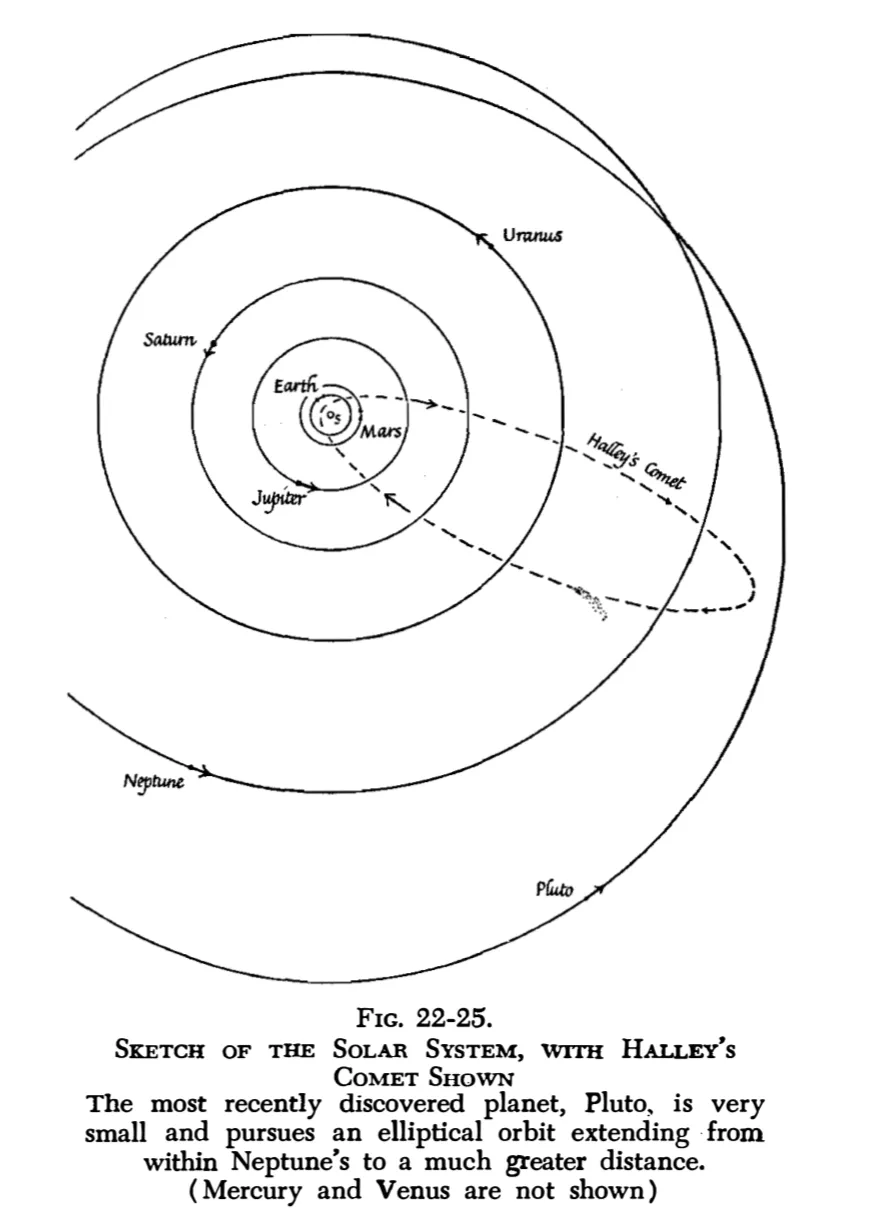
当彗星出现时，记录下它出现期间的运行路线，可以推算出它的整个椭圆轨道（老贾：这个也很难），并可预测出它下一次重新出现的时间。

确实也有一些彗星，只拜访太阳系一次。这种彗星的轨道不是椭圆，而是双曲线。牛顿的理论也包含了这种彗星。

篇幅差不多了，后面3个成果，我只简略介绍一下（这不代表它们不重要。实际上，最后一个成果，可说是牛顿最伟大成果）。

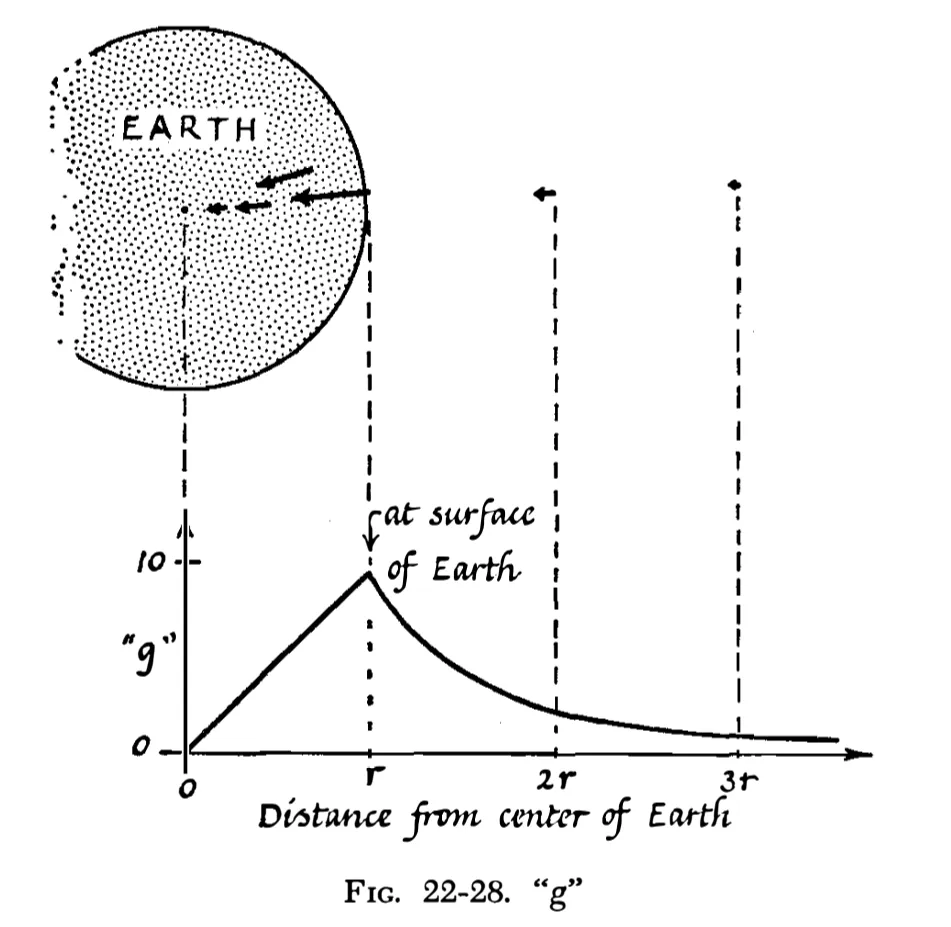
10.物体在地球内部时的重量。

牛顿在这方面的研究，对后来静电学的发展很重要。

11. 人造卫星的设想。

月亮是地球的卫星。牛顿指出，当我们抛出一个石块时，这个石块就成为地球的一个卫星，它与月球一样，沿着椭圆（没错，是椭圆而不是抛物线）轨道绕地球运行。

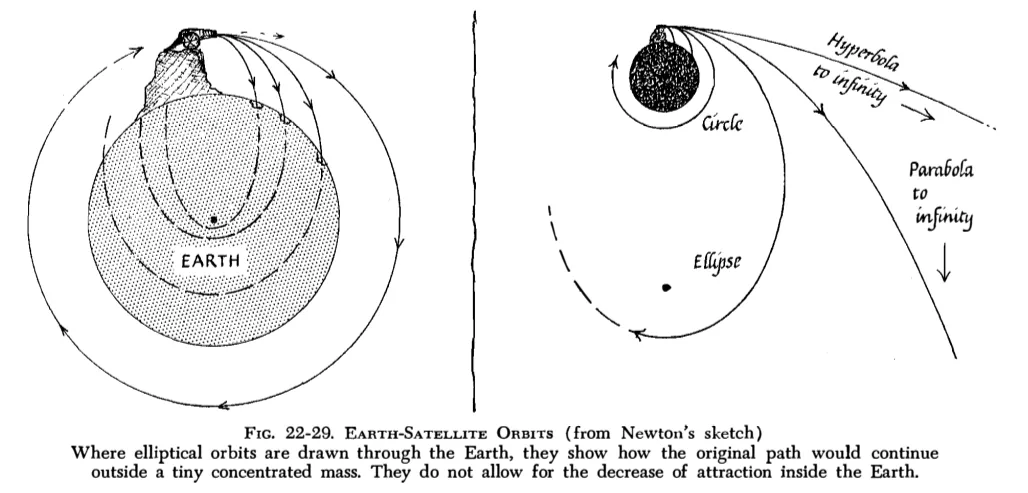
如果石块的速度足够大，就会绕地球运行，而不掉下来。

如果速度继续变大，石块会脱离地球，永远不再回来。

12. 行星的摄动。

牛顿根据月球绕地球的转动，以及开普勒的行星三定律，猜出了万有引力。可是，假如他猜的是对的，那么，行星不但受到太阳的吸引，而且还要受到其它行星的吸引。

这样一来，行星的轨道就不会是简单的椭圆，而会有许多复杂的变动。

这样一来，行星的运动不可能严格遵守开普勒定律。开普勒定律只是近似成立。

这个计算难极了。但是我们的（或者他们的？）牛顿没有被吓住。

他计算了木星对土星运动的影响（你猜他为什么要这样选？）。

结果表明：他算出的土星运动的细小不规则性，与天文学家们的观测结果一致！