文/福星徕
编辑/福星徕
前言
数值方法作为一种分析粘弹性流体行为的重要工具,为研究人员提供了一种有效的手段来分析和预测其复杂的流动特性。
常用的数值方法,如有限元法、有限体积法和格子玻尔兹曼方法,以及它们在模拟粘弹性流体行为方面的适用性。如何选择适当的数值方法来解决特定问题,成为数据分析的重中之重。

粘弹性流体的数值方法
复杂流体流动问题的数值模拟最初是在70年代初开始的,当时借鉴了当时已知的数值方法来求解控制着不可压缩纽维尔流体流动的纽维尔-斯托克斯方程。
从那时起,基于有限元方法或标准有限差分方法的离散形式就被开发出来。特别是对于具有应变速率相关黏度(流变恒稳或流变变稠行为)的非纽维尔流体,提出了精确的离散形式。
然而,由于数学形式仅适用于不包含诸如法向应力差异效应等现象的非弹性流体,所使用的方法对于精确模拟粘弹性流体行为的流变模型并不具有实际意义。

对于由Rivlin-Ericksen粘弹性理论推导的流变模型,在弱弹性流体的假设下,也开发了由CEF模型描述的粘弹性行为的数值模型。在此背景下提出的技术也有助于粘弹性流体问题的数值建模,其流变行为由Oldroyd类微分方程给出。
这是因为有限差分和有限元等离散化方法最初是为求解椭圆型EDP而设计的,对于对流扩散问题,特别是在粘弹性流动和弹性效应占主导地位的情况下,传统的离散化方法可能变得不稳定,因此与解决由诸如Oldroyd-B,Giesekus或PTT的模型流变描述的粘弹性流体的问题无关。
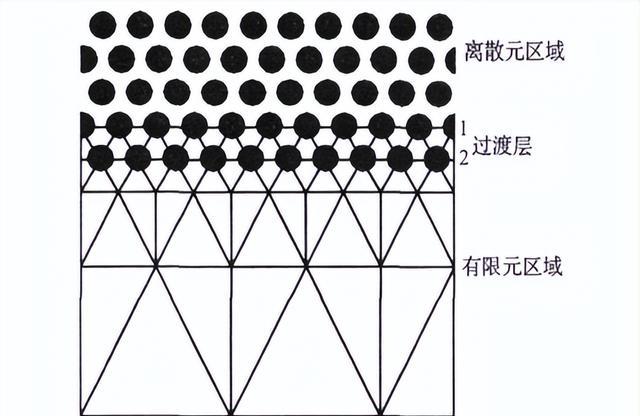
在80年代初,科学界认识到高韦氏数问题是在非平凡几何体中进行粘弹性流体流动数值模拟的主要困难,特别是针对UCM、Oldroyd-B等类型的粘弹性流体。
高韦氏数问题表现为当空间分辨率加细时,迭代方法无法收敛的现象,特别是在韦氏数适度偏高的情况下。最大韦氏数取决于空间分辨率,在大多数数值方法中,随着网格加细,最大韦氏数下降得更加剧烈。
与数值工具的收敛性丧失相关的困难被归因于几个原因,包括使用不恰当的本构方程、数值方案无法正确处理解在奇异点附近的陡峭梯度,或者边界条件的错误规定。迄今为止,这种不稳定机制的起源仍然是未知的。

尽管在不同尺度上,这些元素或多或少是推测性的,但将数值困难的起源归结为在数学结构上使用了不恰当的数值近似,这是由于在理论(分析)层面上不存在限制所导致的。
最常在经典基准测试中出现高韦氏数问题的有:4:1收缩通道中的流动问题,驱动腔流动问题,圆柱周围的流动问题以及时间依赖的Poiseuille流动问题。对于这些,只有在韦氏数较低的情况下才能获得稳定和收敛的数值解。
Oldroyd-B流体在稳态Stokes流动中可以导致系统方程类型的改变,类比于可压缩流动,在流体速度超过声速时,系统方程从椭圆型变为双曲型(当马赫数增大时),将弹性马赫数视为决定Stokes流体的稳态流动中方程类型变化的参数。

并据此提出了一种上风型方法,在超临界状态(Ma>1)下,即在发生类型变化时,近似控制方程组。在与流体局部速度和法向应力状态有关的某些条件下,稳态涡度方程可经历由椭圆型向双曲型的方程类型转变。这种情况导致进化的损失(哈达玛不稳定性),随着空间分辨率的增加,进化变得越来越严重。
因此,对于处于斯托克斯流(无惯性)中的UCM流体,Renardy表明,在这种配置下不可能发生类型变化,这表明与传统数值格式观察到的收敛性损失是由于导致人为(数值)类型变化的误差。
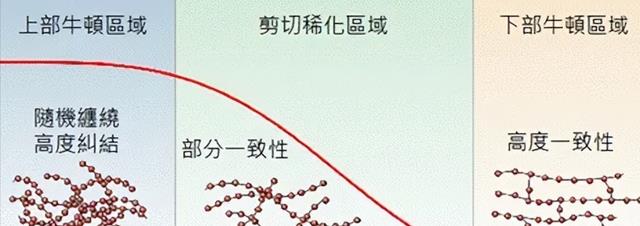
Oldroyd类的流变模型的双曲性质要求使用适合问题性质的离散化技术,在这个框架下,已经发展了许多稳定化方法,以抑制干扰振荡。例如首次应用于Oldroyd-B本构模型描述的粘弹性流动的SUPG(Streamline-UpwindPetrovGalerkin)方法。
在本构方程中没有扩散项的情况下,这些变分公式通常在流体弹性较大时遇到困难,特别是在UCM流体的情况下。
根据流动配置(收缩流动,驱动腔流动)模型来说,粘弹性效应主导了由牛顿贡献引起的粘性效应,从而产生了数值上的干扰不稳定性。事实上,对于动量方程来说,粘性项的贡献越重要,优于聚合物贡献,数值方法的性能就越好。
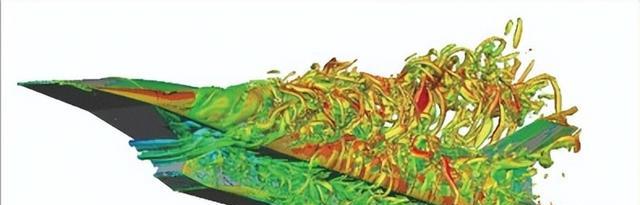
在动量方程中,如果粘性项的贡献相对于聚合物贡献更为重要,数值方法的性能就会更好。因此,为了稳定数值解,一些提出的技术旨在增加动量方程的椭圆性,将问题转化为椭圆型问题。
例如,EVSS(弹性-粘性应力分裂)公式、DEVSS(离散弹性-粘性应力分裂)公式和DEVSS-G方法是一种DEVSS公式的变体。EVSS公式通过与聚合物应力张量Σ=τ?2(1?β)D相关的变量变换来实现。
通过这种变量变换(EVSS)来引入额外的椭圆性概念到动量方程中,并在之后扩展到粘弹性流体中。
这种方法的优点在于扩散算子可以将方程组简化为Poisson问题的形式,然而,这种公式的主要缺点在于需要计算应变率张量的上对流导数,这意味着需要对速度向量的分量进行二阶导数的近似。
此外,使用投影(分数)方法来处理额外的未知数,即应变率张量或速度梯度张量,配合EVSS-G方法,将其作为单独的变量处理。然而,EVSS方法所依赖的变量转换只适用于某些类型的本构方程。
为了增加本构方程和动量方程的椭圆性,并避免对模型进行转换,提出了DEVSS(DiscretEVSS)方法。

该方法通过以离散方式在动量方程中添加和减去两个在不同时间级别评估的相同粘性贡献的数值近似来引入粘性项。因此,包含在总应力张量中的离散应变率张量通过投影方法进行近似,并作为额外的变量进行处理。
DEVSS-G方法使用了在本构方程中作为额外未知数的速度梯度张量,而不是应变率张量。然而,尽管经过这些处理,本构模型的方程类型仍然是双曲型的,这需要使用其他稳定化方法。此外,由于额外项的引入会破坏瞬态解,这些方法不适用于瞬态问题。
BDS(Both-SidesDiffusion)方法类似于DEVSS方法,在有限体积法中是最常用的稳定化方法。BDS方法是通过在本构方程的两侧添加人工扩散项并选择满足对角占优条件的人工扩散系数来实现的。
本构方程采用经典的有限体积法进行离散化,左侧添加的额外项以隐式方式近似处理,而右侧添加的额外项以显式方式近似处理。这种方法的缺点是会干扰瞬态解,只有稳态解满足初始方程组的条件。
然而,在三维4:1的收缩流中成功获得了具有Weissenberg数(We)小于等于4.6的Oldroyd-B流体的稳定和收敛结果。在有限体积法中,采用半拉格朗日方法解决了Oldroyd-B流体在收缩道中的流动问题。
对于Deborah数(De)小于等于2.5的情况,获得了稳定和收敛的结果。这种方法的局限性被证明是由于需要加大网格分辨率以捕捉粘弹性应力张量分量的突变变化。
因此,采用了一种完全隐式的基于有限元方法的算法,并使用CUBISTA(平流处理的收敛和普遍有界插值方案)分别处理出现在动量方程和本构方程中的对流项。成功地获得了Oldroyd-B流体在收缩通道中斯托克斯流动的收敛解,对应的Deborah数(De)小于等于3。

在结合了有限元法处理复杂几何形状的优势和有限体积法满足物理量守恒原理的优势的基础上,还开发了其他混合方法。在这方面,提出了一种混合处理方法,其中使用有限元法处理动量方程,而使用有限体积法处理本构方程。
对流项通过满足总变差减小(TVD)条件的通量校正对流方案进行离散化。另一种基于有限元法/有限体积法的混合方法被提出,用于解决Oldroyd-B流体在四倍收缩比的流动中所遵循的方程系统。
动量方程采用有限元法处理,而Oldroyd-B模型则采用有限体积法处理。与传统有限元法相比,这种方法显著改善了数值预测,并获得了稳定和收敛的稳态解,适用于Weissenberg数(De)小于等于4的情况。

对于较高的Weissenberg数,稳定性的丧失是由于在奇异点附近应力张量梯度的显著增长所致,建议在奇异点处细化网格。在控制Oldroyd-B模型相关的不可压缩流动问题的方程系统类型方面,最早进行了分类。无论是关于时间依赖的流动还是定常流动,都强调了考虑控制方程系统的类型的重要性。
事实上,这些导致了许多解算算法的产生,其中考虑了控制方程系统的混合类型(椭圆-抛物-双曲)。针对这类混合类型方程的数值方法并不是很成熟,离散化的困难主要与对流项的处理不当有关。

离散误差的积累可能导致构型张量正性特性的改变,尽管在连续级别上构型张量是定义为正的。构型张量正性特性的丧失可能导致数值不稳定,使得方程系统不再是演化型的。
LCR(Log-ConformationRepresentation)方法可以明确避免构型张量的正定特性受到破坏。Fattal和Kupferman首先指出,数值困难的一个方面可能与基于多项式逼近的数值方案无法准确再现由包含在上导数中的变形项引起的聚合物应力的陡峭指数增长有关。
当变形速率变得足够大,超过了导数项中的对流和弛豫项时,会发生数值不稳定。这种不稳定性在所有满足Oldroyd参考系不变性原则的标准数值方法中都存在,并且适用于所有满足Oldroyd参考系不变性原则的构型模型。
LCR方法实际上是基于一种变量变换的思想,该变量变换将构型张量(对称且正定)对数对角化,以预测粘弹性应力张量的指数行为。其主要思想是基于这样一个观察:基于多项式逼近的数值方法无法捕捉构型张量的指数增长,但可以捕捉其对数的多项式变化。
在4:1收缩的情况下,已获得了Weissenberg数大于等于3的稳定且收敛的结果,作者建议使用更细的网格以提高算法的稳定性。该方法已在多项数值中使用。该变换的主要优点是在离散水平上自然保持构型张量的正定性。然而,由于出现了Weissenberg数的倒数,该公式在Weissenberg数趋近零时会变得奇异并发散。
为了解决这个问题,提出了各种不同的改进方法,如强根构型张量因子分解方法(SRCR,Square-Root-ConformationRepresentation)。最近在有限体积方法中,他们使用了CUBISTA方案来近似构型张量对数的对流方程。
另外,一种适用于仿射粘弹性模型和非仿射模型的可调节形式,使得当Weissenberg数趋近于零时,椭圆-抛物-双曲控制方程系统能够恢复到Navier-Stokes方程。

在有限差分方法的背景下,开发了一个纯粹双向波动的二维数值算法,用于具有溶剂粘度在总粘度中的比值为零的Giesekus流体的时间相关、弱可压缩流动。通过允许低度可压缩性,控制方程系统在准线性形式下从椭圆-双曲型变成纯双曲型,从而允许应用特定于双曲型问题的数值方法。
开发的算法更好地处理了控制方程系统的完全双曲性质,并在驱动腔体基准测试中,对于Deborah数小于等于4,获得了稳定且收敛的结果,该方法的局限性与计算成本过高有关。

为了解决在收缩通道中不可压缩Oldroyd-B流体的双曲型控制方程系统,Trebotich等人将构型方程重新写成一种形式,使得在离散水平上可以分别恢复聚合物应力张量在松弛时间趋近于零和趋近于无穷时的纯粘弹性和纯弹性极限。
对于Oldroyd-B方程,采用了一种分数阶方法,其中对流项使用Lax-Wendroff方法进行离散化。基于有限差分的方法,所提出的实现使用分数阶投影方法(预测-校正法)来施加不可压缩约束。
对于时间相关的解,当马赫-弹性数(Ma<1)处于亚临界范围时,获得了稳定收敛的结果,其中任意Weissenberg数的值均可。认为这种对马赫-弹性数的限制是由于在对流项中使用Lax-Wendroff格式的结果,并建议使用Upwind方法来处理可能出现的不连续性。

作为对工作的延伸,提出了以准线性形式重写控制方程系统的方法,然后引入了一个控制方程系统的保守形式。
基于有限差分法,为了捕捉弹性波的传播,采用了二阶Godunov方法对超波部分进行离散化,以取代Lax-Wendroff方法,从而显著放松了CFL数。该方案对于Oldroyd-B流体在复杂的二维几何形状中具有二阶收敛性。

保守形式应用于多模式的Giesekus流体流动,控制方程系统的超波部分采用二阶Godunov方法处理。
这种基于混合方法(有限元/有限差分)的公式,利用牛顿-拉弗森线性化方法用于Giesekus流体的可压缩流动。据指出,边界上的边界条件的数量和类型可以根据进出特征变量使用特征线方法明确确定。
根据这个综述,数字处理这个问题的复杂性变得明显,因为大多数算法都是针对同一类型的方程系统设计的。而控制粘弹性流体流动的方程属于混合类型。此外,在高Weissenberg数值下,正确处理超波部分是确保稳定和收敛的数值方法所必需的。

基于经典的有限差分方法,这种数字方法可以正确处理控制方程系统的超波部分,并在离散尺度上保持构型张量的对称和正定性质。
在时间上,采用Euler格式的一组与其他项半隐式处理相结合的方法,这在求解不可压缩Navier-Stokes方程时很常见。在空间上,方程的准线性部分采用适当高阶非中心格式进行离散化,而其他项则采用二阶中心格式进行近似。

结论
粘弹性流体的数值方法应用在生活的方方面面,无论是在工程领域、生物医学领域、环境科学中,甚至是模拟地下水的流动、土壤污染物的迁移和地震引起的地下水位变化等都有重要作用。通过对粘弹性流体行为的数值模拟,可以更好地理解和管理环境系统,为环境保护和灾害预防工作提供支持。
尽管粘弹性流体的数值方法已经取得了重要进展,但仍面临一些挑战。其中之一是模型参数的选择和测量的不确定性,这会对数值模拟的准确性和可靠性产生影响。
粘弹性流体的多尺度性质使得数值模拟变得复杂和耗时,因此,改进数值方法的精度和效率、提高模型参数的测量精度,并开发适用于高性能计算平台的并行化算法成为当下最亟需解决的问题。
只有不断改进和发展数值方法,能够更好地理解和控制粘弹性流体的行为,进而推动相关领域的科学发展和技术创新。