今天我们讲函数求值域

求函数值域不算一个大知识点，通常会是一个小题目。

选择题或填空题，一题5分。

或是一个大题的第一问，差不多5分。

这5分相对来说好拿。

下面我们做个题型总结，多看几遍，这5分你就拿到手了。

01

分离常数法

这是最简单的一种方法——适用于自变量是一次的分式函数。

我们看到这样的分式函数，就通过配方，把它变成一个常数+一个分式的样子。

它的值域就显而易见了——≠常数。

02

配方法

如果你遇到的是一个二次函数，可以用配方的方法。

这个方法在初中就已经非常常见了。

把未知数配成完全平方的形式。

完全平方≥0，那么值域就显而易见了。

配完全平方要注意：

常数项是一次项系数的½。

前面加上了一个常数，后面就要减去。

03

换元法

换元法又分代数换元和三角换元。

它们的使用场景都是含有根式的函数。

代数换元是普通根式函数；

三角换元是比较“巧”的根式函数。

代数换元的例子。

代数换元是把根式里的“一堆”设为t，

然后两边平方，转换成二次函数，

再配方求值域。

三角换元法例子。

三角换元法适合根式下是【平方差】的函数。

根式下是平方差，我们就可以利用正弦余弦平方相加为0。

然后令自变量＝三角函数，来进行变换。

最后利用三角函数值来确定函数值域。

04

判别式法

这个方法也很巧妙。

适合分式函数，且分母次数为2次的分式函数。

遇到这种情况，我们可以把分式转化为一个二次方程。

在这个方程里，用y做系数，x依旧是自变量。

那么，方程要有根，判别式必须≥0。

这样y的值，也就是值域也就计算出来了。

注意，要讨论二次项系数，系数≠0。

其实这也叫反函数法——用y表示x嘛。

假如再遇到分式函数，不想配方也行。

我们可以用y表示x。

然后再判断值域。

05

基本不等式法

基本不等式你还记得吗？

a+b≥2√ab

如果一个函数是y＝x+1/x-4

那么对于前半部分你就可以用基本不等式。

x+1/x≥2

当x=1/x，也就是x＝±1时，成立。

函数的值域也可以求了。

如果一个函数不是x+1/x的形式，你就给它化简成这样的形式。

比如下图中的这些。

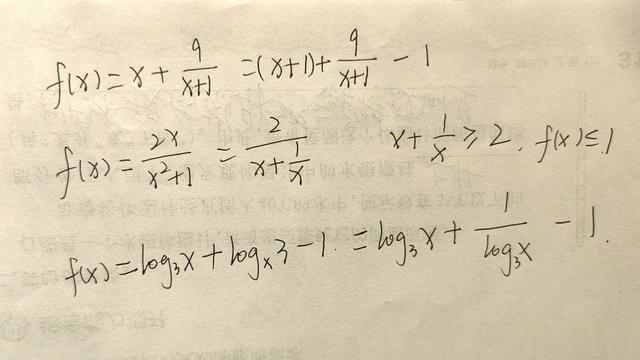
06

导数法

求函数的导数，让导数等于0。

此时的自变量取值，对应的就是函数的极值。

这个方法我以前讲过。拓展阅读链接在下方。

两种函数求极值的方法：一种是理想，一种是现实

07

比例法

适合结合一次函数的复合函数。

先把x和y写在等号两边。

然后让等号两边等比例，设为k。

用k表示x、y，代入复合函数来判定值域。

08

利用函数基本性质

函数有单调性、奇偶性、有界性等性质。

只要你熟知各个函数的特征，有时候单是观察复合函数，就能知道值域。

很多人管这个方法叫观察法，根本上还是根据函数的特点。

还有图形结合，也是根据函数本身。

只要把函数图像画出来，那么函数的值域也就一目了然了。

我们还可以利用函数的有界性。

比如，三角函数，二次函数，指数函数等。

它们的值域都在一定范围内。

一个复合函数包含这些初等函数，利用有界性判断一下就行了。

比如下面这些：

利用函数的单调性，也是一个非常好的方法。

调函数的图像是一直上升或下降的。

单调函数在端点处有意义，则该函数在单点处取最值。

比如：

一个函数在[2,8]上单调递增，则在2上取最小值，在8上取最大值。

一个函数在[2,8]上单调递减，则在2上取最大值，在8上取最小值。

好了，基本上都总结完了。

具体的你再到题目中去试试。

不练肯定不行。

本文结束，谢谢阅读。