各位朋友,大家好!“数学视窗”这次依然给大家分享一道数学竞赛题,这是一道求图形面积的问题,大多数学生看到这道题都是无法动笔,此题难度之大是可想而知的,主要是没有解题的思路,不知道从何处开始!下面,我们就一起来看看这道例题吧!
例题:(数学竞赛题)如图是由外围的一个大正方形和内部的两个长方形拼成的对称图形,已知阴影部分的周长为36厘米,线段AB的长度为2厘米,那么大正方形的面积是( )平方厘米。
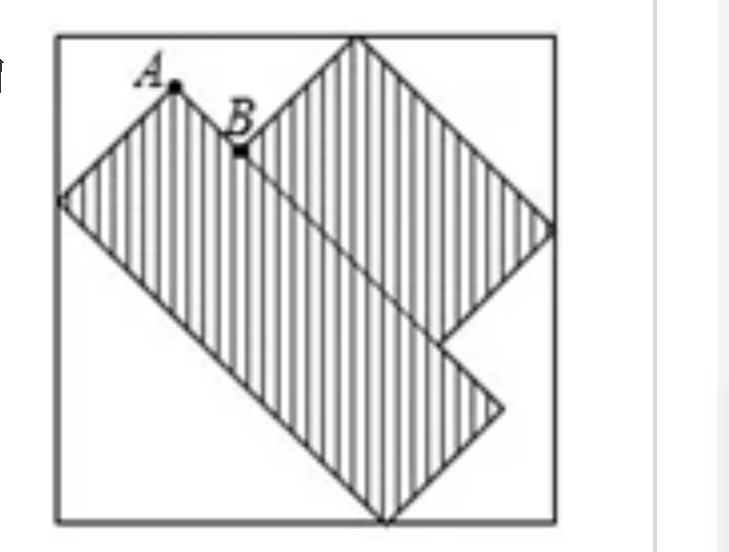
分析:此题中所给出的条件非常有限,仅仅指出了一个大正方形和两个长方形,以及给出了两个长度数据。题目要求出大正方形的面积,一般是想办法求出边长,但是题中没有任何相关的条件。那么,我们如何进行转化,进而求出面积呢?
其实,题中还有一个重要条件没有使用,那就是拼成的是一个对称图形。既然是对称图形,而图中又有正方形,则其中的隐含条件是非常多的。
根据阴影部分的周长为36厘米,可以先把相关线段作一定的延长和移动(如图),然后再利用正方形的对称性,计算出正方形对角线的长度,最后利用正方形对角线可以算出正方形的面积,即可解决问题。

解法:如图,橘色线段围成的图形周长与阴影部分周长相等,
因为图中正方形的一条对角线就是对称轴,
所以图中橘色线段的长度和为
36÷2=18(厘米),
如图,再画出另一条对角线,
可以推出橘色对角线上方的线段比下方的线段总长度多2厘米,
所以DE+EF=(18-2)÷2=8(厘米),
又DE=OF,EF是等腰直角三角形的一条直角边,
所以对角线长度是2(OF+EF)=16(厘米),
所以正方形的面积是
1/2 ×16×16=128(平方厘米)
故正方形的面积是128平方厘米.
(完毕)
这道题主要考查了线段之间的平移与图形的对称性,解答此题的关键是进行线段平移,并结合图形的对称性进行解答,此题是一道巧题,难度较大,需要较强的发散性思维。温馨提示:朋友们如果有不明白之处或者有更好的解题方法,欢迎大家给“数学视窗”留言或者参与讨论。
评论列表