在串联电路中，电流处处相等的特性，是电路理论中一个基本且重要的概念。

这一现象背后的原因，不仅涉及电流的定义和性质，还与电荷守恒定律、欧姆定律以及能量守恒定律等物理规律紧密相关。

从电流的定义出发，电流是单位时间内通过导体横截面的电荷量。

在串联电路中，由于所有元件（如电阻、电容、电感等）依次连接在同一条路径上，因此在任何时刻，通过每一元件的电荷量必然相同。

这意味着，如果在一个串联电路中，某一位置的电流为I，那么经过电路中的每一个其他部分的电流也将是I，因为通过它们的电荷量必须保持一致。

进一步地，电荷守恒定律也支持了上述观点。

该定律指出，在一个孤立系统中，电荷的总量保持不变。

在闭合的串联电路中，没有额外的电荷注入或流失，因此流入任何一个元件的电荷量等于流出的电荷量。

由于整个串联电路是一个闭合的系统，所以在整个电路中流动的总电荷量是恒定的，这直接导致了串联电路中电流的一致性。

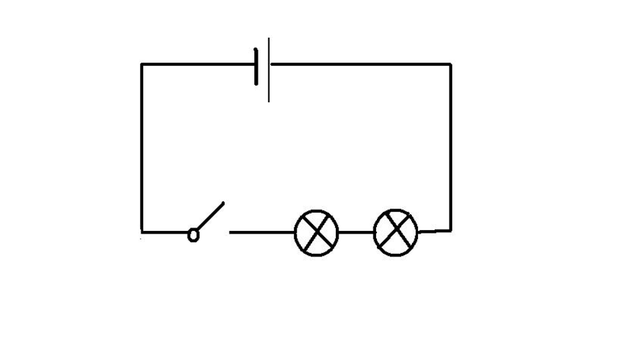
欧姆定律也为解释串联电路中电流处处相等提供了理论基础。

欧姆定律表明，在一段电路中，电流I、电压V和电阻R之间的关系为V=IR。

在串联电路中，总电压等于各个元件上电压之和，即V_total = V1 + V2 + ... + Vn，其中n为元件数量。

同时，由于电流在串联电路中处处相等，我们可以将欧姆定律应用到每一个元件上，得到V1 = IR1, V2 = IR2, 等等。

将这些表达式代入总电压的等式中，我们可以得到V_total = I(R1 + R2 + ... + Rn)。

由此可见，只要电源电压和各元件的电阻值不变，通过每个元件的电流就必然相同。

能量守恒定律同样适用于串联电路的情况。

在一个理想的情况下，电源提供的能量等于电路中各个元件消耗的能量总和。

由于串联电路中的电流一致，根据功率的计算公式P = IV（其中P是功率，I是电流，V是电压），我们可以推断出，电源提供的功率等于各元件功率之和，这也间接证明了串联电路中电流的均匀分布。

串联电路中电流处处相等的现象是由多个因素共同决定的：电流的定义确保了通过每个元件的电荷量的一致性；电荷守恒定律保证了在没有外部电荷注入或流失的情况下，电路中的总电荷量保持恒定；欧姆定律从数学上证明了在给定电压和电阻条件下，电流的唯一性；而能量守恒定律则从能量转换的角度支持了电流均匀分布的观点。

这些原理相互印证，共同构成了串联电路中电流处处相等这一基本特性的理论依据。