作为一个科学爱好者,你可能早已对“分形”这一概念有所耳闻。
简单来说,分形结构就是一种在不同尺度上都呈现相似性的现象。也就是说,当你将一个物体的局部放大时,你会发现它的结构与整体极为相似。
从计算机算法的角度讲,有点像——递归算法,感兴趣的朋友可以自己查一下这个算法。
如果你继续放大这个局部,还是会发现它与之前的形态相似,这种特性可以无限延续下去,这就是所谓的“自相似性”。
在自然界中,许多事物都具有分形的特征,例如海岸线、树枝的分叉以及树叶的脉络等。比如下图一片叶子就有这种奇妙的结构——
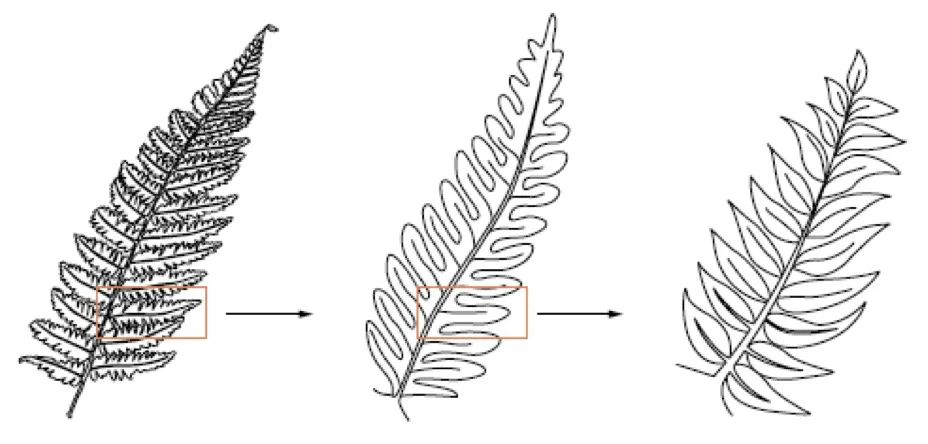
树叶的分形
其实,在我们身处的这个三维世界中,其实很容易理解并观察一维、二维和三维的物体。
甚至刚出生的小孩也有基本观察世界维度的能力。例如,一个盒子有三个维度:长、宽和高。
这三个方向彼此垂直,使得盒子成为一个典型的三维物体。

而一张纸,则只有长和宽这两个维度,我们称之为二维物体。
再进一步,像一根细小的头发,它只具有长度一个维度,因而是一维的。通过这些简单的例子,我们能够轻松理解不同维度的概念。
然而,世界并不总是如此简单明了。
在我们的日常生活中,有一些物体的维度并不符合我们对1维、2维或3维的常规理解。
这些物体的维度不再是简单的整数,而是某种介于整数之间的“分数维”。
一个经典的例子就是科赫曲线,它的维度大约是1.26186,这个数值既不是1,也不是2,而是介于两者之间。
而这种维度就被称为“分数维”。它并不是我们通常理解的那种整数维度,却同样真实存在。
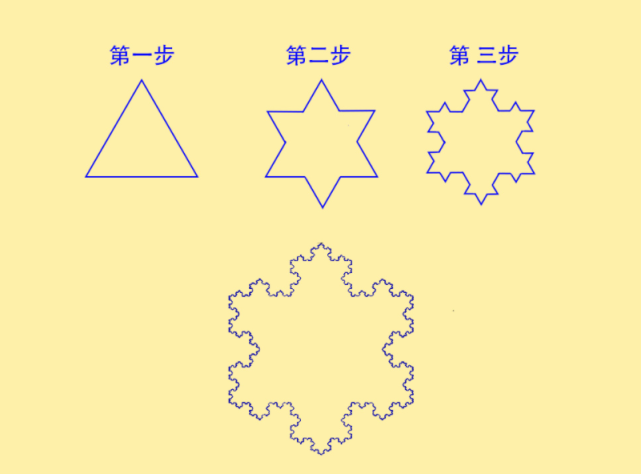
有意思是科赫雪花并非我们通常所见的雪花,而是一种源自数学领域的几何曲线。
它的形状与雪花相似,因此被称为“雪花曲线”。
那么,这个奇特的曲线是如何诞生的呢?
它最早出现在瑞典数学家海里格·冯·科赫的论文中。科赫在他的研究中引入了这一曲线,并展示了它独特的数学性质。
令人惊奇的是,这片看似简单的“雪花”具有无限的周长,理论上甚至可以远远超越地球的直径....,继续看后面你就懂了。

科赫曲线
接下来我们主要来看看这个所谓的分数维究竟是怎么来的或者如何计算的。
01 科赫曲线可视化
理解分数维可能需要一些想象力。
尽管它像盒子、纸张或是马路中央那条线一样真实,但我们无法像观察普通物体那样直观地“看”到它。为了帮助我们更好地理解这一概念,我们可以尝试将科赫曲线可视化。
让我们从一条直线段开始。想象一下,这条线段是一维的,是一根极细的头发。
接下来,我们将这条线段一分为二,并在中间的三分之一处加上一个倒立的“V”字形。
这个“V”字形由两条线段组成,每条线段的长度与被替换的那部分相同。
这样一来,我们的直线段就不再是一条简单的线,而是变成了一种更复杂的形状。
然而,这只是科赫曲线的开始。
接下来,我们要对每次生成的新线段重复这个过程。也就是说,我们不断地对每一条线段进行分割和替换,重复无数次。
即便我们使用计算机模拟这个过程,绘制出的图像也不会是真正的科赫曲线,因为真正的科赫曲线包含了无穷多的细节。尽管如此,这种模拟仍然能够帮助我们直观地感受到科赫曲线的一些特质。
想象一下,如果我们能够沿着科赫曲线行走,这条曲线的长度将是无限的,因为我们不断地沿着一个比直线更复杂的路径前进。
然而,尽管这条路径的长度是无限的,它的宽度却始终有限。我们可以走完这条曲线的全长,但仅仅只走完其宽度的一部分。
这种非凡的曲线让我们重新思考维度的概念。例如,一条线是一维的,因为它只延伸在一个方向上。一个正方形是二维的,因为它延伸在两个方向上。
而一个立方体是三维的,因为它在三个方向上都有延展。然而,当我们面对像科赫曲线这样的分数维物体时,这种传统的理解显得有些不足。
为了更好地理解科赫曲线的维度,我们可以回顾一下传统几何学中的维度定义。
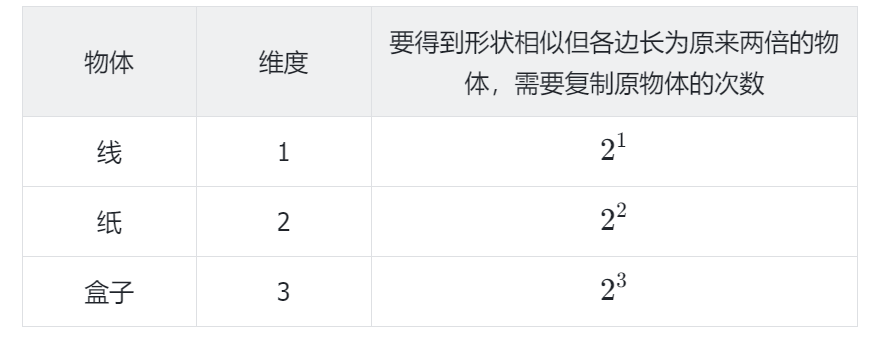
通常,如果我们想将一个n维的物体放大为原来的两倍,我们需要复制多少个原物体?
例如,要将一条一维线段的长度加倍,我们需要2条相同的线段。
要将一个二维正方形的边长加倍,我们需要4个相同的正方形。
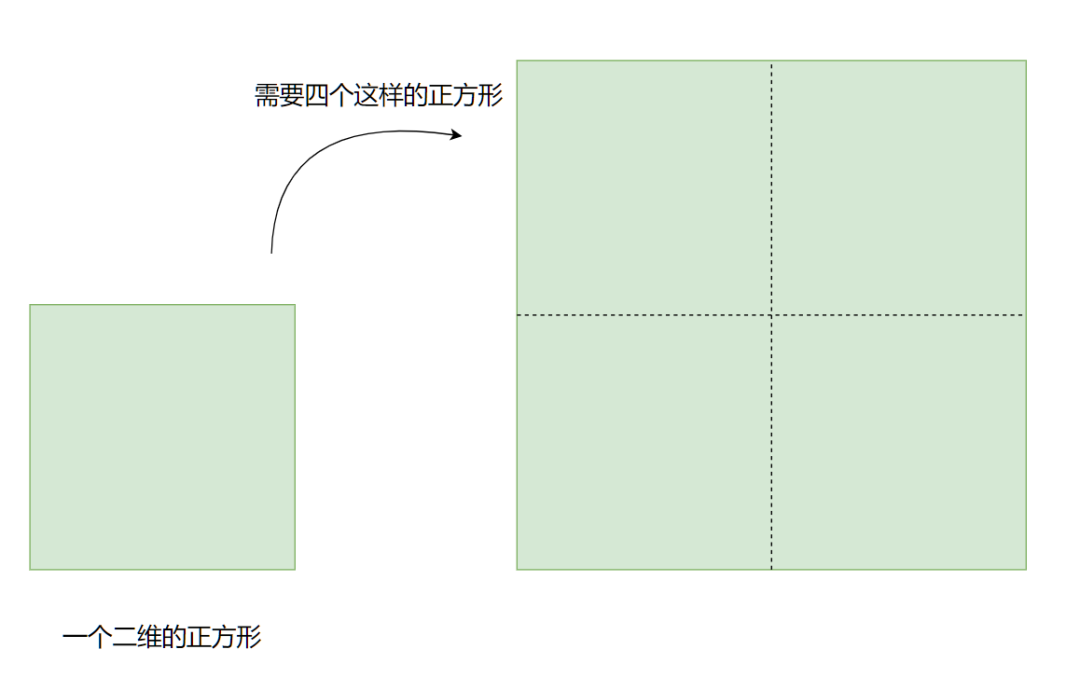
而要将一个三维立方体的边长加倍,我们则需要8个相同的立方体。
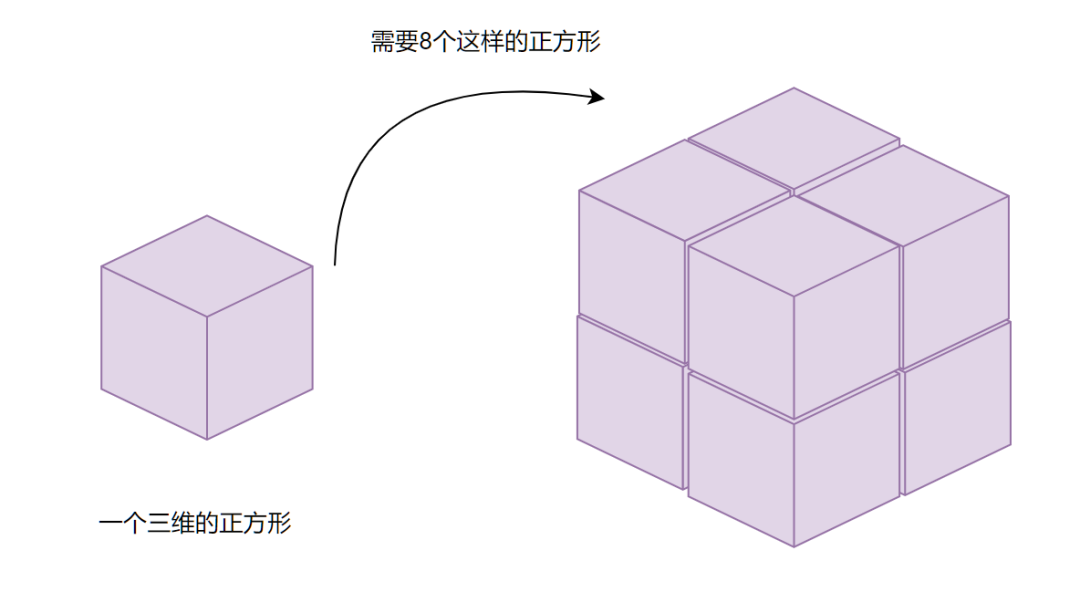
这时,我们会发现,物体的维度正好出现在这个放大倍数的指数上。
也就是说,如果你要将一个n维物体的边长放大为原来的S倍,那么你需要复制S^n个原物体。
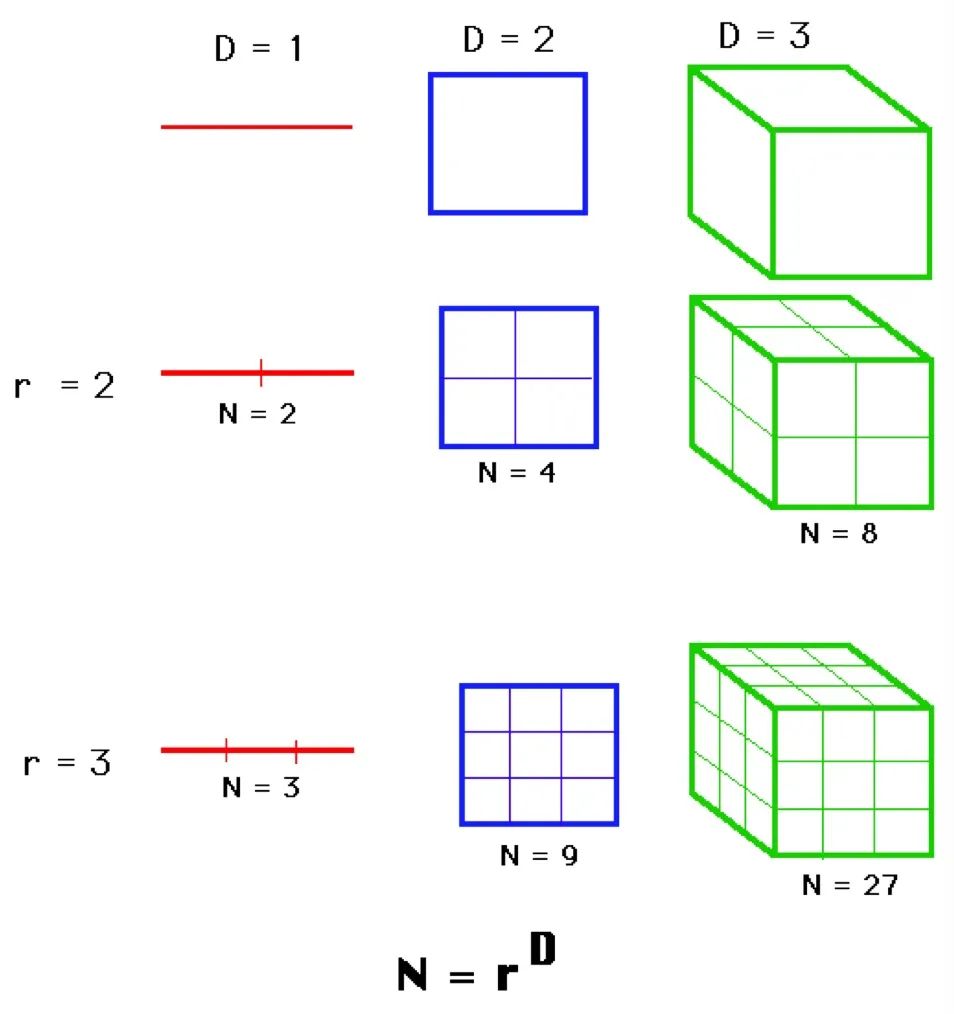
这一维度定义不仅适用于线、纸和立方体这些简单的物体,也同样适用于确定科赫曲线的维度。
那么,科赫曲线的维度到底是多少呢?
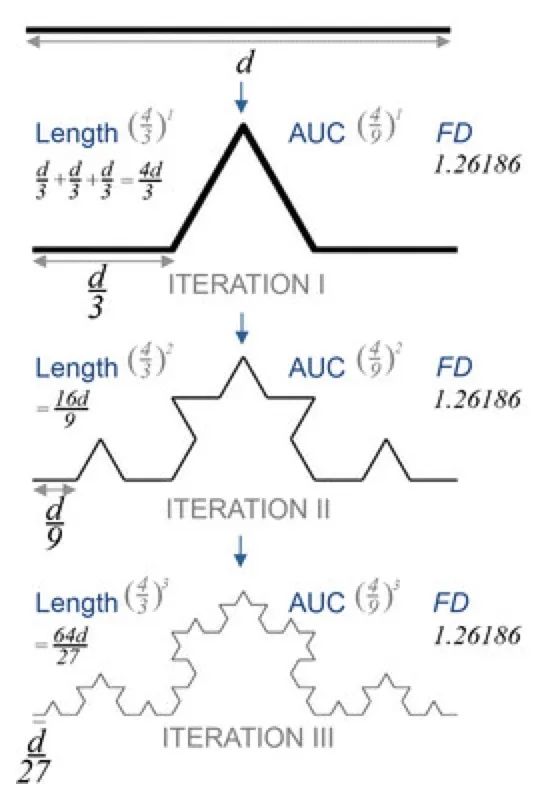
假设我们将科赫曲线放大为原来的三倍。通过前面的构造过程,我们知道需要四个相同的科赫曲线来拼出放大后的曲线。因此,我们可以用以下方程来计算它的维度:
3^d = 4
在这个方程中,d就是科赫曲线的维度。
我们来思考一下这个方程,如果d等于1,那么3^1等于3,而不是4。
因此,d不可能是1。如果d等于2,那么3^2等于9,仍然不是4。所以d也不可能是2。
显然,d必须是一个介于1和2之间的值,这意味着科赫曲线的维度是一个分数。通过计算得出,科赫曲线的维度大约是1.26186,也就是说:
3^{1.26186} ≈ 4
这就首次让我们窥见了一个分数维的世界。在这个世界里,维度不再是我们习以为常的整数,而是介于整数之间的某种“中间状态”。
科赫曲线带给我们的不仅仅是一种数学上的新奇,它还教会我们如何用新的视角看待世界。
当我们发挥想象力去“看”分数维时,我们实际上是在突破传统的思维框架,接受一种不寻常但却可能存在的现实。
这种勇于探索和接受新事物的态度,不仅在数学中适用,在我们的生活中同样重要。
因此,当你下次在生活或学习中遇到选择和困境时,不妨想想科赫曲线。
它告诉我们,即使在看似有限的选择中,也可能蕴含着无限的可能性。只要我们敢于打破常规,勇于探索未知的领域,或许就能发现一个全新的世界。
这是科赫曲线对我们每个人的邀请和启示。