本文根据解析几何距离公式、反比例函数性质和三角形面积基本公式等方法，介绍已知反比例函数xy=3与直线y=x+1的交点为A,B与原点o构成的三角形面积，其面积多种方法计算的主要步骤。

联立反比例函数与直线方程有：

x(x+1)= 3

x^2+x-3=0,

由二次方程的求根公式，有：

x1=-(1+√13)/2，x2=(-1+√13)/2。

则有：x2-x1=√13。

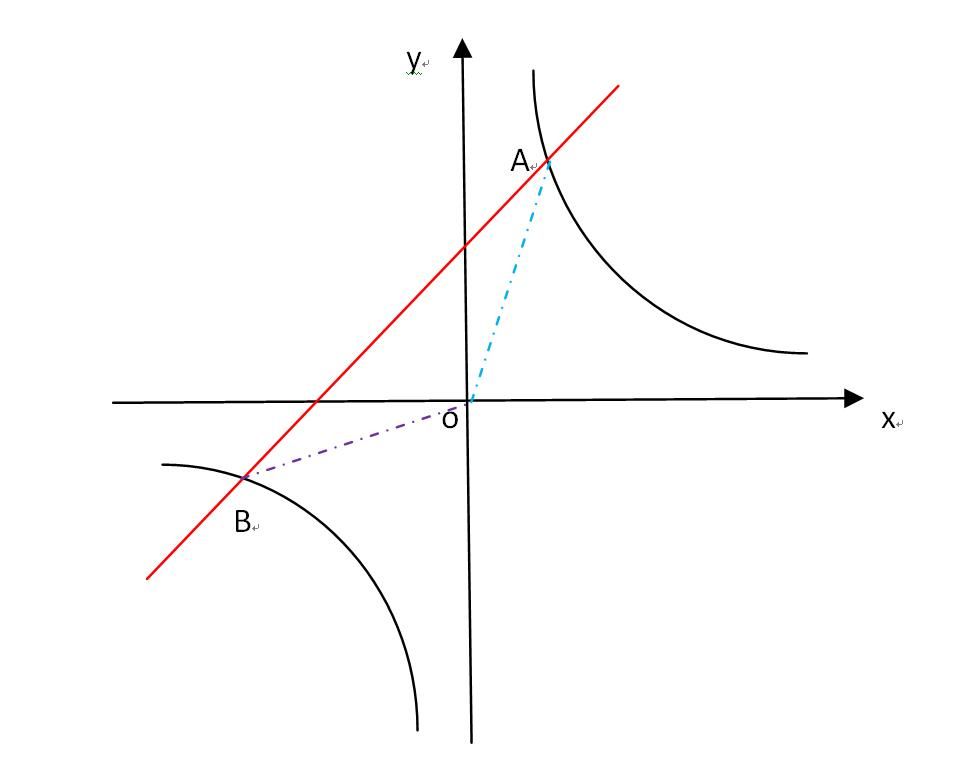
思路：求出函数的交点，根据两点间距离公式和点到直线的距离公式，求解所求三角形的面积。

(1).距离计算

设A(x2,y2),B(x1,y1),由两点间距离同时有：

AB=√[(y2-y1)^2+(x2-x1)^2]

=√[1^2(x2-x1)^2+(x2-x1)^2]

=√(1+1^2)*|x2-x1|

=√(1+1^2)*√13。

原点到直线y=x+1的距离为：

d=|0-0-1|/√(1+1^2)= 1/√(1+1^2)。

(2).面积计算

所以三角形的面积为：

SOAB=(1/2)*AB*d

=(1/2)*[√(1+1^2)*√13]* 1/√(1+1^2)

=(1/2)*√13。

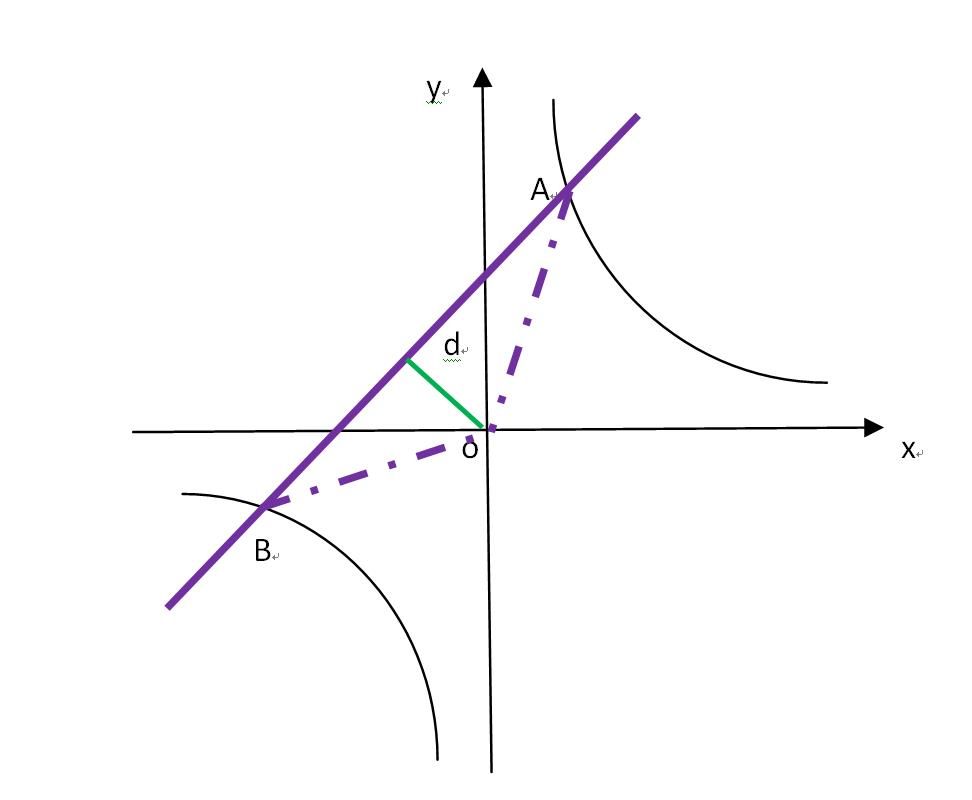
思路：根据反比例函数的几何性质，求解所求三角形的面积。

在反比例函数中，xy=3，其几何意义表示的是三角形OAC的面积，

如下图所示，即：

SOAC=(1/2)*OC*AC

=(1/2)*|x*y|

=3/2平方单位。

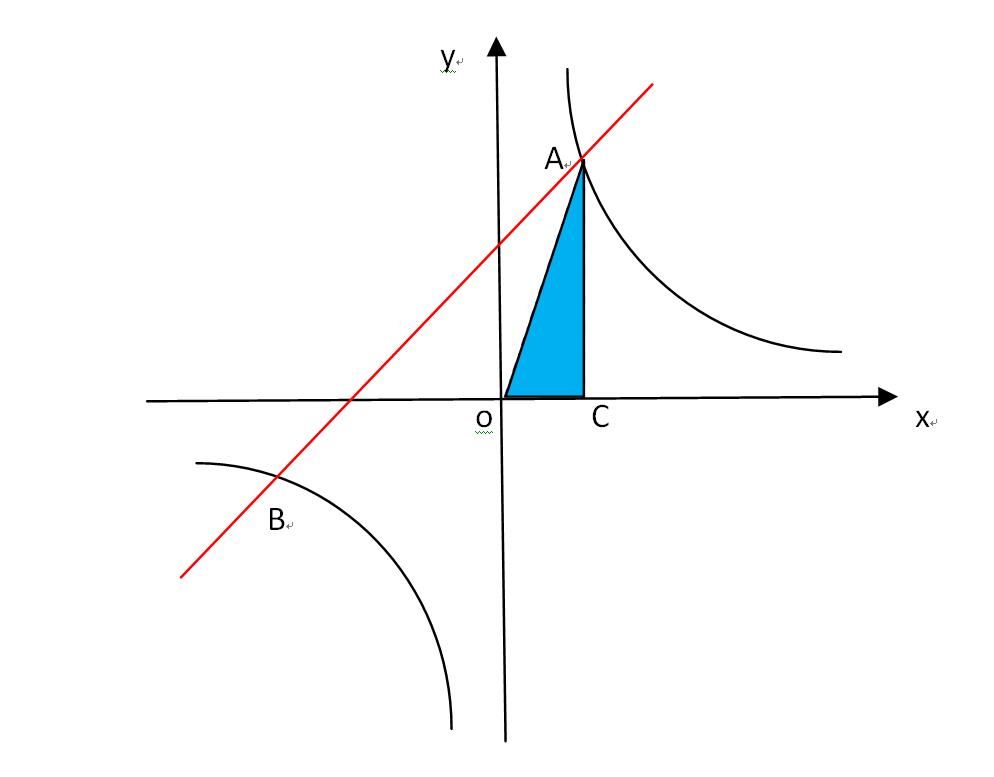
此时所求三角形OAB的面积可以转化为:

SOAB=SABD-SOAC-SOBE-SOCDE

=SABD-3/2-3/2-SOCDE

=SABD-3-SOCDE

=(1/2)*(|x1|+|x2|)(|y1|+|y2|)-3-|x2*y1|

=(1/2)*(x2-x1)(y2-y1)- 3-|x2*3/x1|

=(1/2)*(x2-x1)^2-3-3*|x2/x1|

=(1/2)* (1^2/1^2)*13-3-3*(-1+1√13)/(1+1√13)

=7/2-3*( √13-1)^2/12

=7/2-(7-√13)/2

=(1/2)*√13平方单位。

※.截距式求解：

因为y=1x+1,所以直线与x轴和y轴的交点分别为：

P(-1/1,0),Q(0, 1)，

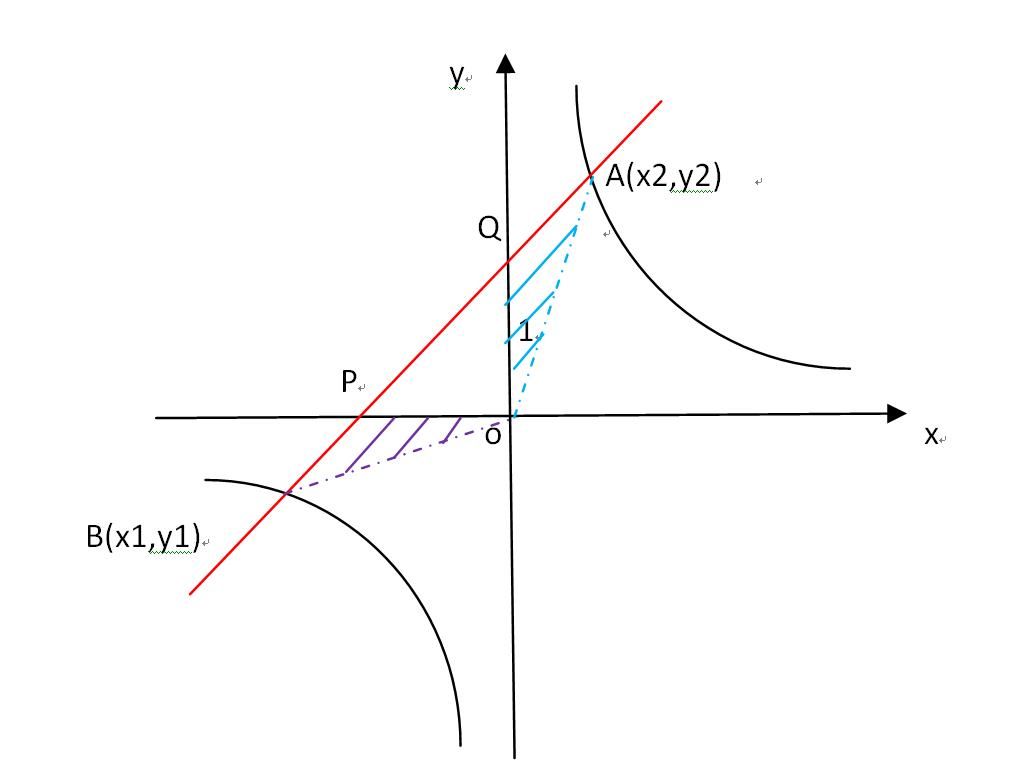
此时三角形AOB的面积为：

SAOB=SAQO+SBPO+SOPQ

=(1/2)*OQ*x2+(1/2)*OP*|y1|+(1/2)*1*|-1/1|

=(1/2)*(1*x2+|-1/1|*|3/x1|)+1/2

=(1/2)*(1*x2+1/1*|3/x1|)+1/2

=(1/2)*1*(-1+1√13)/2+(1/2)*1/1*3/[(1+1√13)/2]

+1/2

=(1/4)*( 1√13-1)+(3/1)*1/(1√13+1)+ 1/2

=(1/4)*( 1√13-1)+(1√13-1)/4+ 1/2

=(1/2)√13平方单位.