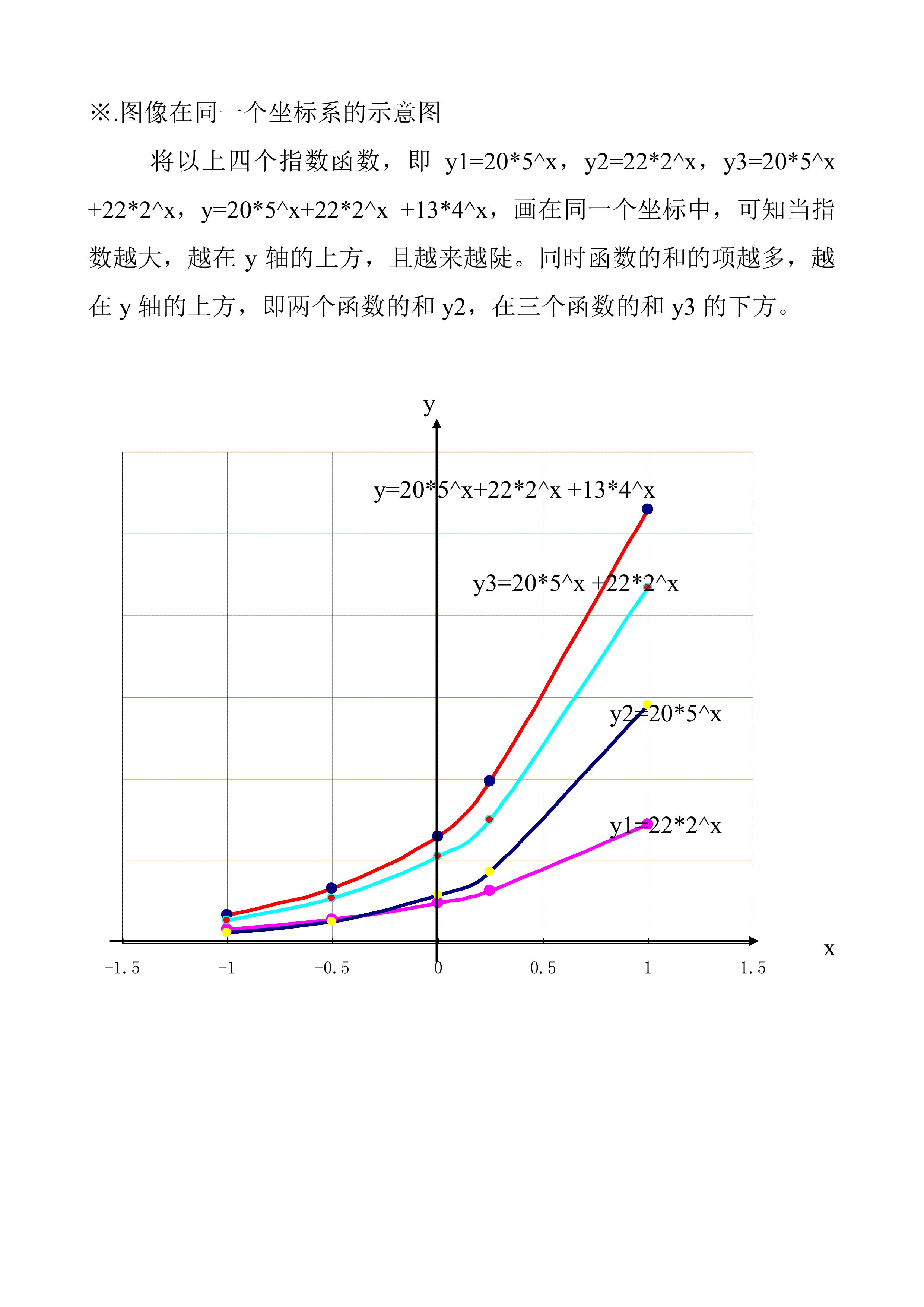
指数函数y=20·5^x+22·2^x+13·4^x的图像变化分析

主要内容：

本文主要介绍单个指数函数及多个指数函数和的性质，以及函数图像示意图。

※.函数y1=20*5^x的图像示意图

此时指数函数y1=20*5^x为单调增函数，函数的主要性质与函数y=5^x的性质基本类似，函数经过点(0, 20)，图像为凹函数，其示意图如下所示：

※.函数y2=22*2^x的图像示意图

此时指数函数y2=22*2^x为单调增函数，函数的主要性质与函数y=2^x的性质基本类似，函数经过点(0,22)，图像为凹函数，其示意图如下所示：

※.函数y3=20*5^x +22*2^x的图像示意图

通过导数判断函数的单调性，有：y=20*5^x +22*2^x，

dy/dx=20*5^x *ln5+22*2^x *ln2>0,所以函数在定义域上为单调增函数，

再次求导，有：d²y/dx²=20*5^x*ln²5+22*2^x*ln²2>0,故函数为凹函数。

※.函数y=20*5^x +22*2^x +13*4^x的图像示意图

同理，通过导数判断函数的单调性，有：y=20*5^x +22*2^x +13*4^x，

dy/dx=20*5^x *ln5+22*2^x *ln2+ 13*4^x *ln4>0,所以函数在定义域上为单调增函数，再次求导，有：d²y/dx²=20*5^x *ln²5+22*2^x *ln²2+13*4^x *ln²4 >0,

故函数也为凹函数，此时示意图如下。