
今天我们说小数学习
“开头这座山”就是【结合图形理解小数的意义】。
01
概况
四年级下册,小数部分是重点。
包括两大块:小数加减和小数乘法。
小数乘法会讲到:一位、两位、三位小数如何相乘、小数结合分数的扩大与缩小、小数乘法规律、小数的四则运算。
这一章节是重点、也是难点。
小数加减这一章节会内容多,但模块少,会讲到:小数的意义、小数比大小、小数加减法。
其中,小数的意义用了三个课时。
这三节磕下来,以后的小数问题就简单了——包括小数乘法部分。

02
如何学习
教科书里说小数的意义是:
(其实书上没有说明确,这是我的总结)
跟分数对应起来,表示几分之几;其实,小数是分数的特殊形式,只是孩子们没学过小数除法,不好讲。
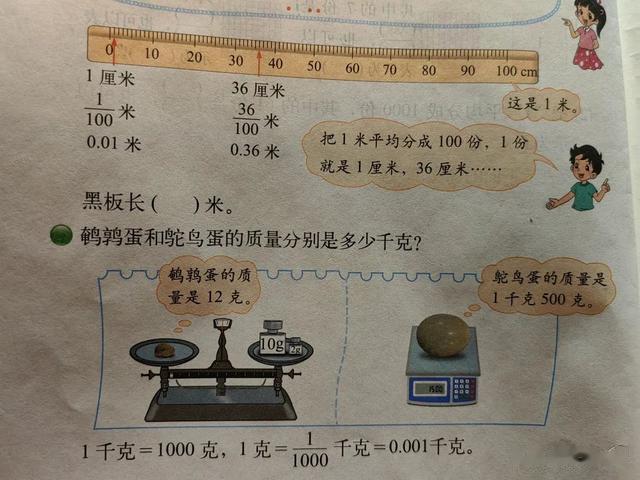
使测量精确又方便;如,测量时不够1米,把这些量分成更小的单位,再来测量,此时引入小数,来表示十分之一米,一百分之一米……。
满足十进制,满十进1。这一点也很关键,跟我们的计数系统对应上了,等于数系扩充了。
之前学了自然数、0、分数,现在加上去小数。
最后会讲小数运算——小数也是符合基本运算律的。
记住,只要数系扩充,就会研究一下这个数是否符合基本运算律。
分数、小数、负数、无理数、虚数……

三个课时,三个意义,层层递进,是后面内容的【底层逻辑】。

学习时,关键要结合图形:
理解小数与分数的对应;明白小数满十进1的特性。(理解这两点,自然知道测量中小数该如何用)
教科书上,使用最频繁的图形是方块图。
一整个方块是一。把方块分成十份,每一份是十分之一,也可以表示为0.1。把方块分成一百份,每一份是一百分之一,也可以表示为0.01。把方块分成一千份,其中的59份,是一千分之59,也可以表示为0.059。……
看起来是不是很简单?
不,不简单,它只是简约。
这样讲就行,说多了,孩子不一定理解。
知识是逐渐加深的——五六年级还会有相关知识,初中还有讲数的。
教科书编得挺好!
(重要提醒:紧扣课本)

学起来时挺好懂的。
因此重点不在理解,而是:把这些图片演示内化到心里。
接下来遇到其他概念都回头想想这里,就能理解透,也能快速学会。
当然,教科书上有练习题。
通过习题,反复地让孩子:
在图上涂一涂,画一画来表示小数。在计数器上播珠子,表示小数。思考用测量模型时,小数如何表示。为的就是:
理解小数和分数的对应;测量中用小数如何表示;通过图形内化小数满十进一的特性。03
示例
用小数表示
当孩子知道一整个方块是1,分成十份,一份是0.1……
他就会:
用小数表示3个方块,两条方块,和两小块方块;也能迁移到钱币、长度单位、重量单位——都是十进制,不同级别的单位相当于方块分了十份、一百份……。因为他心中有对应图:
整个是1;
十分之一是0.1;
百分之一是0.01。

小数加减法
结合图形:
十条是一块,十个0.1是1。
十小块是一条,十个0.01是0.1……
那么:
小数的十分位、百分位、千分位……满十进一的规律也就意会了。
放在小数加减这里,自然的会跟整数加减对应起来。
对于小数加减的计算,在减法的借位和加法的进位上:
学起来很轻松;计算起来不易迷糊。
扩大与缩小
小数乘以整十、整百是扩大十倍、百倍;
一个数乘以0.1,0.01缩小十倍、百倍。
为什么乘反而会缩小?
这对于四年级小学生是反直觉的。
可以回到意义的学习,想想方块图,显而易见:
0.1乘10,也就是十个0.1相加,十个一条是一个整块——放大了。而一个整块,乘以0.1就等于乘以十分之一,那不就是分成10份了吗?分成十份就是缩小了。
继而:
一个数乘以>1的小数是扩大;一个数乘以<1的小数是缩小。孩子也能理解。
<1是把原来的数分成几份,然后取其中的几份,对应到图上是不满1整块了——缩小。
>1是原来的数保留,再加上它的几分之几份,无论后面的满不满一个整体,整个来说就是比原来大——放大了。

PS:
上面这部分书上是利用乘法算式,让孩子找规律。
但你按照上面的方式跟孩子说说,孩子会懂的。
跟接近本质。
小数乘法
小数乘法,你以前是怎么学的?
我们老师教的是:
先把它们当整数乘,得出得数;然后数一数,有几位小数;就把小数点往左挪几位。这种方法好使吗?当然好使!
现在孩子依然可以用。
But,原理是什么?孩子得懂。
还是放大与缩小。

小数变成整数,扩大了、得数也扩大了。
真实的得数,肯定要再缩小回来。
也就是:
把小数当整数乘,
乘完后数一数原来有几位小数,
再从得数上,把小数点往左移几位。
所以,小数乘法是最后一位数位对齐——根本就是整数乘法嘛。
(在列竖式的时候,还要给孩子讲明白如何列,这也是个小知识点)
这扩大与缩小的根儿,不就在图形中嘛!

到这里,说的差不多了。
咱们再总结一下:
小数学习的关键是“结合图形理解小数的意义”。
后面的内容都可以回到意义章节找根儿。
我说完了,你还有要补充的吗?
有的话,欢迎下方留言。
本文结束,谢谢阅读。