尊敬的读者,感谢您在百忙之中阅读我的文章,这是对我努力的肯定,也是持续创作的动力,向您致以我最诚挚的敬意,希望能得到您的一个"关注",在此感谢!
海森堡测不准原理是量子物理学的一个关键要素,它指出不可能同时准确确定物体的位置和速度。物体的位置知道得越准确,其速度的测量就越不准确,反之亦然。这一原理可以比作秋千:一端上升,另一端必然下降。

在数学语言中,不确定性原理表示为位置不确定性(表示为 Δx)和动量不确定性(Δp)的乘积,该乘积始终大于与普朗克常数相关的某个最小值(表示为 ℏ,或简化的普朗克常数)。该常数虽然很小,但在为测量精度提供基本限制方面发挥着重要作用。
这一原理在微观世界中尤其重要,例如对于原子和亚原子粒子。在宏观世界中,由于普朗克常数很小,其影响可以忽略不计。理解这一原理对于理解量子力学很重要,尽管深入理解需要对物理学有深入的了解。
海森堡测不准原理方程如下:
Δx⋅Δp≥ℏ/2
Δx表示位置的不确定性(即确定位置的精确度)。
Δp表示动量的不确定性(即动量确定的准确度)。
ℏ(读作“h-bar”)是约等于 1.0545718×10−341.0545718×10−34 m²kg/s 的约化普朗克常数。
在物理世界中,当涉及低速时,物体的动量定义为其质量乘以速度。这个概念是海森堡方程的基础,该方程演示了速度不确定性与物体位置不确定性之间的关系。然而,人们常常对这个方程的真正含义产生误解,特别是在涉及量子世界的测量时。
这种误解的一个例子是精确确定电子位置的想法。为了检测电子,通常用光“照射”它。光由不同的波长组成,较短的波具有较高的能量。为了准确确定电子的位置,需要波长非常短的光。然而,这就是不确定性原理发挥作用的地方:使用高能光来精确确定电子的位置会为其速度带来更大的不确定性。因此,我们越准确地确定电子的位置,我们对其速度的了解就越不准确,反之亦然,这就是海森堡方程的本质。

量子物理学的基本方面之一是观察微观物体时光的波长所施加的限制。不可能看到小于所用光波长的物体。在观察电子等粒子时尤其如此。
经典的解释是,使用非常短的波长、高能光来观察电子会导致光子与电子碰撞,从而改变其速度。这种相互作用造成碰撞后电子速度的不确定性,这似乎是对海森堡不确定性原理的明确解释。然而,这种方法更可能指的是观察者效应,即测量行为影响测量对象,而不是海森堡原理的本质。
事实上,海森堡的不确定性原理更深入,与电子和光子等物质的波动性有着千丝万缕的联系。这一原理超越了观察者和物体的简单相互作用,反映了波函数的基本属性和量子世界不可或缺的不确定性。

要理解量子世界,重要的是要认识到亚原子粒子的位置是通过波函数确定的。该函数是指示粒子的可能位置的概率分布。在波函数振幅较大的区域中,找到粒子的概率较高,反之亦然,在波函数振幅较小的区域中,找到粒子的概率较低。
量子力学的一个关键方面也是波粒二元论,它指出亚原子粒子同时具有波和粒子的性质。当被视为波时,这些粒子具有与其动量密切相关的特定波长。因此,具有高动量的粒子具有短波的特征,而具有较低动量的粒子具有长波的特征。这两个关键原理——波函数和波粒二象性——是量子物理学中许多现象的基础,有助于解释为什么亚原子粒子的世界与我们日常的宏观经验如此不同。
在海森堡测不准原理的背景下,当亚原子粒子的动量已知时,粒子的确切位置仍然不确定。在这种情况下,描述粒子的波函数是在两个方向上传播的无限拉伸的波。但是,如果您想了解粒子的位置和动量,则需要修改波函数。
这是通过对波长略有不同的不同波函数求和来实现的。从一个波开始,逐渐添加其他波,每个波都有自己独特的波长。结果,累积波函数(所有这些波的总和)逐渐从简单的正弦波转变为更局部的形式。这个过程演示了许多具有不同波长的相似波的组合如何导致波函数形状的显着变化。
这种技术称为傅里叶变换,是量子物理学中的关键数学工具。它允许波函数分解为其分量波,从而深入了解量子世界中位置和动量之间的关系。
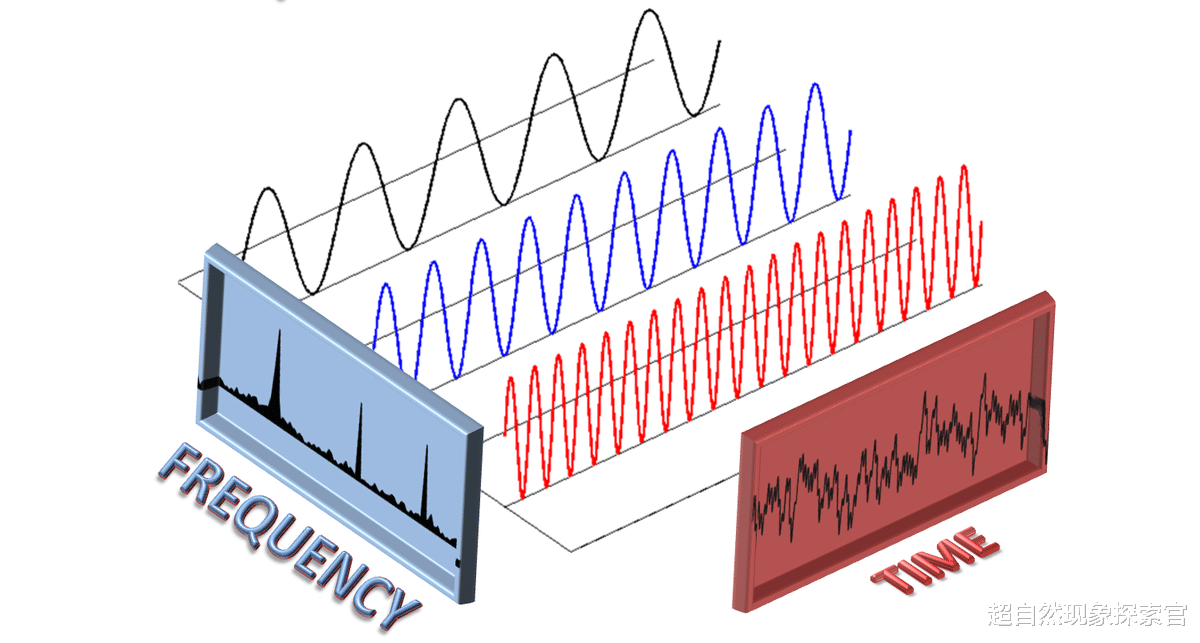
有趣的是,任何波函数形状都可以通过组合许多具有不同波长和幅度的波来合成。从单波长的简单示例开始,这一说法在实践中得到了证明。
当仅考虑一种波长时,位置图显示标准正弦波。然而,当额外的波长被引入到该过程中时,每个波长具有相同的幅度,结果是一个更复杂和局部的波函数。进一步添加各种波长会产生更明确的波函数。该过程的高潮是每个波长以相等的幅度混合,从而产生完全局域化的波函数。
这个概念与海森堡的测不准原理直接相关。如果只有一个波长与粒子的动量或速度相关,那么有关该粒子位置的信息就变得不确定——波函数会到处传播。海森堡不确定性原理的本质是,对一个方面(例如动量)的清晰理解会导致另一个方面(例如位置)的不确定性。
理解这一原理的关键是,粒子的位置确定得越精确,所需的波长范围就越宽。另一方面,波长范围限制得越多,有关粒子位置的可用信息就越少。
此外,海森堡不确定性原理还有另一种表述,将能量 (E) 和时间 (t) 的不确定性联系起来。根据这个公式,能量和时间的不确定性的乘积总是超过简化的普朗克常数的一半,这个版本的原理在研究亚原子粒子的质量和寿命时特别有用。
对于寿命较长的粒子(表示为较大的 Delta t),其能量(或质量)的不确定性很小。这意味着这种长寿粒子的质量实际上是恒定的。

相比之下,仅存在很短时间(小 Delta t)的粒子的特点是能量或质量具有显着的不确定性。这些寿命较短的粒子在平均值附近的质量范围很广,从而导致其物理特性发生变化。
这种根本差异解释了为什么亚原子粒子(例如顶夸克或 W 和 Z 玻色子)可以具有不同的质量。同时,更稳定的粒子,例如电子,具有几乎相同的固定质量。
因此,海森堡的测不准原理提供了深刻的见解,解释了为什么不可能同时精确地知道亚原子粒子的位置和速度,以及它的能量和寿命。充分理解这一原理的各个方面和含义需要时间,但对其关键概念的基本理解代表了量子物理学研究的重要一步。
评论列表