这是那些乍一看很复杂但却出奇地容易解决的问题之一。

我能做到这一点的唯一方法是对等式的两边进行变换，直到我可以进行一些比较并找到m的值。

如果您有其他方法可以解决此问题，我很乐意在评论中看到。

挑战是在m为自然数的条件下找到m的值。

拿起笔和纸，试一试。让我在评论中看看你猜对了什么！如果你答对了，就击掌庆祝吧！但如果答错，也不要着急——跟着做就行了。

如果这个挑战引起了你的兴趣，请查看下面的其他谜题列表！

你准备好了吗？让我们开始吧！

我希望我们采取的第一步是将m放在等式的一边，将数值放在另一边。

为了实现这一点，我们将两个实体都提升到 1/m 次方。

这给了我们：

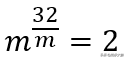
我们接下来要做的就是将两个幂乘以1/32。

美丽的！

现在，表达式左边有未知数m ，而右边有数值。

从这里开始，我们做一件事。

让我们将两个实体的权力乘以8/8。这不会改变权力的值。

目的是将右侧的值转换为左侧的形式。

为什么是8/8？

之前，我在纸上解决这个问题时，尝试过将幂乘以2/2。我连续尝试了两次都没有成功，但第三次尝试时终于成功了。

重复做这些事情会让这篇文章变得冗长。因为2/2 * 2/2 * 2/2等于8/8，所以我们继续使用8/8。

在左侧这样做确实毫无意义。我们可以消除它，将更多精力放在右侧。

这给了我们以下信息：

你注意到了什么？

现在右侧的值与左侧的值的形式相同了。太棒了！

现在我们可以进行比较了。m 的值为 256！