前面我们提到在《西方哲学》中,毕达哥拉斯是一个非常重要和神奇的人物,不仅仅是因为他说了一句“人不可能同时踏进同一条河流”,还因为他在数学和哲学中有着神奇的发现,今天第一集就是他发现的耳熟能详的的定理:勾股定理——勾股定理是我们上学时候的必修几何课,一个正方形的对角线的平方等于两边平方之和。当然这个定理的发现比我们西周的商高发现勾三股四弦五还是晚了500年。

据说当时在一个古老的希腊小村庄,在那里有一位叫做劳拉的农夫。劳拉是一个好奇心旺盛的人,他喜欢用自己的智慧解决各种难题。然而,他却一直感到困惑——如何准确测量不规则的土地面积,尤其是直角三角形的面积呢?有一次劳拉偶然听说了有一位智者毕达哥拉斯,是数学的教父,可以回答一切数学问题。劳拉抱着忐忑的心情,决定亲自去拜见这位传说中的大师。
终于,劳拉来到了毕达哥拉斯的学院,见到了这位令人肃然起敬的数学家。毕达哥拉斯对劳拉的问题一下子就有了答案,他告诉劳拉,只需要在一个直角三角形的两条直角边上,分别取长度为3和4的线段,然后将这两条线段延长成为等长的线段,再与原来的两条直角边连接,就会得到一个完整的正方形。而两个小的正方形面积之和等于大的正方形面积,从而得出了勾股定理。
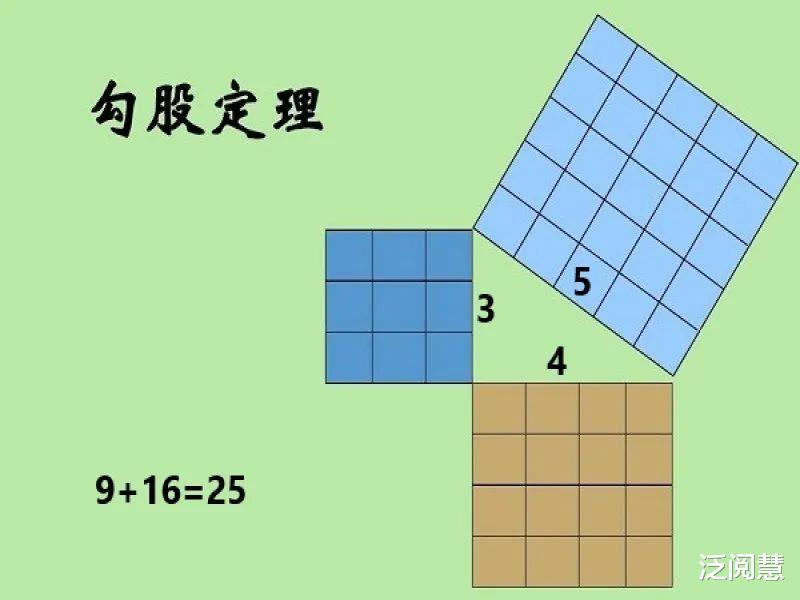
劳拉听得着迷,迫不及待地去试验了毕达哥拉斯的想法。他将线段以及直角边连接在一起,最终确实得到了一个完美的正方形。劳拉欣喜若狂,他意识到这个正方形的面积和原来的直角三角形一模一样!这就是著名的勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。
这个发现极大地促进了劳拉的工作,他开始利用勾股定理,准确测量不规则土地的面积。他的农田愈发养眼,惹来了许多人的围观和赞叹。而毕达哥拉斯的智慧也传遍了整个希腊。

毕达哥拉斯成为当时最受崇拜的数学家之一,人们纷纷前来向他请教数学难题。他用简单的几何图形和勾股定理解决了无数难题,让人们眼界大开,对数学产生了浓厚的兴趣。勾股定理也不再局限于解决土地测量问题。它在建筑、天文学、航海、工程等领域都发挥着重要作用。人们开始意识到数学的力量和智慧,勾股定理成为数学发展史上不可或缺的重要一环。
如今,勾股定理已经成为数学课本中的经典,所有学生都会在学习数学的过程中遇到它。不只是数学家,即使是普通人也会被这个有趣的定理所吸引。勾股定理不仅拥有科学的内涵,更是对人类思维力的一次极佳锻炼。