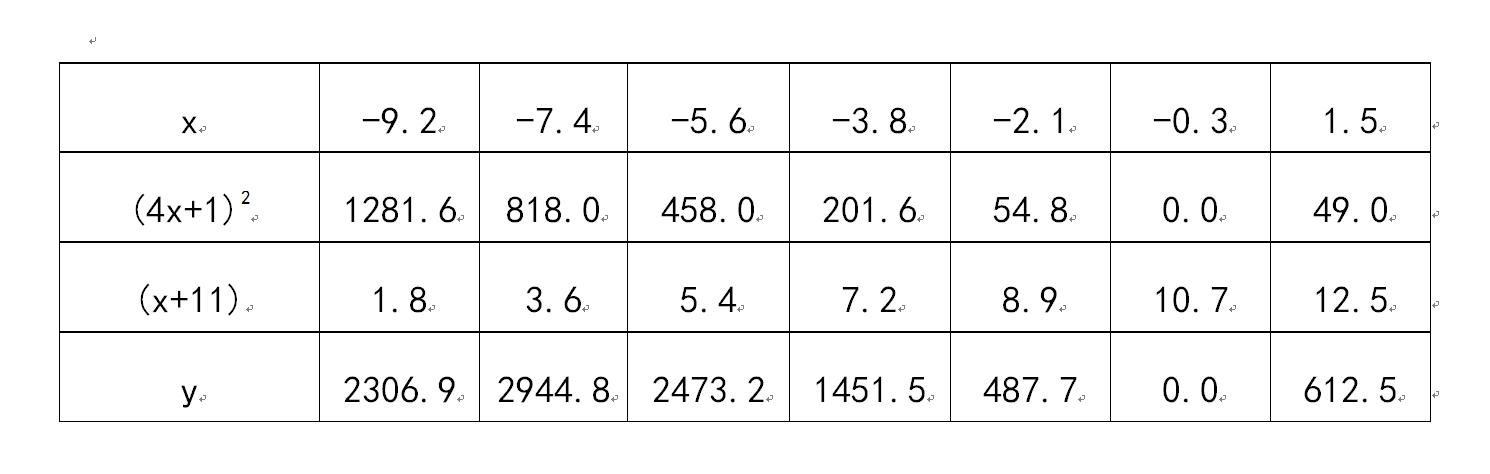
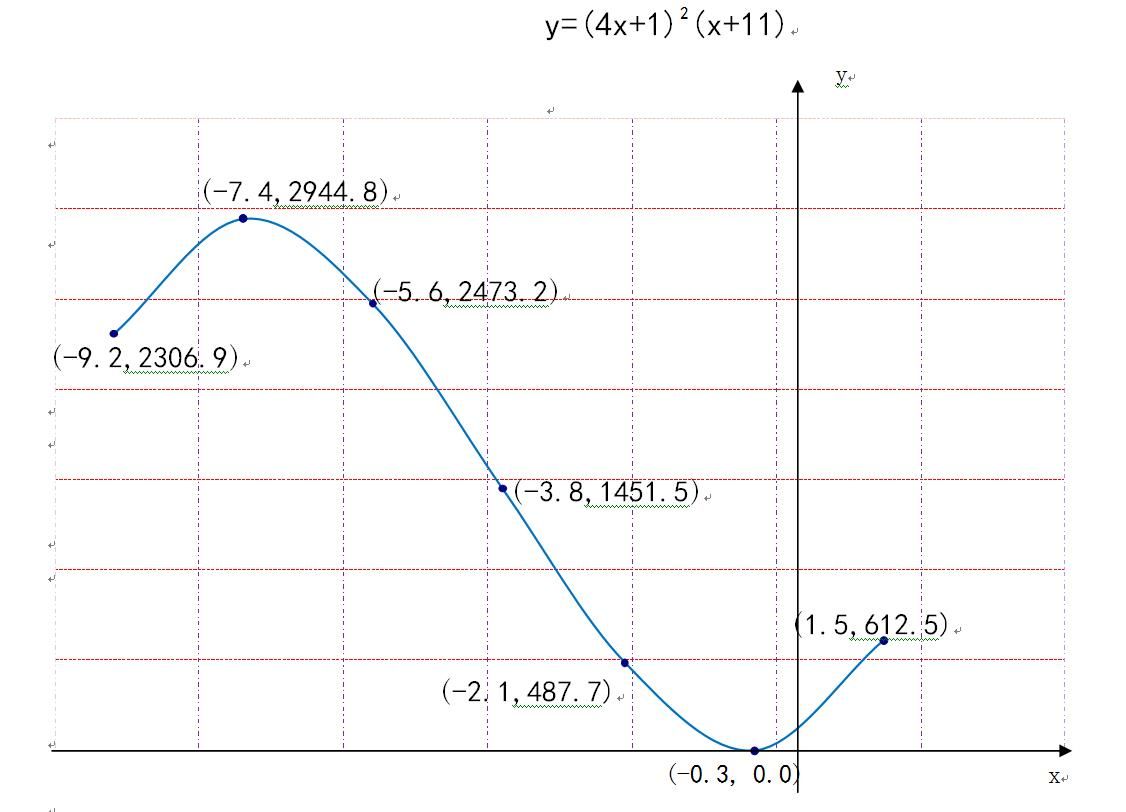
通过函数的定义域、值域、单调性、凸凹性及极限的性质，并通过函数导数知识求解函数的单调区间和凸凹区间，并简要画出函数y=(4x+1)^2(x+11)示意图的过程与步骤。

根据函y=(4x+1)^2(x+11)特征，可知函数自变量x可以取全体实数，即函数的定义域为：（-∞，+∞）。

本处通过导数工具来解析函数的单调性，过程如下：

∵y=(4x+1)^2(x+11)，

∴y'=8(4x+1)(x+11)+(4x+1)^2，

=(4x+1)[8(x+11)+(4x+1)]

=(4x+1)(12x+89)

令y'=0，有4x+1=0，12x+89=0，即：

x1=-4/4≈-0.3，x2=-89/12≈-7.4.

(1).当x∈(-∞，-7.4)，(-0.3,+∞)时，

dy/dx>0,此时函数为增函数。

(2).当x∈[-7.4，-0.3]时，

dy/dx<0,此时函数为减函数。

∵y'=(4x+1)(12x+89)

∴y''=4(12x+89)+12(4x+1)

=16(6x+23).

令y''=0，则6x+23=0，即：

x=-23/6≈-3.8.

此时函数的凸凹性性及凸凹区间为：

(1)当x∈(-∞, -3.8)时，y''<0,此时函数y为凸函数。

(2)当x∈[-3.8,+∞) 时，y''>0,此时函数y为凹函数。