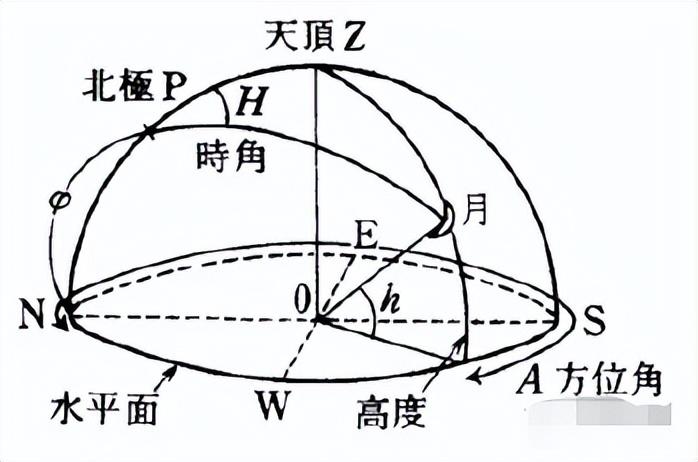
在测绘工作中，方位角是最基本的方位元素，也是导航定位和航空飞行等领域的重要元素。所谓方位角，是指从北开始的顺时针旋转角度，指示了目标相对于真北的方位。

具体来说，我们可以将方位角分为真方位角和磁方位角两种。真方位角以地球的真北方向为基准，而磁方位角则是以地球的磁北极方向为基准。在实际测量中，我们通常使用磁罗盘测量得到的磁方位角。

方位角的计算方法有多种，最常用的是迭代法和正算法。迭代法通过多次计算得到目标相对于真北的角度，而正算法则是直接计算出目标相对于真北的方向。下面我们就来介绍一下计算方法。

1. 根据坐标值计算方位角：

使用以下公式可以根据两个坐标值计算方位角：

其中，AA为起点到终点的方位角，\text{起点}起点和\text{终点}终点为相应坐标的数值。请注意，AA的值可能会受到所使用的坐标系的影响。

2.迭代法

迭代法是一种比较常用的计算方位角的方法，它的基本思想是将目标点的坐标和起点的坐标代入以下公式：

tan θ = (y2 - y1) / (x2 - x1)

其中，θ表示角度，y2和y1分别表示目标点和起点的纬度，x2和x1则表示目标点和起点的经度。通过多次迭代计算，即可得到目标点相对于起点的方位角。

3.正算法

正算法是一种直接计算目标点相对于真北方向的计算方法，它主要借助了三角函数的知识。假设目标点和起点的坐标均已知，我们可以使用以下公式进行计算：

cos A = sinφ2 - sinφ1 * cos(λ2 - λ1) / cosφ1 * sin(λ2 - λ1)

其中，A表示目标点相对于真北的方位角，φ1和φ2分别表示起点和目标点的纬度，λ1和λ2则表示起点和目标点的经度。

需要注意的是，在实际测量中，还需要考虑磁偏角和地球自转等因素的影响，这些影响会对方位角的计算产生一定的影响。因此，我们在计算方位角时需要特别谨慎。