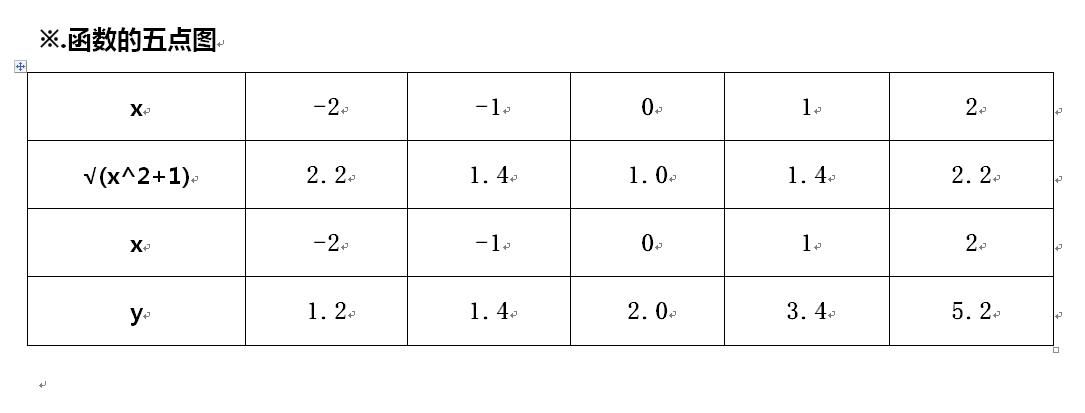
本文主要介绍函数y=√(x^2+1)+x+1的定义域、单调性、凸凹性,并简要画出函数的图像示意图。
※.函数的定义域∵x^2+1>0,
∴函数的自变量x可以取全体实数,
即函数的定义域为:(-∞,+∞)。

对于函数y1=√(x^2+1)在定义域上为增函数,函数y2=x+1在定义域上为增函数,所以其和函数y=y1+y2在定义域上也为增函数。
同时,本题还可以通过导数知识判断函数的单调性,过程如下:
∵y=√(x^2+1)+x+1
∴y'=2*x/2√(x^2+1)+1
=x/√(x^2+1)+1>0,
即函数在定义上为单调增函数。
※.函数的凸凹性∵y'=1+x/√(x^2+1),
∴y''=1*[√(x^2+1)-x^2/√(x^2+1)]/(x^2+1),
=1*[(x^2+1)-x^2]/[√(x^2+1)*(x^2+1)],
=1/√(x^2+1)^3>0,
则函数y在定义域上为凹函数。

lim(x→-∞)√(x^2+1)+x+1=-∞,
lim(x→0)√(x^2+1)+x+1=2,
lim(x→+∞)√(x^2+1)+x+1=+∞,