今天我们来说遇到中点如何作辅助线

01

构造中位线

第一种：直接连起来

当你看到题目中有有两个、两个以上的中点，首先考虑的就是：

把这两个中点连接起来，这样就得到了一条中位线。

在三角形中：

中位线平行于底边；是底边的1/2。

这样在求线段长度的问题上能帮我们破局。

看下面这一题。

说D和E是两个中点，我们首先想到把它俩连接起来。

得到中线DE。

DE是平行且等于1/2BC的，它的长度知道后，我们就可以利用勾股定理算出EF的长。

再看下面这个。

图中D和E是两个中点，我们把它连接起来，得到DE 。

DE平行于AB，那么我们根据平行就得到一对蝴蝶型的相似三角形。

这两个相似三角形的相似比是1比2，那么我们就可以根据这个关系来算出DF的长。

DF的长出来了，那么AD的长也出来了，我们就可以算三角形的面积了。

第二种，做平行线得到中位线

题目中没有两个中点——只有一个，甚至一个也没有，比较隐晦，你需要自己找到。

找到之后，从这个中点往对边做一条平行线，这样你就得到了一条中位线。

接下来咱们就可以利用中位线的性质来做一些求解。

看下面这道题：

D是AC的中点，我们就从D作一条平行于BC的线段DF，这条线段就是中线。

那么F也是AB的中点，然后再根据中线平行于底边,得到一对蝴蝶型全等的三角形。

边的关系，我们就可以算出来了。

这就是构造中位线的两种方法：

一种是有明显的中点，你就直接连接；一种是有一个中点，或没有说中点的事，你找到中点后大胆作平行线就构造了中位线。

有中位线后，利用中位线的的性质，可以很巧妙地解决一些问题。

02

构造中线

中线和中位线不一样。

中线是三角形的一个顶点到对边中点的连线。

通常在等腰三角形中，中线和垂直平分线、角平分线三线合一。

所以，遇到等腰三角形，我们作中线，会得到：

角相等、线段相等、垂直——

利用这些特殊性质，做题很流畅。

构造中线的两种方法。

第一种，已知等腰三角形，作它底边上的中线。

比如下面这两道题。

第8题是作了中线后，找到了等量关系，求解出我们需要的长度。

第9题是根据中线的性质，找到了全等关系，然后得出了我们需要的关键线段的长度。

第二种，在直角三角形中构造中线。

我们都知道直角三角形斜边上的中线等于斜边的一半。

当你遇到一个直角三角形，就作它斜边上的中线。

如此一来，我们可以利用中线和斜边被分开的两条线段相等，得到很多相等关系。

比如下面这3道题。

第10题。

三角形ABC是直角，D是AB边上的中点。

连接CD——构造中线。

那么CD就等于斜边的一半，也等于4，这样我们可以得到一个等腰三角形DCB。

又因为角度关系，我们可以得出EC＝CD。

第11题。

还是构造中线，连接CE。

我们得到等边三角形ACE，从而可以算出BC的长度。

BC的长度有了CD也能算出来。

然后我们就可以在直角三角形CDE中，利用勾股定理来算DE的长度了.

第12题

第12题稍微复杂一点，我把解题过程写一下。

这就是构造中线的两种方法，主要集中在特殊三角形中。

情况一旦特殊，其实还好办了。

关键是不特殊。

如果不特殊怎么办呢？不特殊就想办法让它特殊。

下面说第三种方法。

03

构造倍长中线

是这样的：

我们把中线延长至原来的两倍长。

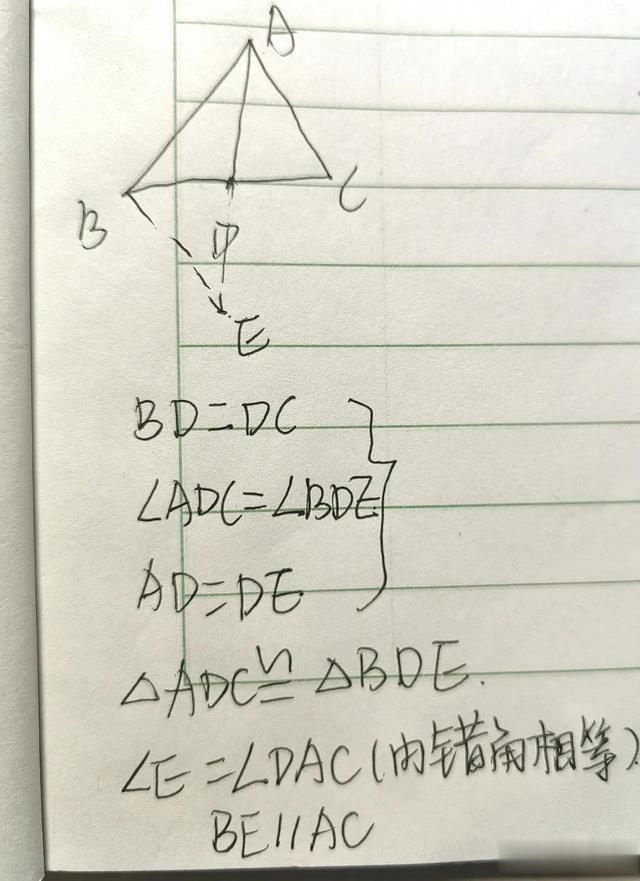
比如在三角形ABC中AD是中线，那么我们延长AD到E点，使DE=AD，那么AE就是二倍的AD。

这样可以得到一对全等的三角形，也得到了一对平行关系。

有了全等和平行，这不就特殊了吗？！

在这些特殊关系的加持下，计算角度、长度，都简便许多。

看下面这道题。

当我们作出倍长中线AE，得到全等三角形。

那么，BE的长度我们就知道了＝6。

而通过角度计算，三角形BCE是个等腰三角形，那么BC的长度我们就知道了。

上面是一个简单的填空题，下面我们再看一个大题。

这道题也不难，但它是倍长中线的一个探索过程，对我们会很有启发。

在这道题中:

第一问，带我们探索了倍长中线构成的全等三角形；第二问，探索了倍长中线的长度范围，放到三角形中，也不难理解。第三问，拓展延伸，这里利用了两次全等。

第一次全等是倍长中线构成的全等三角形。

第二次是由全等三角形得出的线段相等和角度相等，进一步得出一对全等三角形。

好，到这里我们就总结完了。

回顾一下，遇到中点：

我们可以构造中位线、中线、倍长中线，利用“特殊性”解决问题。

你发现没，做辅助线，看起来难，其实无非是根据题意，看看题目上有什么，你往前多想想。

一次想不对，就多试试，试几次就有谱了。自己想不出来，就看看别人的，学过来，总结一下，下次就行了。

只要你带着脑袋学习，哪怕这颗脑袋运行得慢一些，也没多大关系。

有心就行。

谢谢阅读，本文结束。