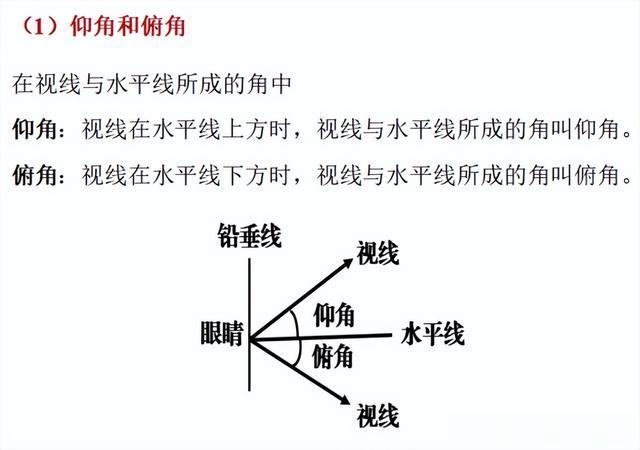
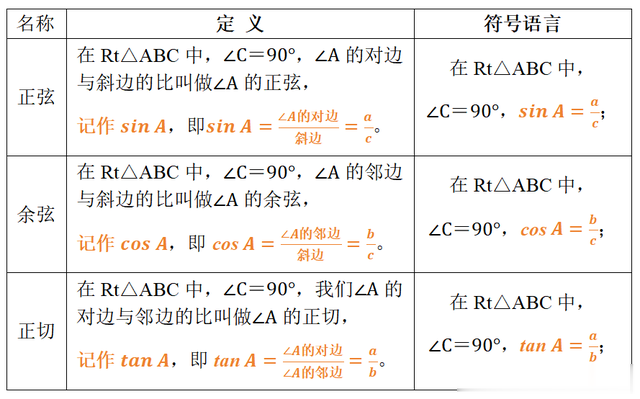
01（一）正弦、余弦、正切

说明

使用范围：正弦、余弦、正切都是在直角三角形中定义的，反映了直角三角形边与角的关系。

三角函数本质：正弦、余弦、正切都是一个比值，是两条线段长度的比，是没有单位的数值，它们只与锐角的大小有关，而与三角形的大小无关。

三角函数思想：∠A的正弦、余弦、正切都是∠A的锐角三角函数。sinA、cosA、tanA都是以锐角A为自变量的函数，一旦A的度数确定，它们的值就唯一确定，即锐角三角函数值随角度的变化而变化。

三角函数的取值范围：由于直角三角形的斜边大于直角边，且各边的边长均为正数，所以锐角三角函数值都是正实数，且0<sinA<1，0<cosA<1，tanA>0。

02书写方式

0330°，45°，60°角的三角函数值

04锐角三角函数之间的关系(拓展)

05解直角三角形

说明

在直角三角形中，除直角外的五个元素中，已知其中的两个元素（至少有一个是边），就可以求出余下的三个未知元素。

06几个常见角度的锐角函数值

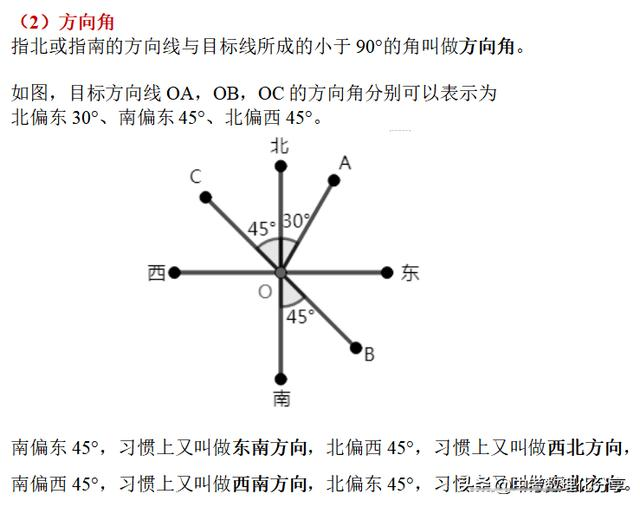
07锐角三角函数的应用

类型一

说明

在图上构造直角三角形，最常用的方法是作“高”，构造一个或两个直角三角形，再利用三角函数和勾股定理解题。

类型二

类型三