大家好！本文和大家分享一道2019年江苏高考数学真题。这是2019年江苏高考数学试卷的第12题，本题考查的是平面向量的数量积，但是很多同学却不会做，下面老师和大家分享两个常用的解法。

解法一：基底法

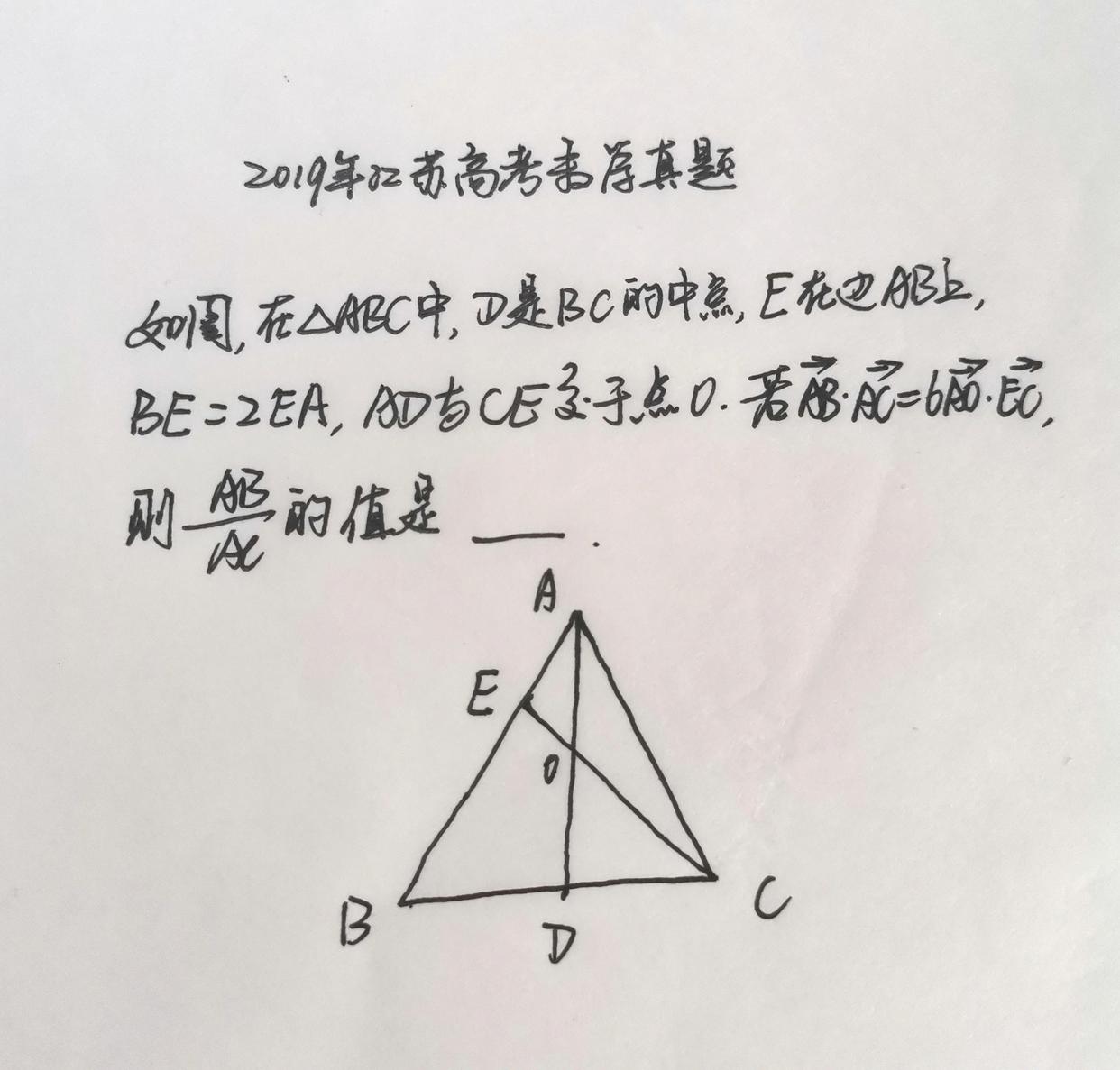
用基底法求向量的数量积，那么首先要选择一组基底，本题中可以选择AB向量和AC向量作为基底，那么接下来就需要用这组基底分别表示出AO向量和EC向量。

本题的难点就是用AB向量和AC向量来表示AO向量。仔细观察图形，我们可以猜测AD=2AO，那么怎么能够得到这个关系呢？过点D作DF//AB交AB于点F。由于BE=2EA，点D为BC的中点，所以可以得到BF=FE=EA，从而得到点O是AD的中点。

于是，AO向量的2倍就等于AD向量，而AD向量等于AB向量与AC向量的和的一半。

接着来表示EC向量。EC向量等于AC向量减去AE向量，而BE=2EA，则AE向量等于三分之一AB向量，代入后就可以表示出EC向量。

然后求出AO向量与EC向量的数量积，再根据题干中的等量关系，就可以求出AB/AC的值。

解法一的难点是用AB向量和AC向量来表示AO向量，那么有没有其他方法呢？当然有，对于一些比较难的平面向量的题目，我们通常可以用坐标法来处理。

以点D为坐标原点，以BC所在直线为x轴，以BC的垂直平分线为y轴，建立平面直角坐标系xOy。由于点D是BC的中点，所以不妨设B(-a,0)、C(a,0)、A(b,c)。从图可知，a＞0、b＞0。

由于BE=2EA，则可以根据定比分点或者向量表示出点E的坐标为((2b-a)/3,2c/3)。现在就只差点O的坐标了，而点O是直线AD与直线CE的交点，所以需要先求出这两条直线的方程，再联立即可求出点O的坐标为(b/2,c/2)。

接下来，表示出向量AB、向量AC、向量AO和向量EC的坐标形式，再根据向量数量积的坐标形式就可以得到一个关于a、b、c的关系。即a^2+b^2=-c^2+4ab①。

知道了点A、B、C的坐标，根据两点间距离公式就可以分别求出AB、AC的表达式，再将①代入就可以得到答案了。

本文分享了两种解法，其实本题还可以利用三点共线来求解，有兴趣的同学可以下去自己尝试一下。