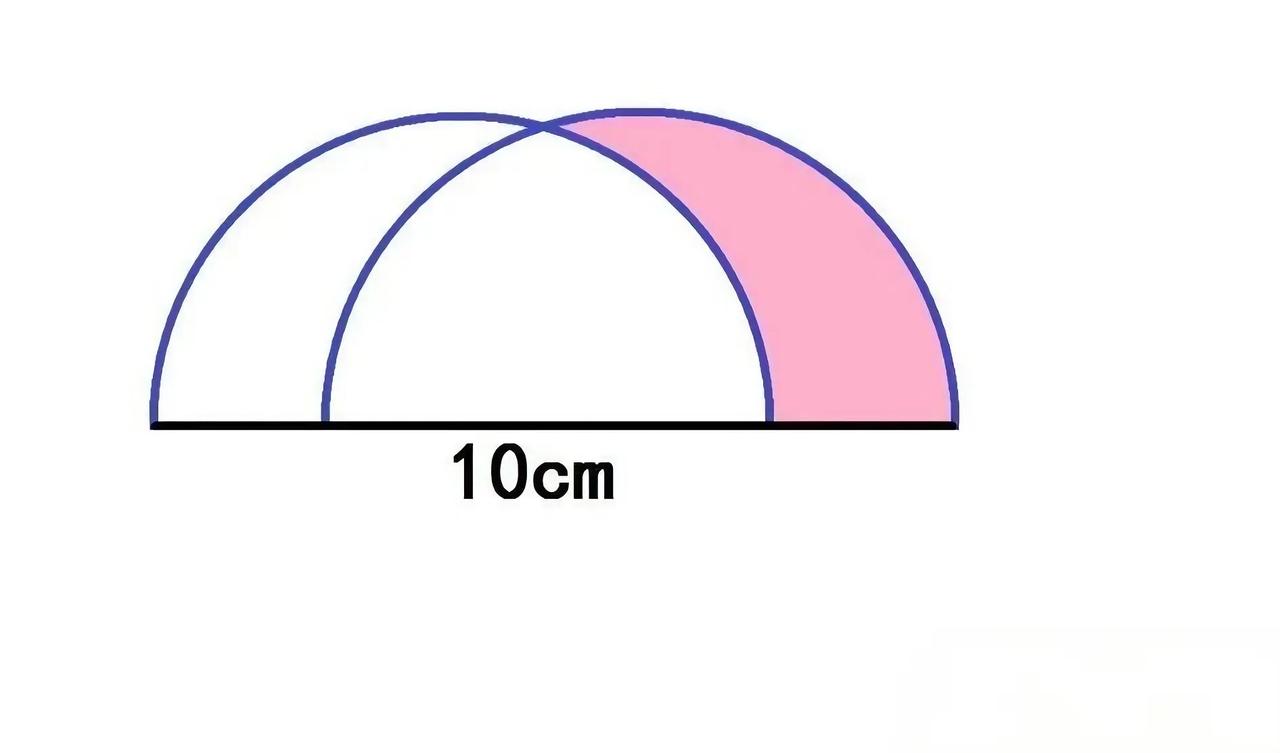
碰到这道几何题，第一眼被阴影区域搞得有点懵，但仔细琢磨后，发现解题关键藏在“变换”里。半圆右移2厘米后，阴影面积看似不规则，可几何的妙处就在于——不用死磕计算，换个思路，通过“等积变换”能让难题变简单。 想想看，图形的重叠、拼接里藏着规律，把阴影和周围的空白区域联系起来，会发现某些部分的面积是可以相互替代的。这就像给图形变魔术，把零散的阴影“转移”到一个更规则的形状里。 其实很多几何题都是这样，考验的不是计算力，而是对图形关系的洞察力。当你找到那层面积转化的窗户纸，阴影的秘密也就揭晓了，是不是觉得几何思维特别有意思？