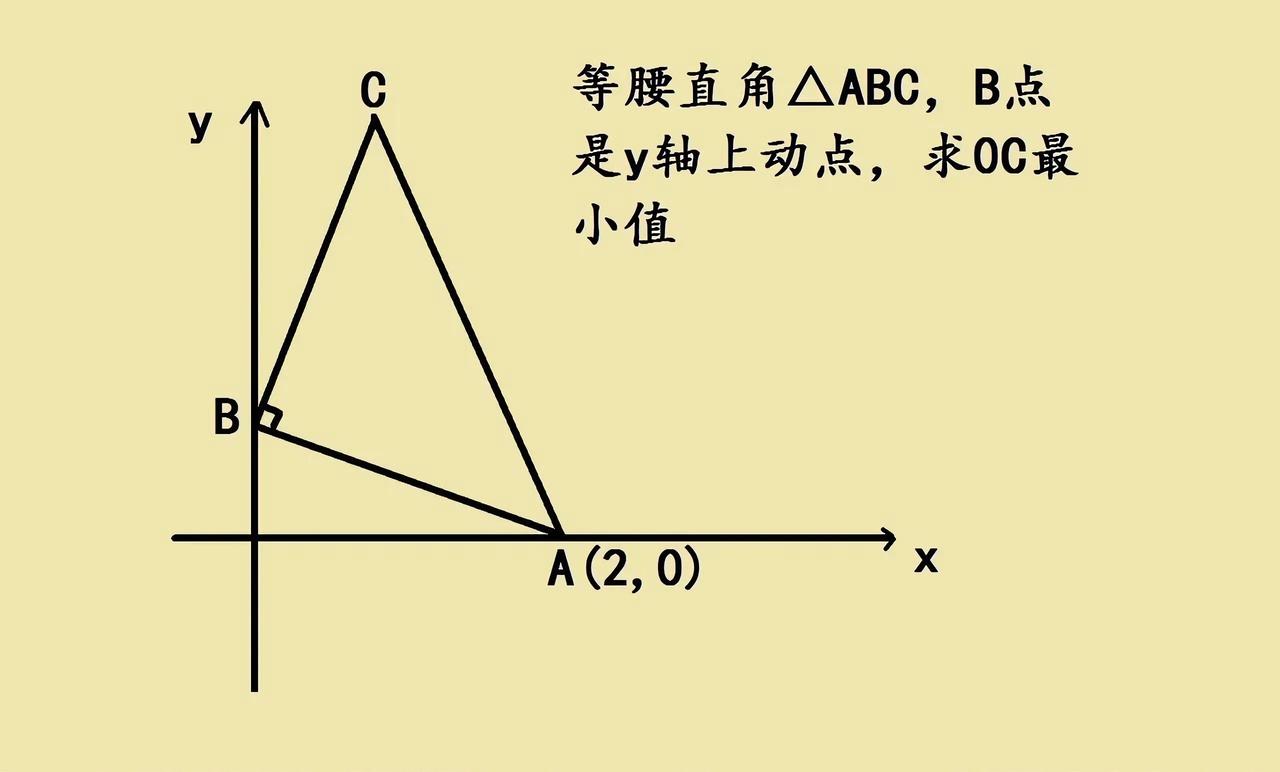
初中几何题难倒全家,关键思路在这里! 一道等腰直角△ABC的几何题,难住了女儿和大学生宝爸 。题中A点坐标(2,0),B在y轴动,求OC最小值。 这类动点求最值问题,核心是找轨迹!因为△ABC是等腰直角且∠B为直角,可通过“几何变换”找C点运动轨迹。比如,利用等腰直角三角形的旋转特性,把△ABO绕B点旋转,构造全等或特殊图形,就能发现C点轨迹是条直线或圆弧。 一旦确定C点轨迹,根据“点到直线(或圆)的距离,垂线段最短”,找到O到轨迹的最短距离,就是OC最小值 。初中几何动点最值,常考轨迹思想,掌握旋转、对称等变换,把动点转化为定轨迹,难题就迎刃而解啦~快试试用轨迹思路突破这道题!
评论列表