关于“数学是什么”以及“为什么世界时数学的”它究竟研究什么,一直存在许多争议。
或许有趣的是,大多数没有专业数学背景的人在面对“数学是学什么的”这一问题时,很难迅速给出明确的答案。
一个常见的回答是:数学研究模式。这种说法有一定道理。
例如,数字就是一种重要的模式,它们表示数量、面积、体积,以及增减和变化的过程。
如果问学生“数学是什么”,他们的第一反应多半是“数字”。
我们通常认为,如果未来人类与其他文明接触,彼此沟通的第一步可能就是分享彼此对数字的处理方式,因为数学是宇宙的语言,任何文明都应该遵守数学!
所以说,数字被看作普世的交流工具,但问题随之而来:这种文明是否使用我们熟悉的十进制系统?
答案未必。
我们使用十进制系统,或许仅仅因为人类有十根手指。
实际上,在我们的历史中,也曾经出现过十二进制系统。
这种系统的遗留痕迹在我们的日常生活中依然清晰可见,比如一天被划分为白天和夜晚,每段时长为12小时;每小时有60分钟,每分钟有60秒。
据说,这种计数方式源自人类通过手指关节计数——用拇指指向其他手指的12个关节。
那么,假如我们要向外星文明教授数学,又需要从何开始呢?
想像一下,假设有一天,人类真的遇见了外星文明。
眼前的外星生物可能完全没有共同的语言,也没有任何相似的文化背景——甚至他们的感官系统都可能和我们截然不同。
那么,我们该如何与他们进行交流?
答案或许可以归结为一件事:数学。
数学可能是跨越种族与星际界限的“宇宙语言”,因为它超越了语言的表达形式,建立在逻辑和模式的基础之上。
但问题来了:如何用数学开始与外星人对话?这看似简单,实则充满挑战。
第一步:确认共通的数学基础
数学交流的第一步,是找到双方认知的共通点。
在没有共同语言的情况下,最基本的数字概念可能是一个起点。
数字的表示方式:可以通过举例,展示数字的规律性。
比如,通过一组重复的信号(如闪光灯、声音、图案等)表示“1、2、3”,让外星人明白这些信号代表不同数量。
数列的模式:用一系列递增的数字,如“1、2、3、4”或者“2、4、6、8”,传递简单的加法或乘法概念。
如果外星人能够回应或者模仿,说明他们至少能够识别某种基础的数学模式。
第二步:用几何作为视觉语言

二维的几何图形
几何图形是另一种可能的数学沟通工具。我们可以用几何形状展示数学关系,因为这些图形不依赖特定的语言或文化背景。
基本形状:展示圆形、正方形、三角形等基本几何图形。通过数量和形状的变化,可以传递“1、2、3”等概念。
比值和比例:例如,通过展示正方形与圆形面积的关系,尝试传递“π”的概念。即使外星人不知道圆周率的具体数值,他们或许能够理解比例关系。
对称性和规律性:对称性是宇宙中广泛存在的一种美学和数学特性,可能是外星生物可以识别的通用模式。
第三步:寻找进制系统的共识
人类使用十进制是因为我们有十根手指,但外星文明的进制可能完全不同。
他们或许用二进制(更适合数字化文明)或十二进制(因为结构对称性)进行计算。
测试进制的理解:通过递增的数字模式,如“1、10、11(假设是二进制)”与“1、2、3、4、5、6……”(十进制)进行比较,看外星人的反应。
展示我们的进制:用实际物理对象,比如石子或光点,按“10”为单位进行分组,帮助他们理解我们使用十进制的逻辑。
第四步:用代数和模式传递逻辑
一旦确认基本的数学共识,可以尝试更复杂的概念,比如代数和函数。这一步可能需要通过示范来解释逻辑关系。
算术与方程:通过展示简单的加减法和乘法关系,比如“2 + 2 = 4”“3 × 3 = 9”,引导他们理解数字间的运算规则。
斐波那契数列:通过演示这种自然界中常见的模式,观察外星人是否能识别并回应这种规律。

以斐波那契数为边的正方形拼成的近似的黄金矩形(1:1.618)
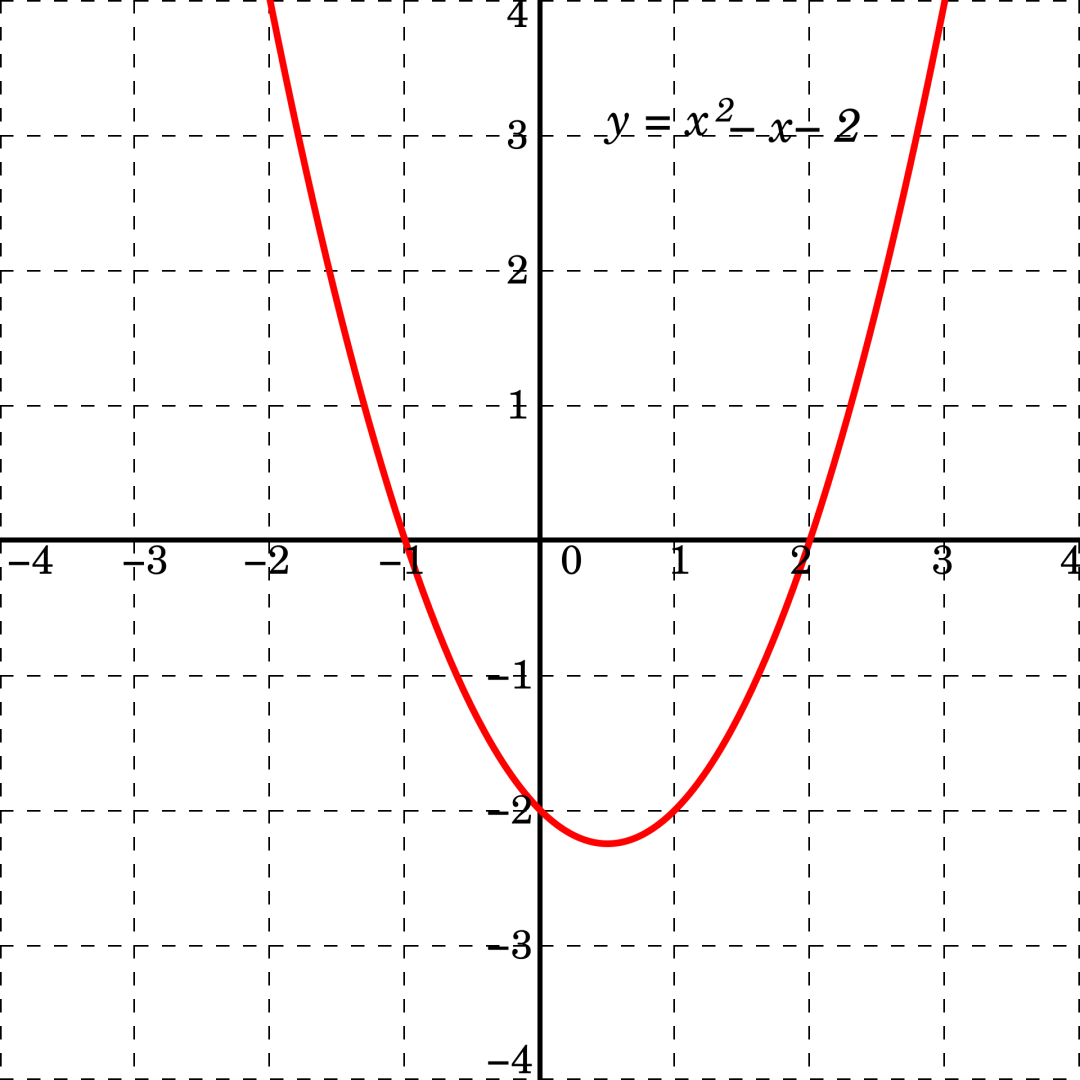
图形化表达函数:画出y = x^2或y = x + 1等简单图形,展示变量之间的关系。
第五步:讨论宇宙中的数学常量
数学交流的核心在于找到宇宙中普遍适用的常量和原理。例如:
圆周率(π):通过展示圆的直径与周长的关系,传递这一概念。
自然对数(e):在指数增长或者衰减现象中,这一常量可能与外星生命的科学经验相关。
黄金比例:这一比例广泛存在于自然界,可能也是外星人熟悉的规律。
如果外星文明也有科学研究的传统,他们或许对这些常量十分熟悉,甚至可能拥有我们尚未发现的数学常量。
第六步:尝试用数学探索物理世界
物理与数学密不可分。
通过展示物理现象中的数学规律,可以进一步加强沟通。
牛顿运动定律:用简化的形式展示“F = ma”的概念,或者以重力为例,用数学描述物体的加速度。
光的传播:用光线的反射、折射和速度关系解释光学定律。
天体运动:展示行星的公转轨迹和开普勒定律,尝试传递引力和轨道的数学描述。
这些现象不仅是数学的应用,也是宇宙的普遍规律,可能成为双方共同理解的基础。
假如外星人也有高等数学或逻辑的能力,可以尝试探讨更抽象的数学问题:
无穷”概念:讨论无限数列或者几何中的无穷,探索他们是否也有类似的数学思想。
数学与现实的关系:是否所有的数学原理都可以应用于现实,或者是否存在超越物理世界的数学维度?
总结:
数学不仅仅是一种工具,它更像是一种逻辑的“通用语言”。
通过数字、图形、模式和常量,我们有可能跨越语言和文化的鸿沟,与完全不同的生命形式建立联系。当然,这一过程并非易事,需要足够的耐心和创造力。
或许某一天,当人类真正遇到外星人时,我们第一句“你好”不会用语言表达,而是通过一组简单的数字序列——因为在浩瀚宇宙中,数学可能是唯一真正的“共同语言”。
评论列表