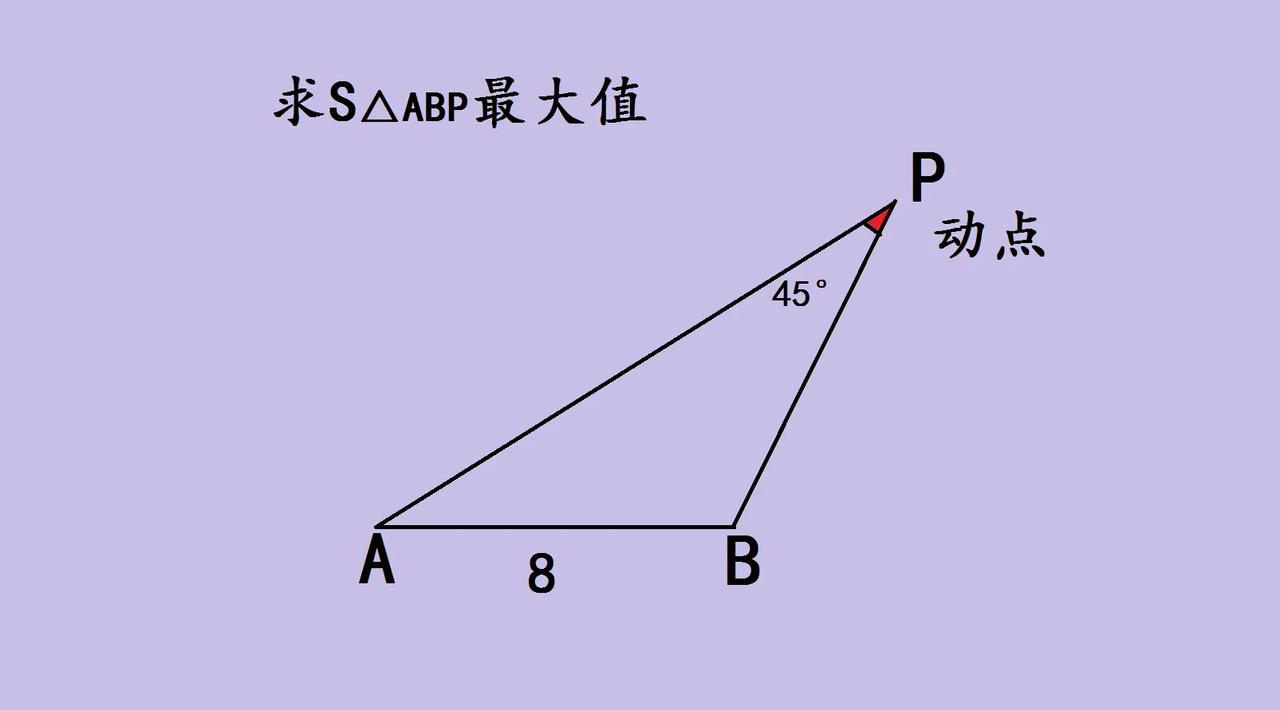
动点三角形面积最值,几何思维大挑战 家人们,来看这道超有意思的几何题!已知AB长8,动点P满足∠P始终是45°,求△ABP面积的最大值 。 首先,要求三角形面积,这里AB是底,长度固定为8,所以关键就是找AB边上的高的最大值! 因为∠P = 45°,这是个定值,P是动点,那可以想想P的运动轨迹。其实,P点的轨迹和圆有关(涉及圆周角定理,同弧所对圆周角相等 )。当高最大时,就是P到AB的距离最远的时候,结合这个45°角的条件,就能找到高的最大值,进而算出面积最大值。 这种动点几何题超锻炼空间思维,把定值角和动点轨迹结合,从“变”中找“不变”。学生做这类题,能加深对三角形面积、圆周角定理的理解,体会几何里的动态美和逻辑推导的乐趣,家长也可以和孩子一起琢磨,感受数学几何的奇妙,一起解锁解题思路~
评论列表