关于自然世界的最令人惊奇的事实之一是其中的许多实体（无论是生物实体还是纯物理实体）都遵循一组特定的模式和比例。许多星系都呈现出螺旋形状和结构，许多植物结构也是如此：其中包括球果、菠萝和向日葵头。菊石（6000 万年前灭绝的贝壳软体动物）也显示出这种螺旋图案，其中螺旋的一个关键特征是，前一圈之外的下一个“圈”与前一个圈的大小具有一定的长度比。

在任何此类结构中，该比率通常非常接近斐波那契数列中两个相邻数字的比率。这个数学序列通常教给孩子们，从数字“0”和“1”开始，然后通过将前两项相加得到序列中的下一项。它可能是最著名的数学序列，但是如何解释该序列的模式以及它是否真的与自然有着千丝万缕的联系？以下是 Ragtag Media 针对这个问题所写的内容：

“星系演化是否存在斐波那契数列？”

事实上，仅仅看星系中的“螺旋”结构可能看起来与斐波那契相似，但它是真实的，还是只是我们的大脑在仅存在明显联系的情况下创建了不必要的联系？

银河系和其他物理螺旋

就纯物理科学中自然发生的螺旋而言，“螺旋星系”无疑是其中最著名的。在所有已知的大型、附近的大质量星系中，有一半以上的星系内部都有螺旋形状和结构，但当我们用数学方法检查它们时，发现它们中很少有呈现出类似斐波那契模式的星系。

重要的是，类似斐波那契的模式被称为“自相似”，如果您缩小并在更大的范围内观察它，当您靠近较小的范围时，相同的结构模式会重复。星系中看到的螺旋结构不会这样做，原因有两个：

螺旋星系的螺旋很少会一直延伸到中心，而是以不对称的星系驼峰或棒状结束

这些星系的外部部分——其中的恒星、气体和尘埃主要局限于星系盘中——用圆的曲线比用任何“向外螺旋”结构更好地近似。

星系内的旋臂是由密度波和星系随着时间的推移而“卷曲”引起的。一些螺旋星系中存在一些值得注意的特征，这些特征在这些中间区域表现出类似斐波那契的模式，但这些并不是常态。

尽管一些精心设计的螺旋星系可能具有看起来遵循斐波那契模式的特征，但这并不代表大多数螺旋星系，甚至也不代表几乎遵循这种模式的星系内的大多数特征。虽然斐波那契数列确实在许多地方可靠地出现，但螺旋星系并不是其中之一

少数确实显示出类似斐波那契模式的螺旋是一类被称为“精心设计的螺旋星系”的螺旋的一部分，这些螺旋仅占螺旋星系的十分之一，而不是最常见的多臂螺旋类型（包括银河系）和第二种最常见的类型，具有薄的多层螺旋结构，称为蓬松螺旋星系。这些“精心设计”的螺旋几乎都是最近经历过或正在经历与附近卫星星系的引力相互作用的星系，正是这种外部引力影响将最外面的旋臂和特征拉成与所发现的关系更一致的形状在斐波那契数列中。

虽然许多螺旋形状源于自然界中纯粹的物理、非生物过程——从水体中形成的漩涡和漩涡到飓风云和清晰路径的空气形式——但当涉及到实际的情况时，这些螺旋都不是斐波那契式的。数学不断地详细描述它们的结构。您可以拍摄“快照”，其中一个或多个特征表现出与斐波那契数列中某一点的关系一致的关系，但这些模式无法维持或持续。螺旋星系中看到的斐波那契式模式是我们眼睛的发明，而不是宇宙的物理真相。

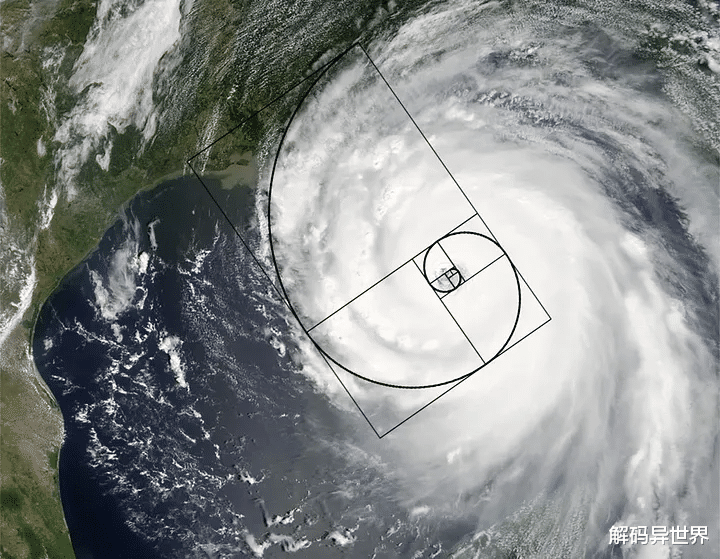
这张卡特里娜飓风的卫星图像似乎显示了其云层的螺旋结构。虽然将这种模式与斐波那契螺旋进行比较可能很诱人，但这种关联是有争议的，因为这种模式和大多数飓风都没有遵循黄金比例的螺旋模式

然而，在包括植物在内的许多生物有机体中发现的类似斐波那契的模式和关系确实与斐波那契数列有关：无论是在严格的数学意义上，还是出于完全合理的进化原因。让我们先看看生物学特性，然后再回到数学。

从生物学角度来说，想象你是一株植物：一株原始植物。您有能力从阳光、土壤养分、水和二氧化碳中产生自己的能量，并通过叶子中发生的光合作用产生糖（储存的能量）。当你从种子中发芽时，你需要暴露叶子，而在你的遗传密码中的某个地方，将会有信息告诉你相对于前一片叶子以什么角度暴露你的“下一片叶子”。

您可以采用三叶草等植物所采取的简单路线，只需将三片叶子彼此成 120° 角排列即可：创建一个三角形图案。这条路径的问题在于它高效，但不可扩展。我们没有巨大的三叶草树，因为你无法“缩放”它：当你将三片叶子以 120° 角排列时，就没有地方放置“下一片”叶子，而“下一片”叶子也不会被阻挡得很厉害。有效地阻挡先前的叶子，或者不会有效地阻挡先前的叶子收集阳光。

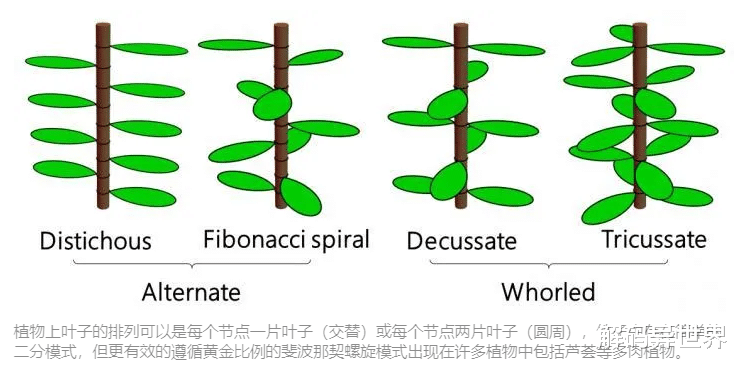
但是，如果您想根据上一张纸的放置位置编写最有效的方式来放置“下一张纸”，该怎么办？当然，对于总共三片叶子来说，120° 在数学上是理想的，但对于任意数量的叶子来说，这没有帮助。想象一下，你是一棵向上生长的植物，刚刚长出了第一片叶子。当它向上生长和第二片叶子的位置时，它应该以什么角度伸出，以便不仅第一片和第二片叶子，而且第三、第四、第五、第六等都接收到最大量的阳光一旦他们都就位？？

答案是，对于每张纸，下一张纸应与上一张纸对齐约整圆的 61.8%。对于 360° 的圆，这对应于 222.5° 的角度，而这对应的确切数字被数学家定义为 –ψ，等于 (√5–1)/2，或大约为 0.61803398875。其正版本 (√5 + 1)/2 称为 φ 或黄金比例，为 1/(-ψ)，也等于 1 + (-ψ)：每个斐波那契数及其前身。如果您继续以与前一片叶子成 222.5° 的关键角度暴露叶子，您最终会得到形成斐波那契螺旋的叶子图案。菠萝、松果等中编码的相同数学特性解释了为什么生物有机体经常显示斐波那契数列中的数字。

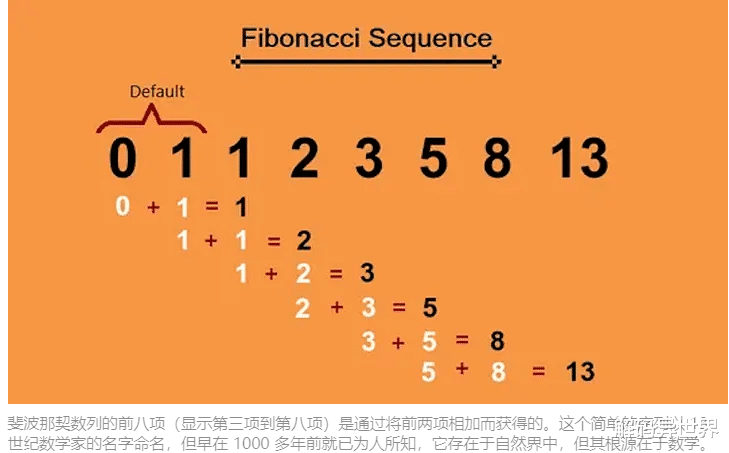
但最大的问题不是“为什么在自然界中存在斐波那契数列”，而是“首先是什么定义了斐波那契数列”？计算斐波那契数相当容易；您所要做的就是从前两个数字：“0”和“1”开始，然后将前两项相加得出下一项。斐波那契数列的前几项将是：

0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765 等，您可以在其中检查每个后续的可以通过查看前两个术语来获得术语。

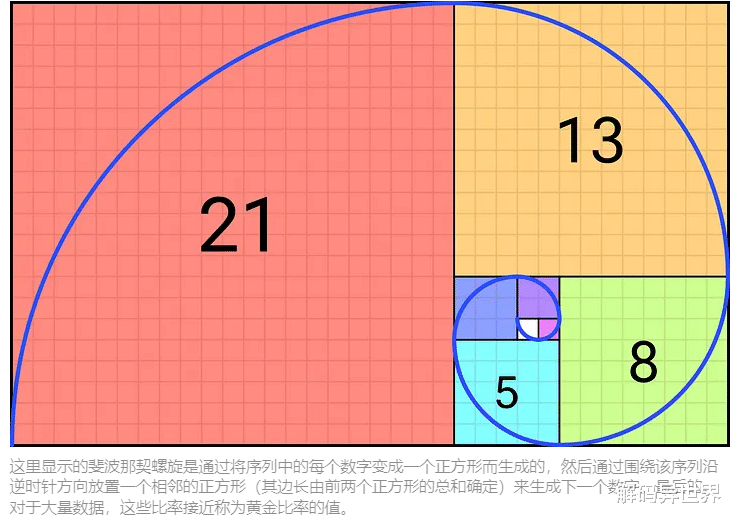
现在让我们看看任意两个连续项之间的比率，并从序列中的两个“1”开始，找出“下一项”与“前一项”的比率（所以我们不最终陷入被零除的情况）。

1 ÷ 1 = 1.0，

2 ÷ 1 = 2.0，

3 ÷ 2 = 1.5，

5 ÷ 3 = 1.66666…,

8 ÷ 5 = 1.6，

13 ÷ 8 = 1.625，

21 ÷ 13 = 1.61538462…,

34 ÷ 21 = 1.61904762…,

等等。

正如您所看到的，这些项在略小于黄金比例 φ（黄金比例）和略大于 φ 之间波动，但随着我们转向越来越大的项，无论是在上面还是在下面，都越来越接近它。

如果我们看一下上面写的最后三个数字 - 2584、4181 和 6765 - 您可以看到比率是：

4181 ÷ 2584 = 1.61803405573，以及

6765 ÷ 4181 = 1.61803396317，

非常快且非常接近黄金比例 φ 本身。如果我们向上移动几个数字，到 10946、17711、28657、46368，然后是 75025（100,000 以下的最后一个斐波那契数），我们会发现该比率为 75025 ÷ 46368 = 1.61803398896：黄金比例的估计值仅当扩展到第 11 个有效字符时才会有所不同。

事实证明，斐波那契数列的起点并没有什么特别之处。您可以从任意两个您喜欢的非负数开始，其中至少一个不为零：它们不必是“0”和“1”，它们不必是整数，它们不需要朋友之间不一定要很亲近。您所要做的就是遵循相同的公式，将前两个数字加在一起以获得下一个（第三个）数字，然后将该数字添加到前一个数字以获得下一个后续数字，依此类推。无论你从什么数字开始，任何两个连续数字的比率都会很快接近黄金比例 φ。

这让我想知道：是否有一种方法可以简单地生成任何和所有斐波那契数，而不必诉诸对前面的每一项求和来实现？事实证明确实存在，而且这是令人难以置信的数学好奇心。不管你信不信，关键是斐波那契数列中的第 11 个数字：89。

89这个数字有什么特别之处？乍一看，没那么多。它所涉及的两个比率，89 ÷ 55 和 144 ÷ 89，似乎并不特殊：它们分别等于 1.6181818... 和 1.6179775...。但如果您采用完全不同的比率，即数字 1 与数字 89，您会发现有些奇怪的情况。如果你把它写成扩展小数，你会发现斐波那契数列的前几个数字只是简单地出现并且按顺序出现。

1/89 = 0.011235955…,

其中我们可以很容易地看到前几个可识别的数字：0、1、1、2、3和5。您可能会看到“9”并认为那里出了问题，但请记住接下来的两个数字是8和13，所以我们涉及某种“结转”，如果我们正确地进行加法，可以将我们希望的“8”变成“9”。然后我们可以使用一个巧妙的技巧来更广泛地检查斐波那契模式。

我们不要使用数字 89，而是记住我们使用的是十进制，因此可以在数字 89 的两侧添加“9”来创建分数 1/9899。当我们将其扩展到更多数字时，我们发现它的十进制扩展如下：

1/9899 = 0.0001010203050813213455…,

突然我们看到更多的斐波那契数列出现。如果我们尝试在两边都添加几个 9 会怎么样？例如，1/99989999？现在十进制展开变成：

1/99989999 = 0.00000001000100020003000500080013002100340055008901440233037706100987159725844181…,

我们看到越来越多的成员在遇到“结转”错误之前出现。在分母两边加上超过 9，你就有了一个生成斐波那契数的公式，按顺序出现在你的分数中，只要你敢扩展它。您可以简单地读出数字，然后在分数的分母两侧添加任意数量的 9（等量），小数扩展将为您提供所有斐波那契数，保证，其中的位数少于分数分母两边“9”的个数。

但这一切都回到“89”是有深刻原因的。想象一下，我们通过将斐波那契数列中的每一项除以 10^(n+1) 来求和，其中 n 是该项的数量。换句话说，这意味着我们的加法序列如下所示：

0.0 + 0.01 + 0.001 + 0.0002 + 0.00003 + 0.000005 + 0.0000008 + 0.00000013 + 0.000000021 + 0.0000000034 + 0.00000000055 + 0.00000000008 9 + 0.0000000000144 + ...,

等等。现在让我们做一个小数学技巧：将此序列乘以 10，然后从中减去原始序列（得到原始序列的九倍）。它看起来像这样（忽略第一项，它为零）：

0.1+0.01+0.002+0.0003+0.00005+0.000008+0.0000013+0.00000021+0.000000034+0.0000000055+0.00000000089+0.00000000014 4 + … — (0 .01 + 0.001 + 0.0002 + 0.00003 + 0.000005 + 0.0000008 + 0.00000013 + 0.000000021 + 0.0000000034 + 0.00000000055 + 0.000000000089 + 0.0 000000000144 + …),

如果我们单独取第一项，然后将每个后续项组合在一起，则得出：

0.1 + (0 + 0.001 + 0.0001 + 0.00002 + 0.000003 + 0.0000005 + 0.00000008 + 0.000000013 + ...) 这告诉我们，原序列的九倍是0.1 + 原序列的十分之一！

或者换句话说，原始数列，即斐波那契数列中按小数位排序的数字之和等于0.1/8.9，即1/89。这就是为什么斐波那契数列不是自然界固有的，而是纯数学固有的。它出现在自然界中是因为黄金比例具有生物学上的好处，但无论它出现在物理科学中，包括在一些螺旋星系中，它都只是纯粹的巧合！