本文主要介绍复合函数y=(x+1)^3的定义域、值域、单调性、凸凹性及极限等性质,并简要画出函数图像示意图。

因为y=(x+1)^3,可知函数为幂函数的复合函数,根据函数特征,自变量x可以取任意实数,所以函数的定义域为:(-∞,+∞)。
函数单调性:用导数知识判断函数的单调性,主要步骤如下:
∵y=(x+1)^3,
∴dy/dx=3(x+1)^2>0,
即函数y在定义上为单调增函数。
从复合函数角度来分析,函数y可以看做为一次函数u=x+1和幂函数y1=u^3复合而成,其中在定义上,一次函数u=x+1为增函数,幂函数y1=u^3也为增函数,所以其复合函数y=(x+1)^3为增函数。

因为dy/dx=3(x+1)^2,
所以d^2y/dx^2
=3*2*(x+1)
=6(x+1).
令d^2y/dx^2=0,则x+1=0,即x=-1.
(1)当x∈(-∞,-1]时,d^2y/dx^2<0,函数为凸函数。
(2)当x∈(-1,+∞)时,d^2y/dx^2>0,函数为凹函数。
函数极限:Lim(x→-∞) (x+1)^3=-∞;
Lim(x→+∞) (x+1)^3=+∞;
可见,函数的值域为(-∞,+∞)。
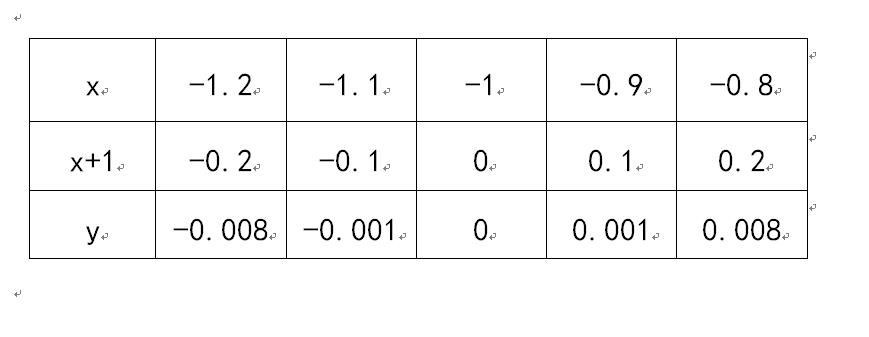
函数五点图: