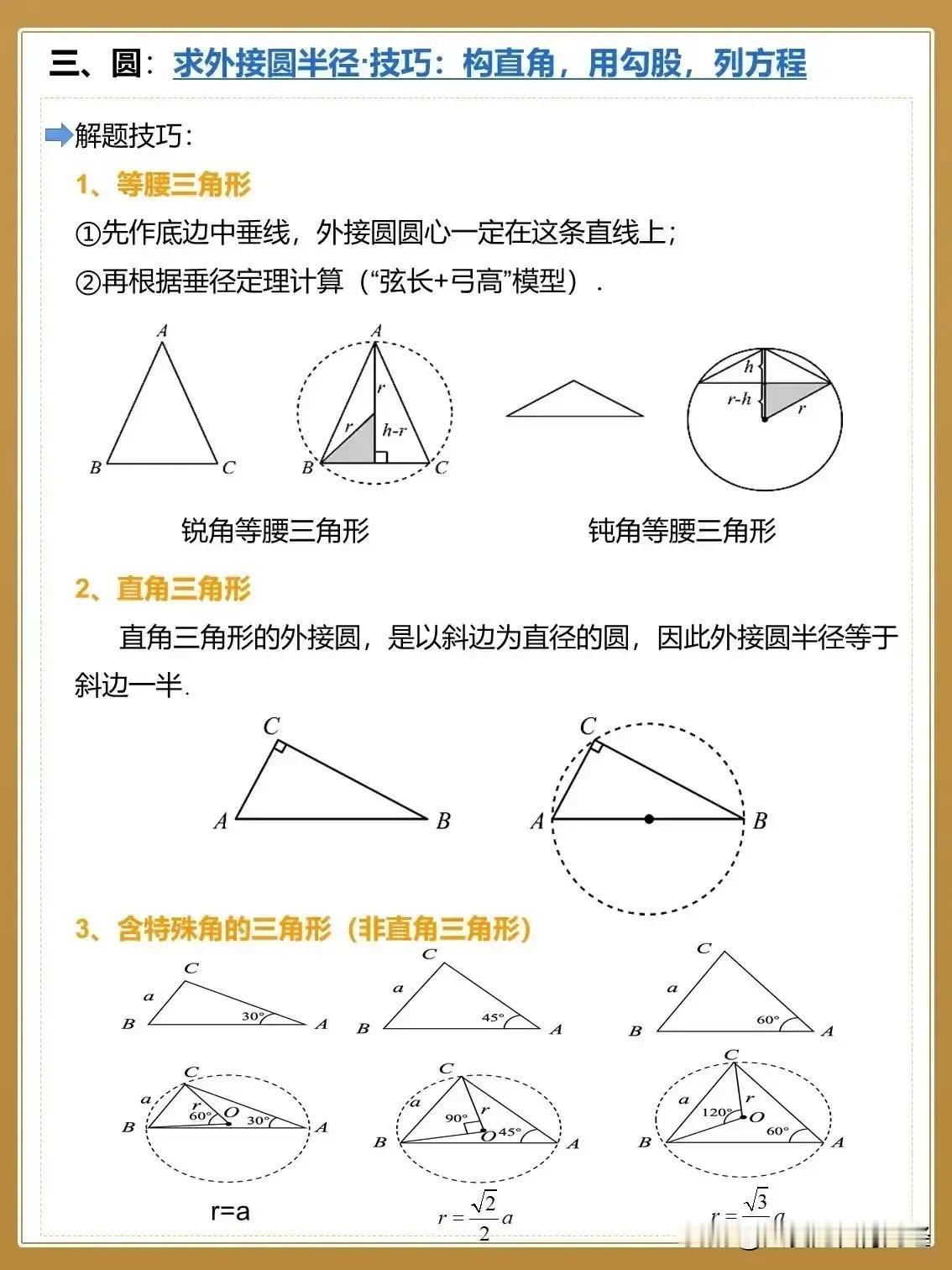
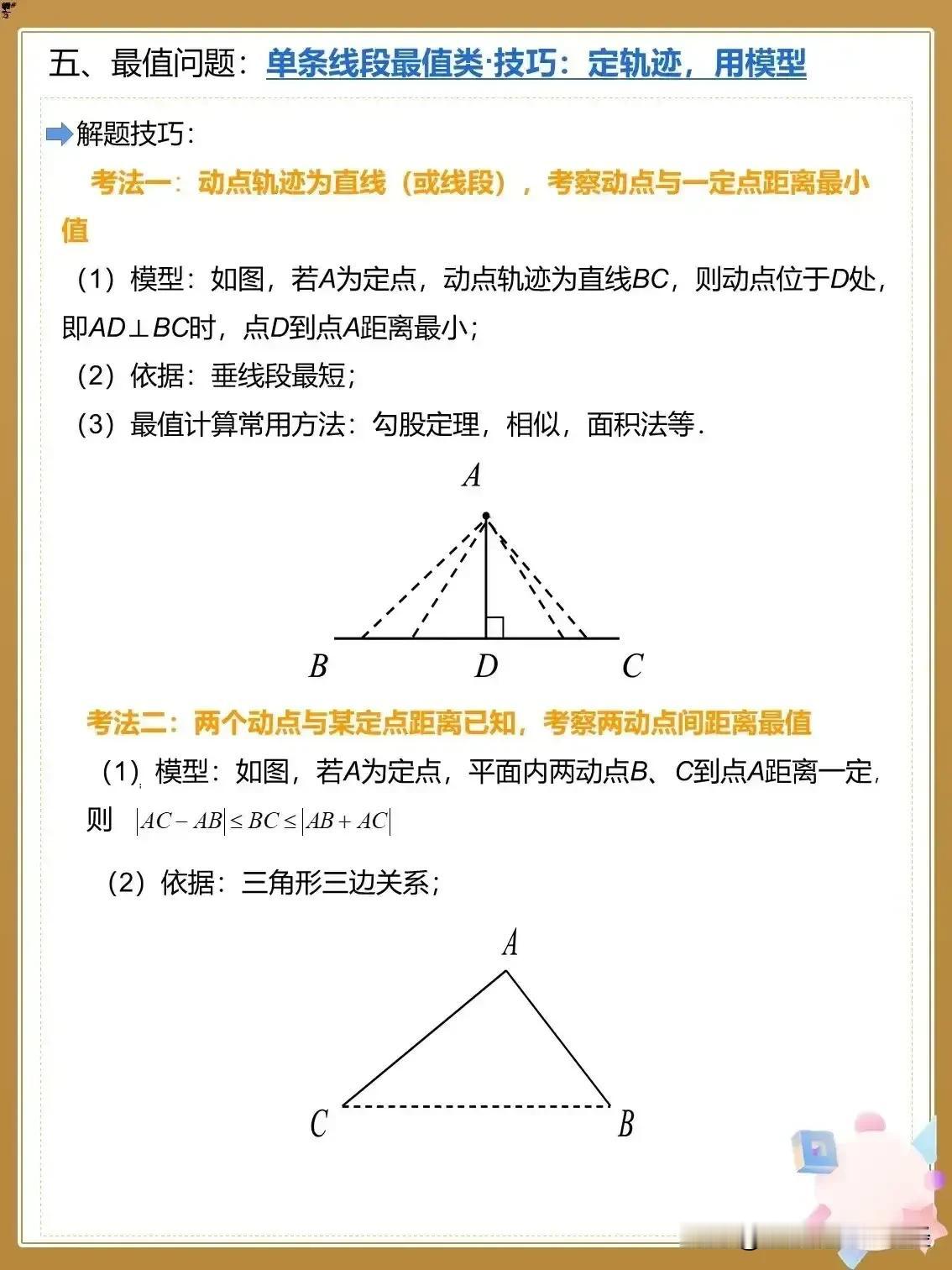
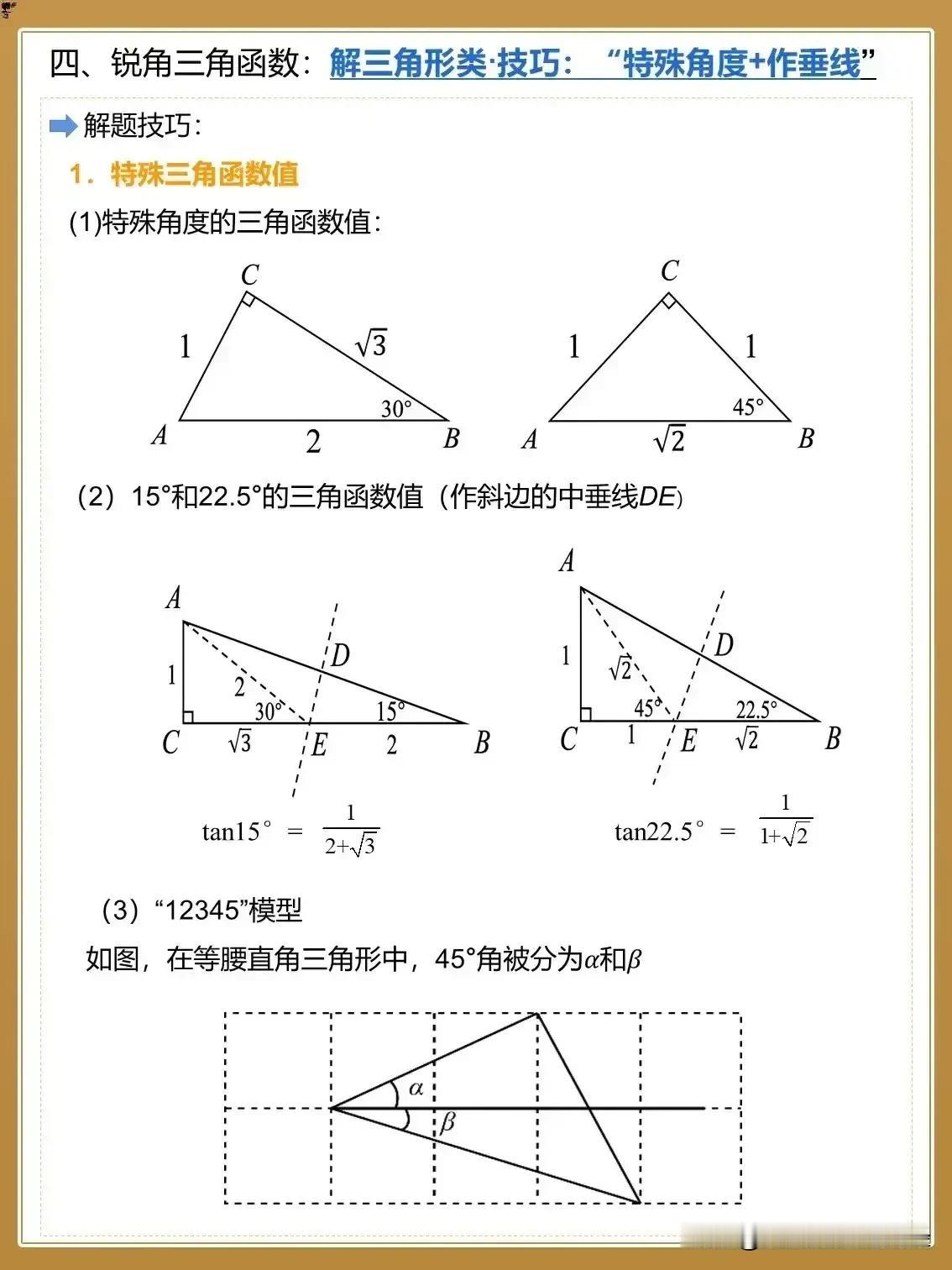
看完这八张图，我才恍然大悟，原来初中数学几何模型有60种解题技巧，什么折叠问题，求证乘积式，最值问题，三角函数等全都整理得清清楚楚明明白白，看完后，彻底被征服了。背下来，孩子的初中数学就稳了！ 先来看看折叠问题。在几何中，折叠往往意味着图形的对称与变换，而这类问题常常让学生感到无从下手。但在这张图中，一种巧妙的辅助线画法让我豁然开朗。 例如，面对一个折叠后的三角形，通过连接折叠前后的对应点，并作出对称轴，原本复杂的图形瞬间变得清晰明了。再配合上相似三角形的性质，折叠问题便迎刃而解。这种方法的妙处在于，它不仅仅解决了当前的问题，更让我对图形的对称性质有了更深的理解。 接下来是求证乘积式的问题。这类问题往往需要我们证明两个线段的乘积等于另外两个线段的乘积，看似简单，实则暗藏玄机。图中展示了一种通过构造相似三角形来求解的方法。 以一道经典题目为例：在直角三角形中，斜边上的中线与直角边构成的两个三角形是相似的。利用这一性质，我们可以轻松地找到证明乘积式的关键线索。这种方法不仅简洁明了，而且让我对相似三角形的应用有了更深刻的认识。 最值问题一直是几何中的难点之一。如何找到图形中的最大或最小值，往往需要我们综合运用多种几何知识。在这张图中，我看到了一种通过构造辅助圆来求解最值问题的方法。 例如，在一个给定的线段上找一个点，使得该点到线段两端点的距离之和最小。通过构造以线段两端点为焦点的椭圆，并找到与给定线段相切的切点，我们便能轻松地找到这个最值点。这种方法的巧妙之处在于，它将几何问题转化为了代数问题，让我们能够更直观地看到问题的本质。 当然，几何的学习离不开三角函数的支持。在这张图中，我看到了一种通过三角函数来求解几何问题的方法。例如，在一个直角三角形中，已知两条直角边的长度，要求斜边的长度。 这时，我们可以利用勾股定理来求解，但更巧妙的是，我们还可以通过正弦、余弦等三角函数来求解。这种方法不仅让我们对三角函数有了更深的理解，也让我们看到了几何与代数之间的紧密联系。 除了以上提到的几种几何模型外，这八张图中还涵盖了其他多种几何模型，如平行线模型、圆与直线的关系模型等。每一种模型都通过详细的图形和解题技巧进行了展示，让我对几何的理解更加全面和深入。 例如，在平行线模型中，我看到了如何通过平行线的性质来求解角度和线段长度的问题；在圆与直线的关系模型中，我学到了如何通过构造垂径线来求解圆与直线的问题。 通过学习这八张图，我深刻体会到了几何的魅力与奥秘。每一种解题技巧都蕴含着深厚的几何原理，而掌握这些技巧，不仅能够帮助我们解决考试中的难题，更能够让我们对几何世界有更深刻的认识。同时，我也意识到，学习几何并不仅仅是掌握一些解题技巧，更重要的是培养我们的逻辑思维能力和空间想象能力。 对于家长和孩子们来说，这八张图是一份宝贵的学习资料。它不仅能够帮助孩子们掌握几何的解题技巧，更能够激发他们对几何的兴趣和热情。因此，我建议家长们将这份资料保存下来，有空时拿给孩子们学一学。只要孩子们能够把这些知识点理解透了，考试轻松拿高分将不再是难事！ 初中数学几何辅助线