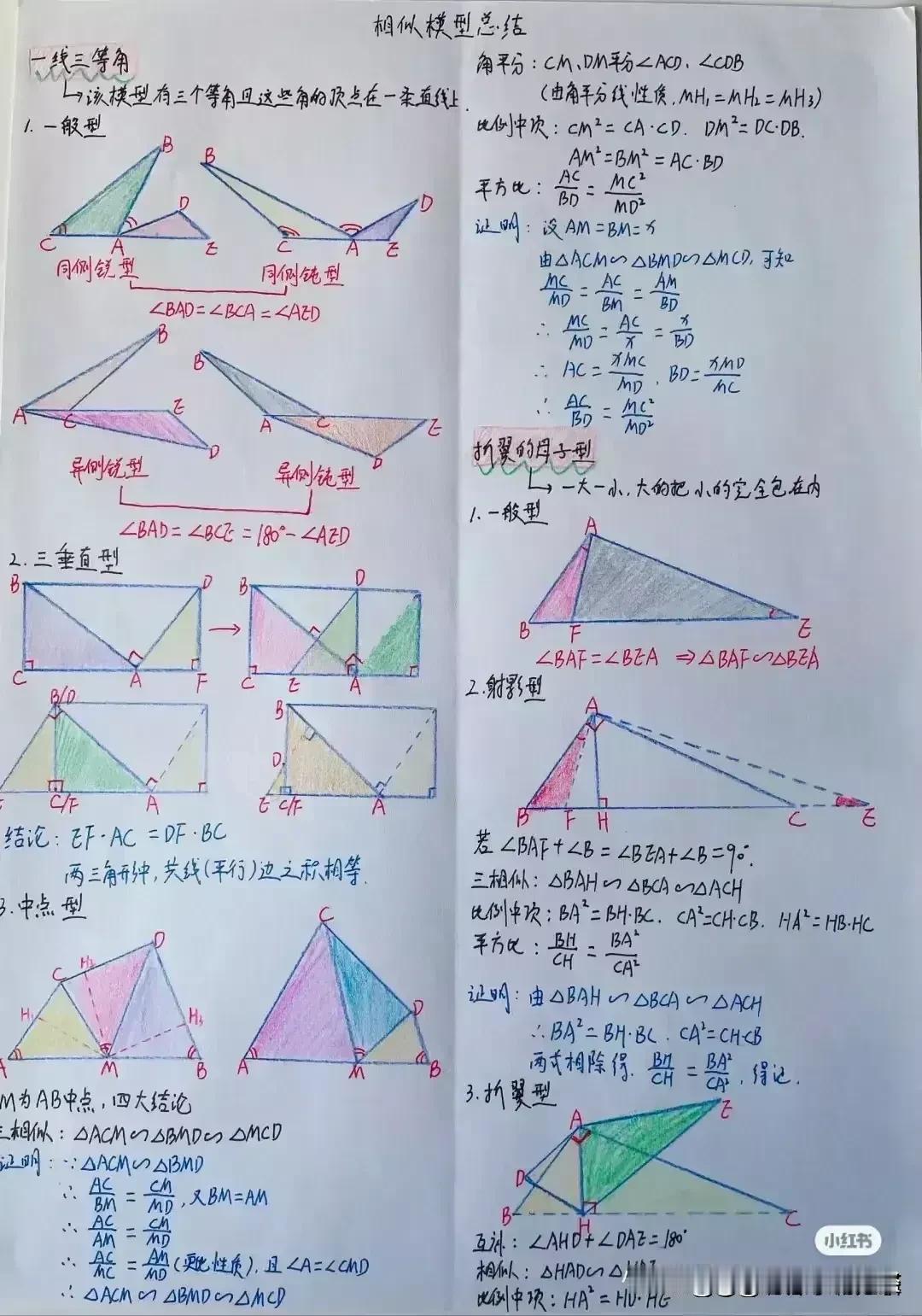
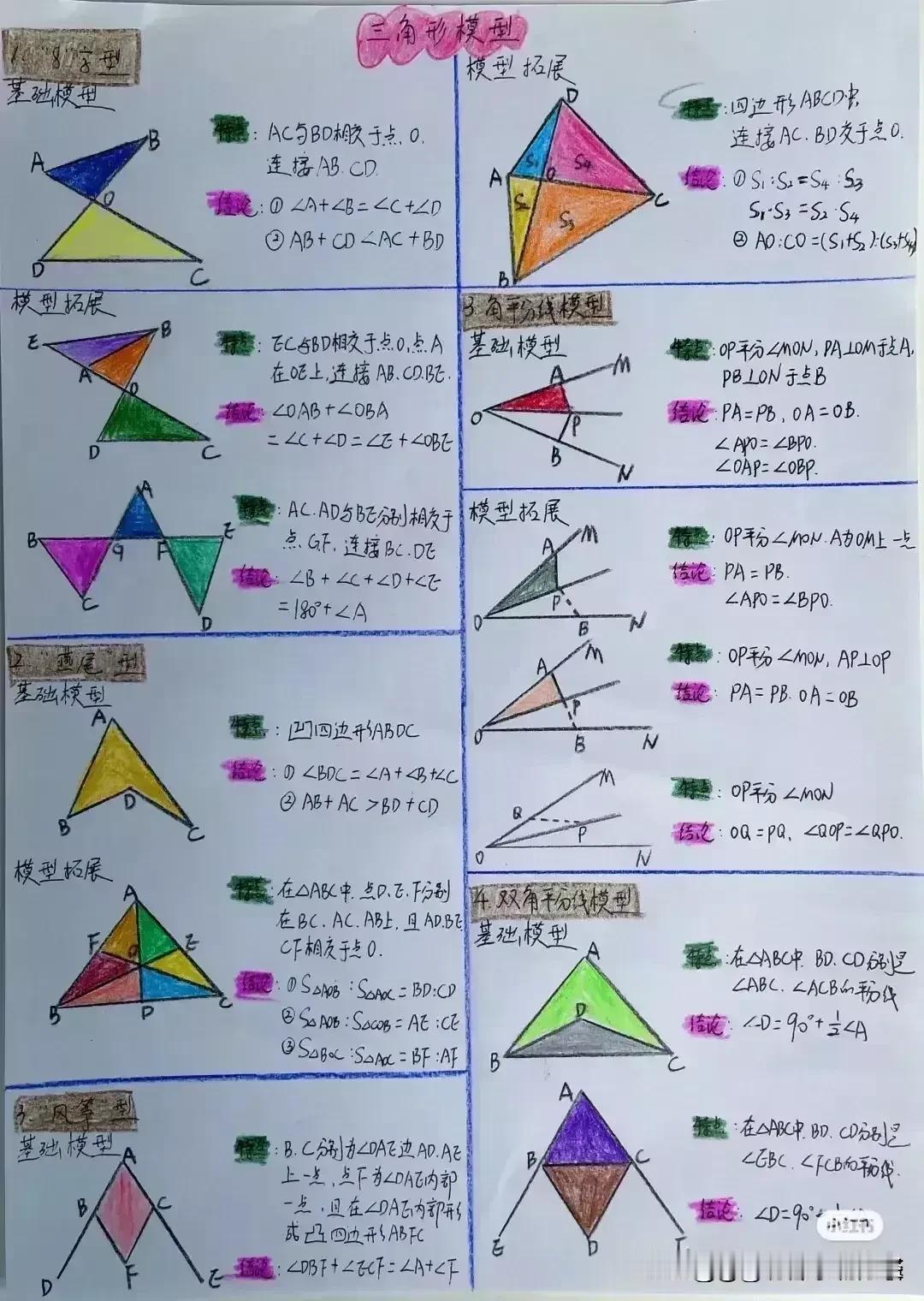
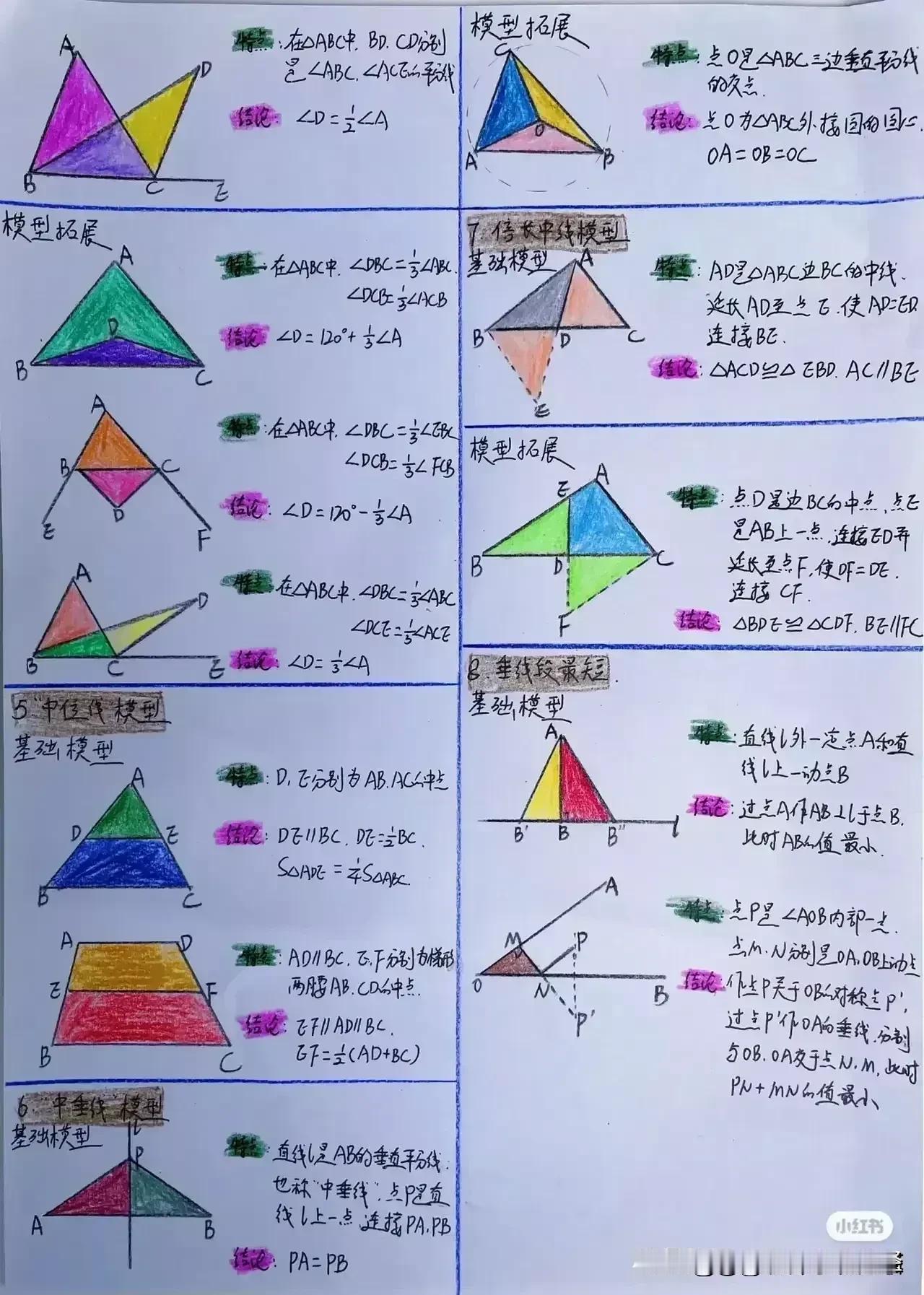
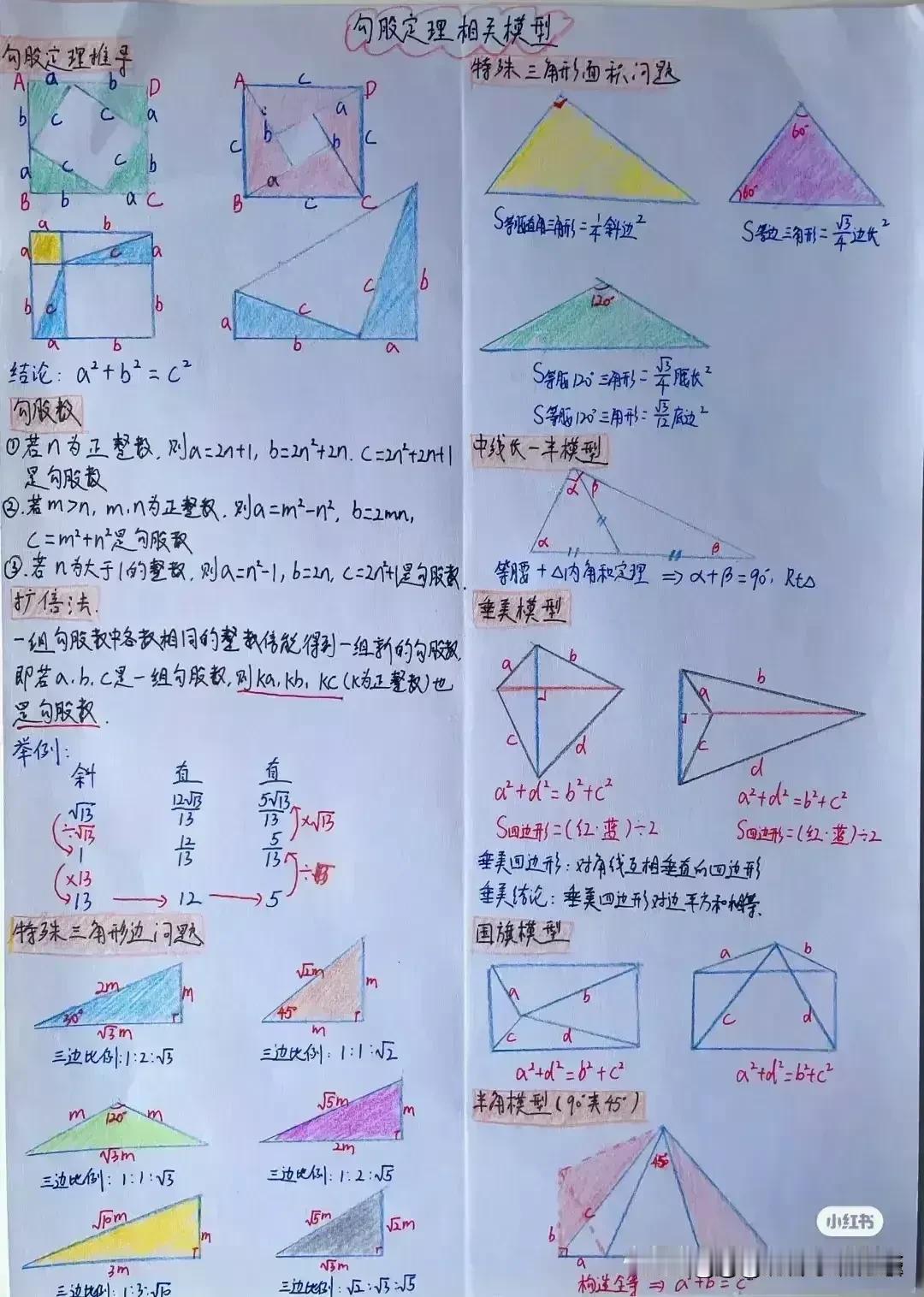
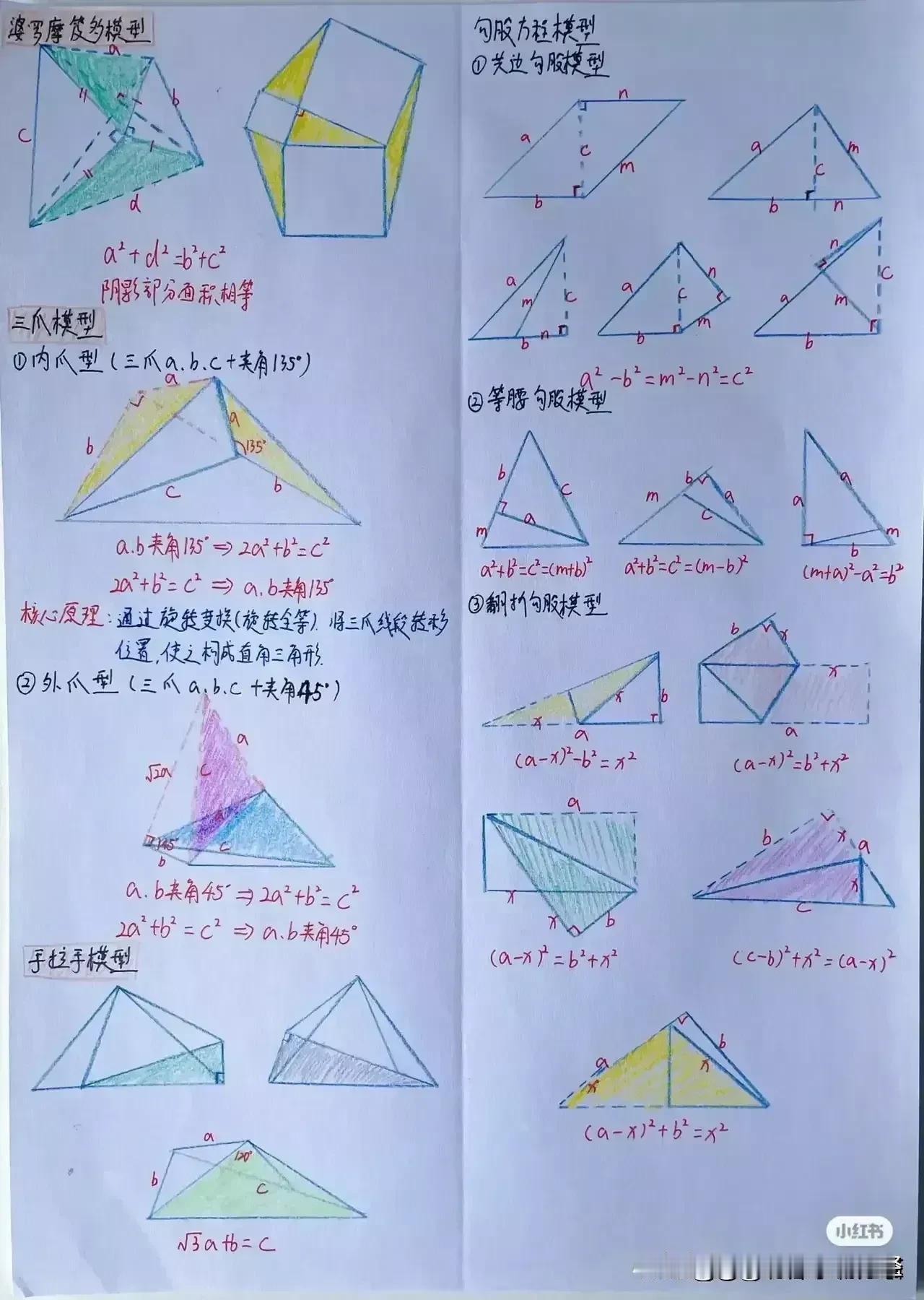
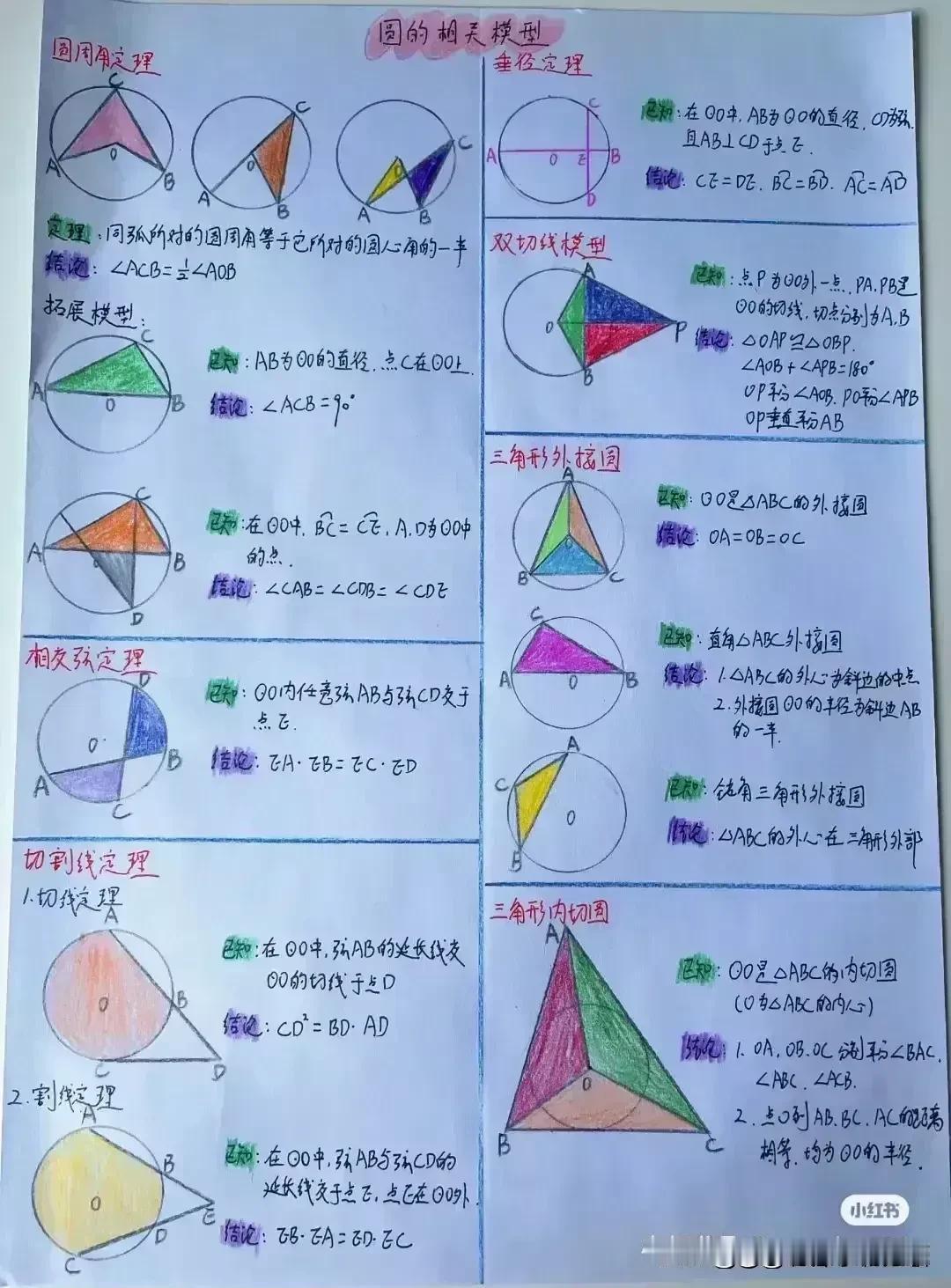
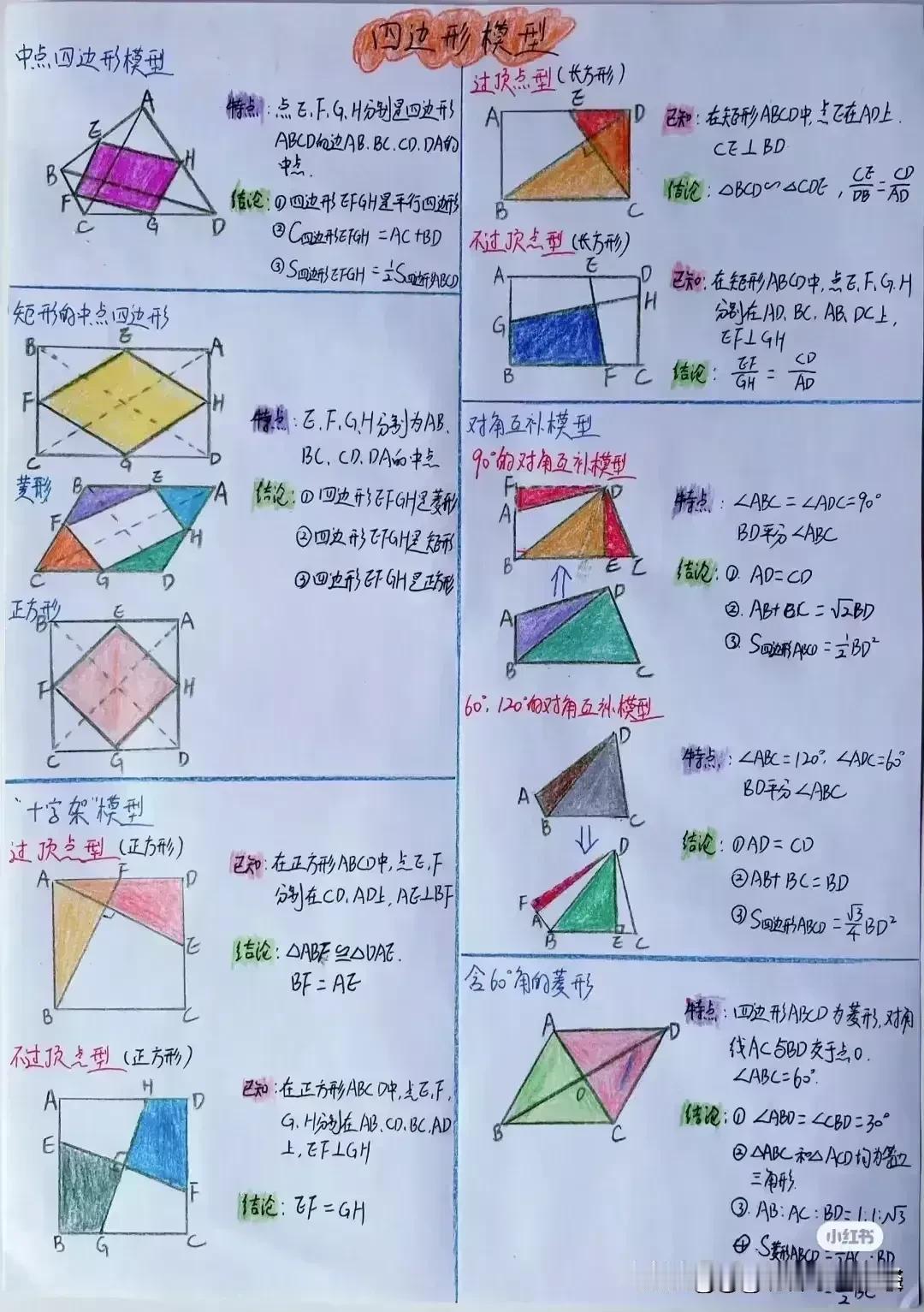
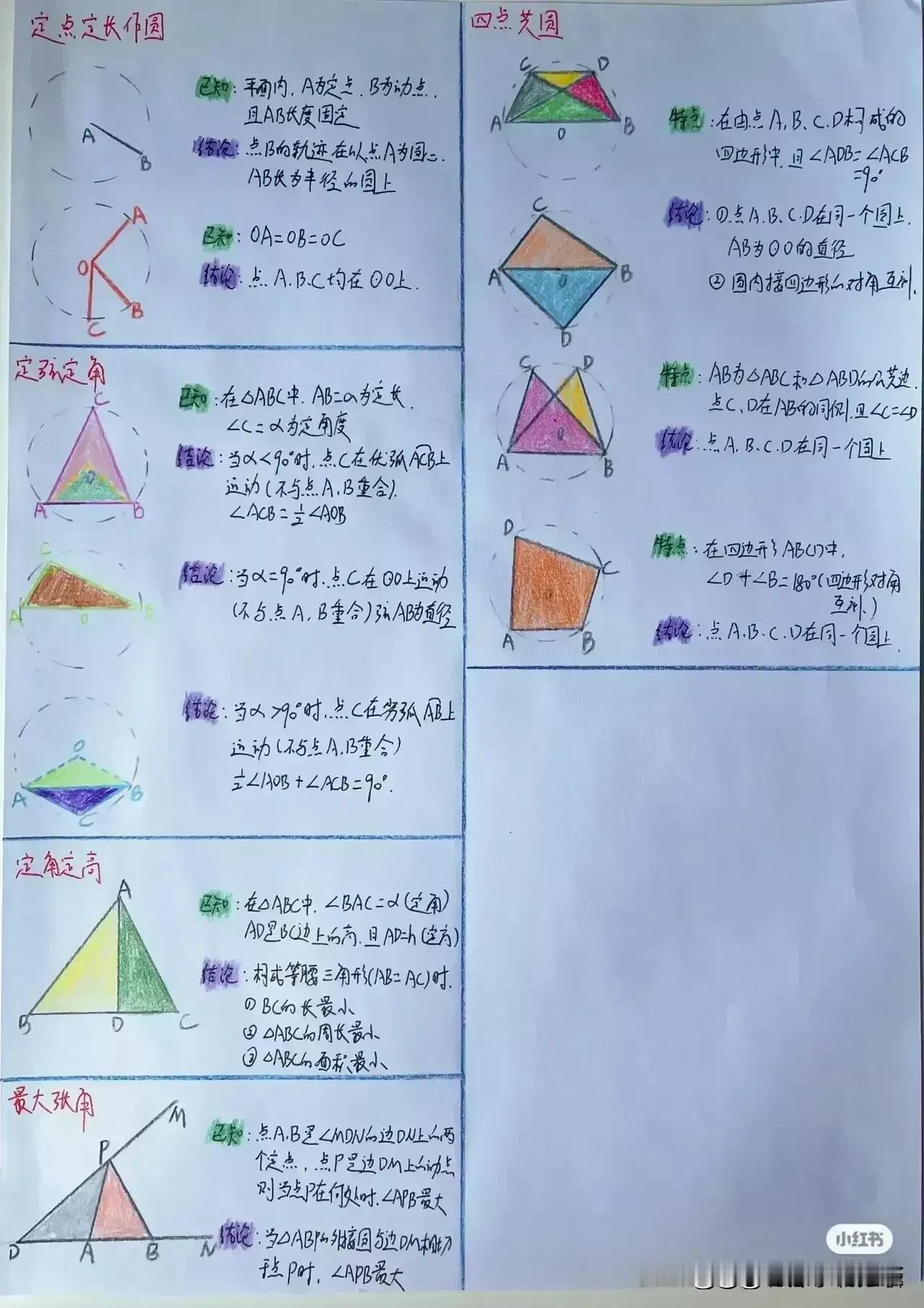
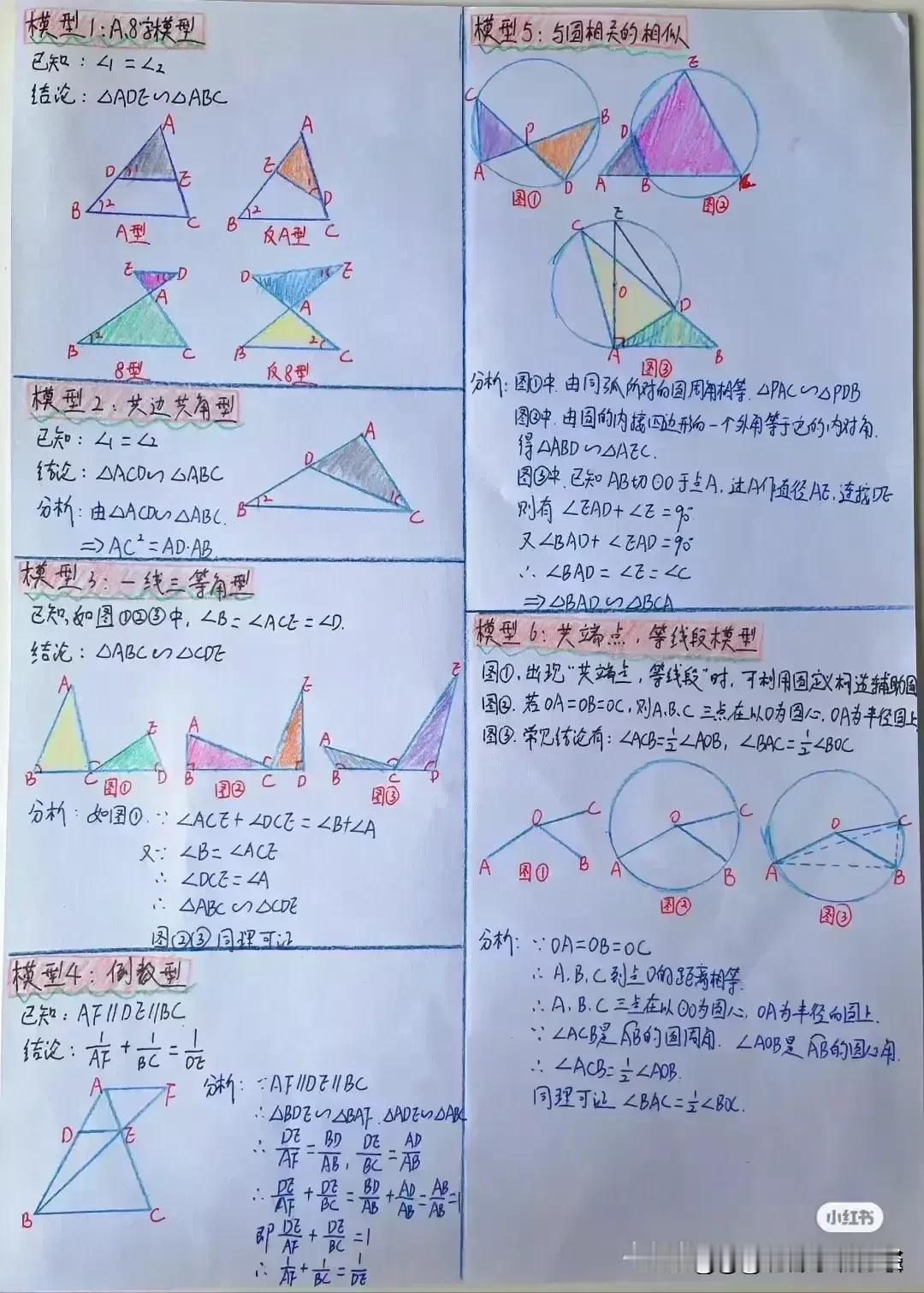
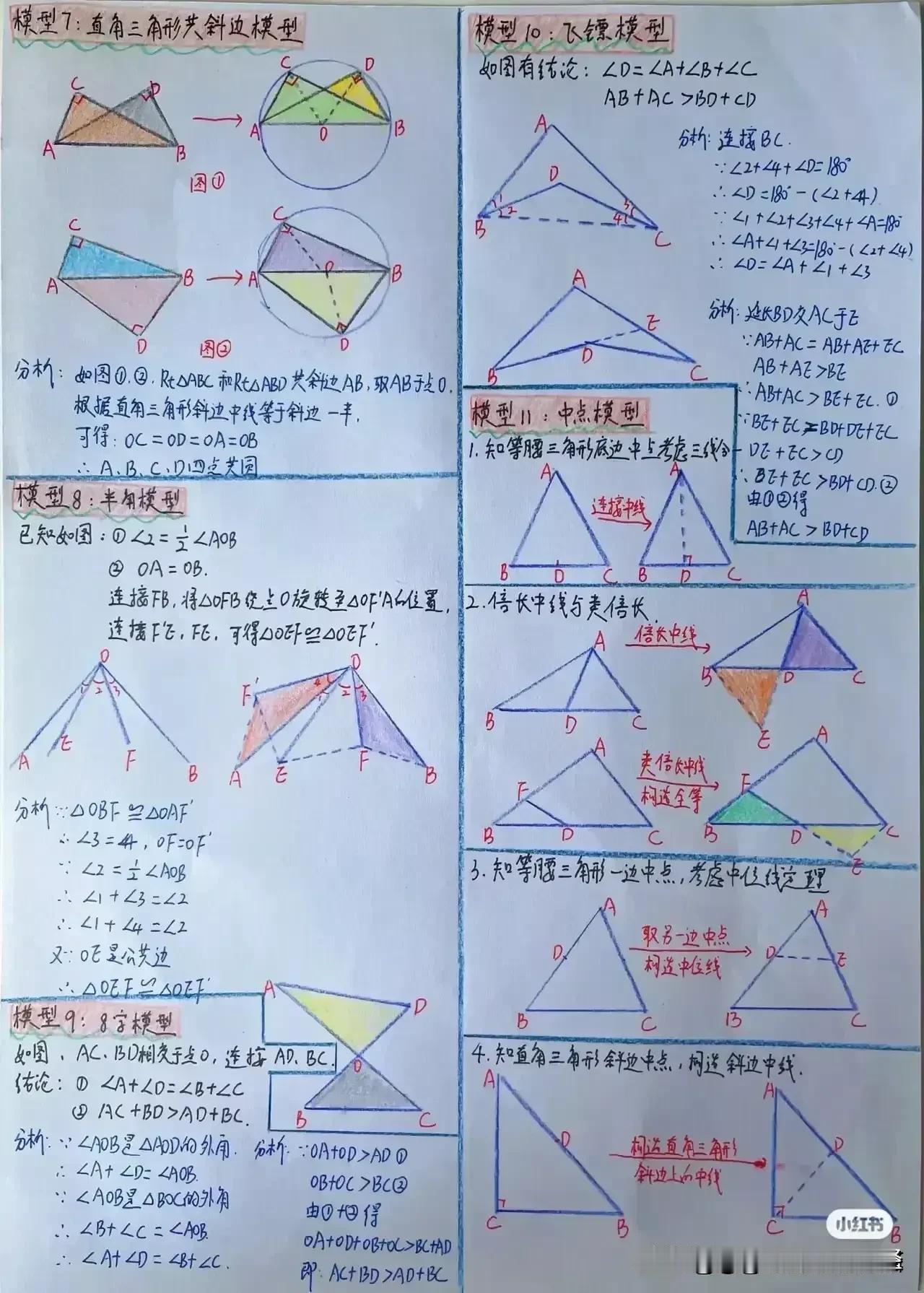
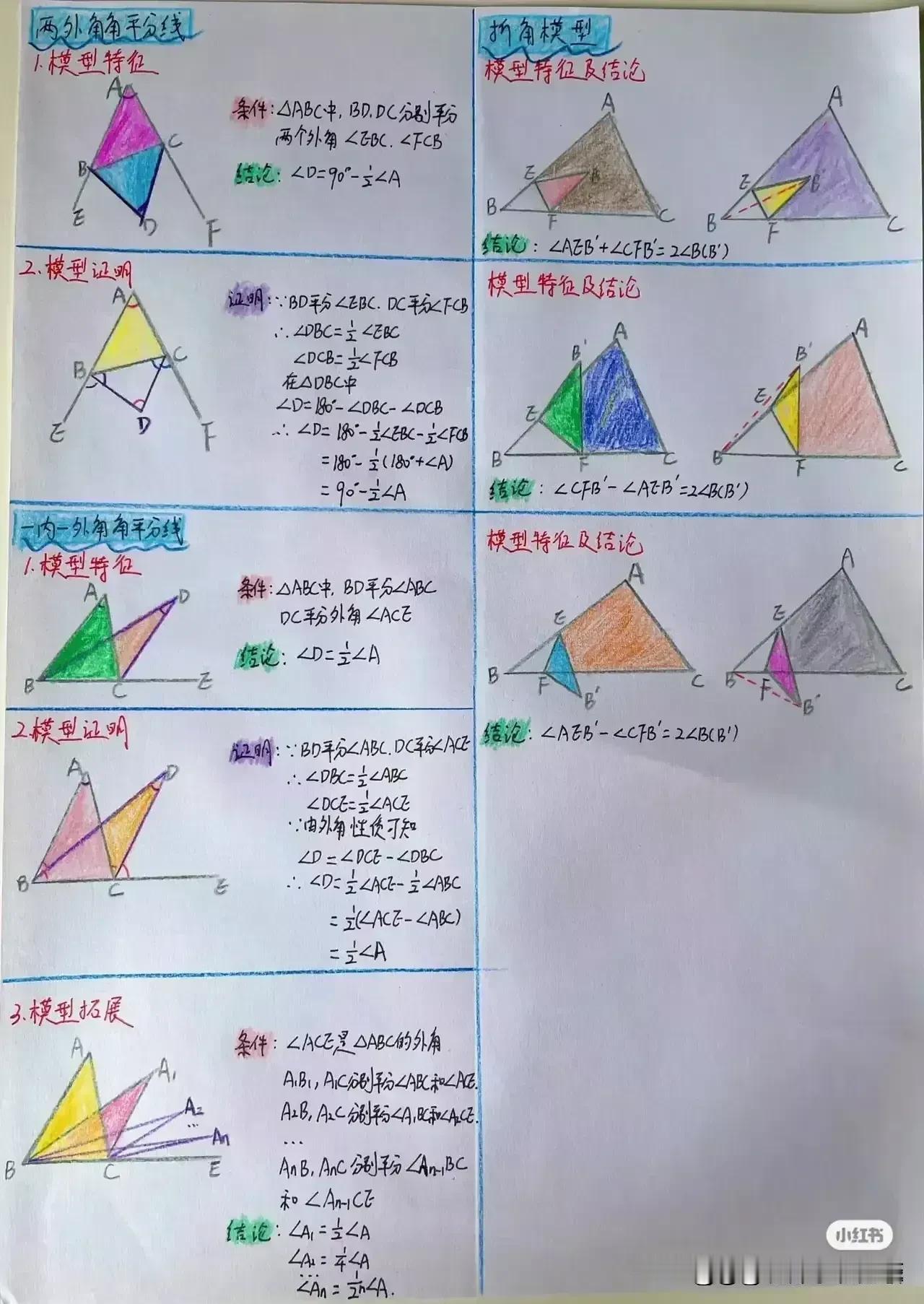
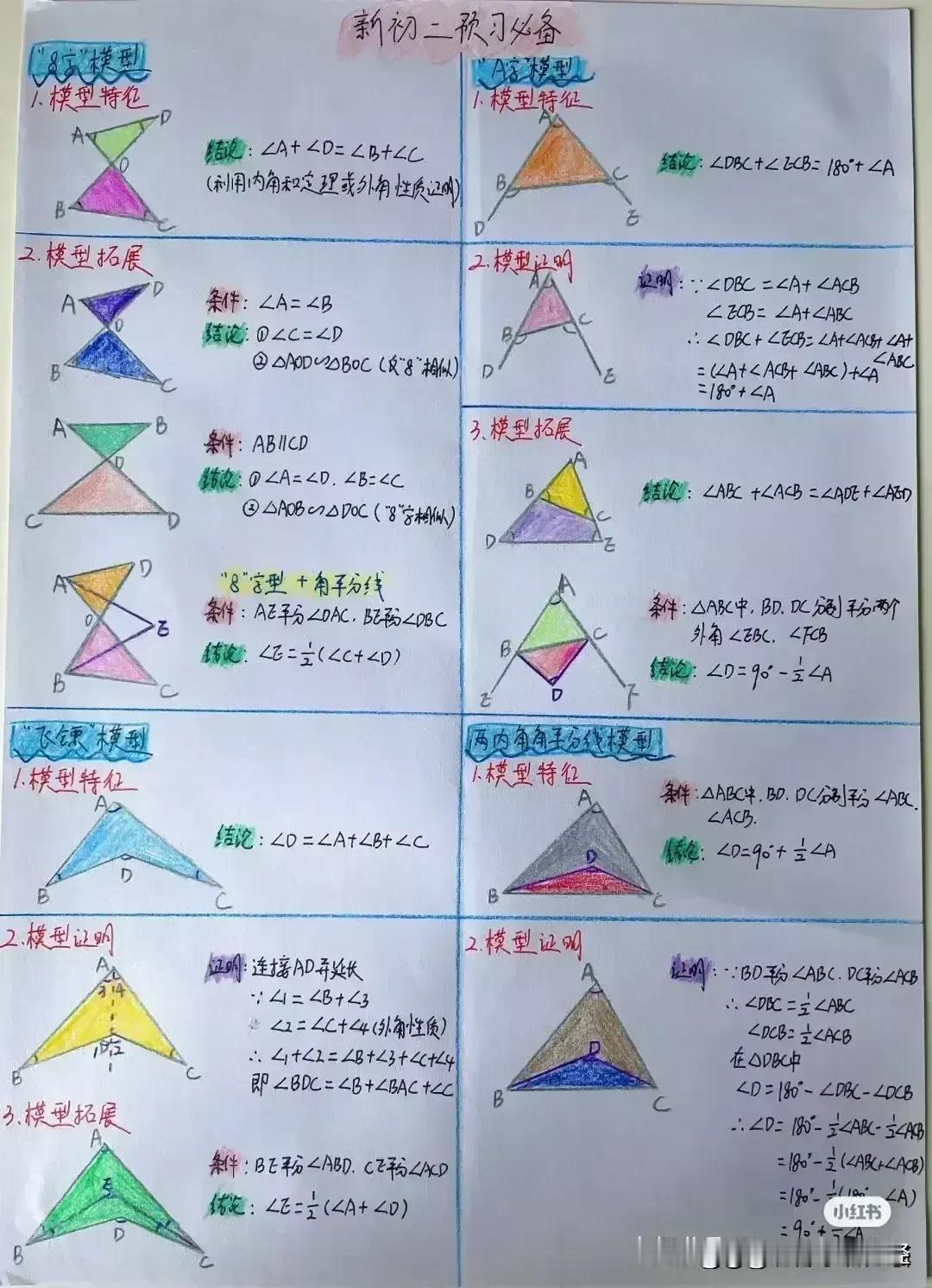
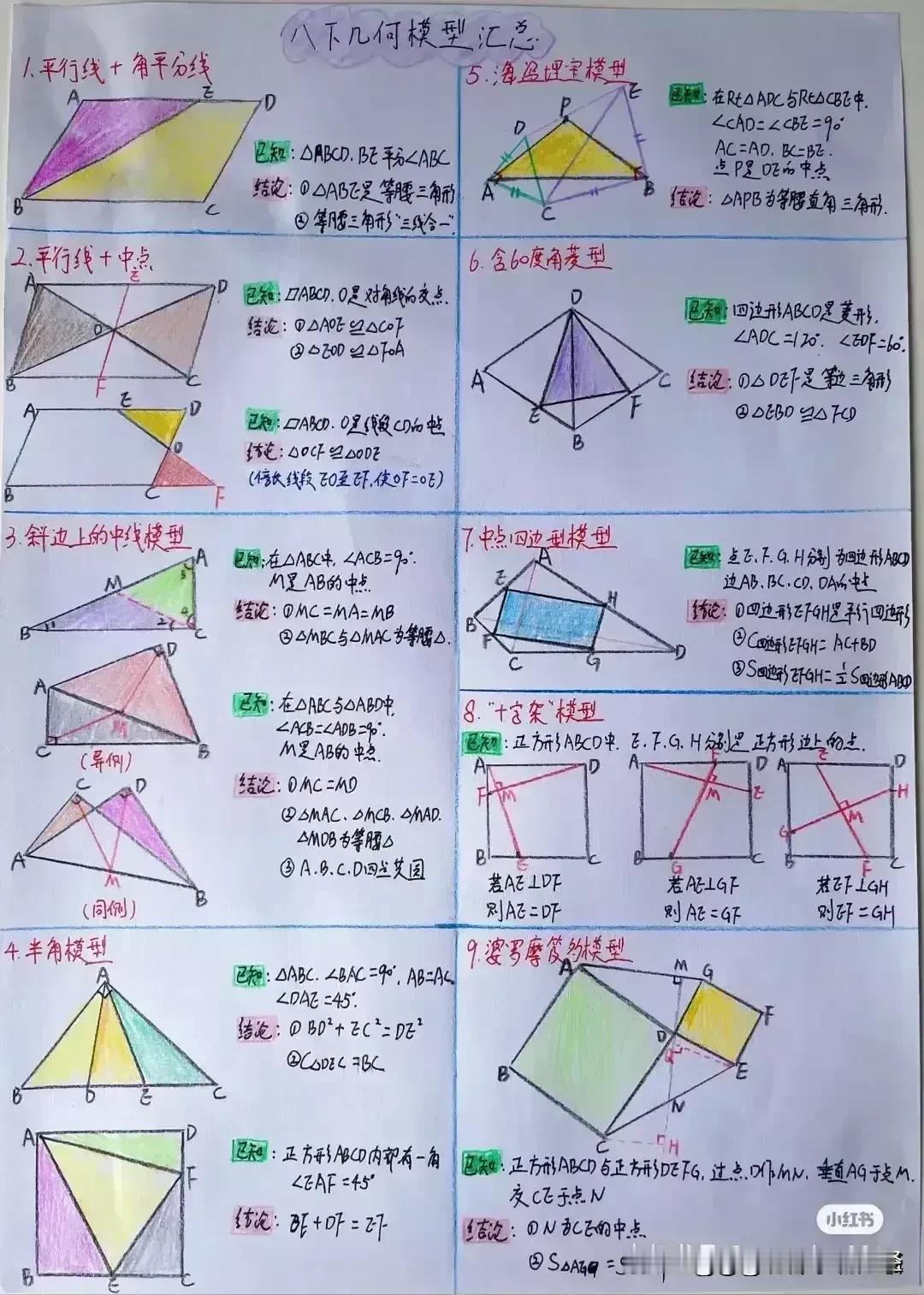
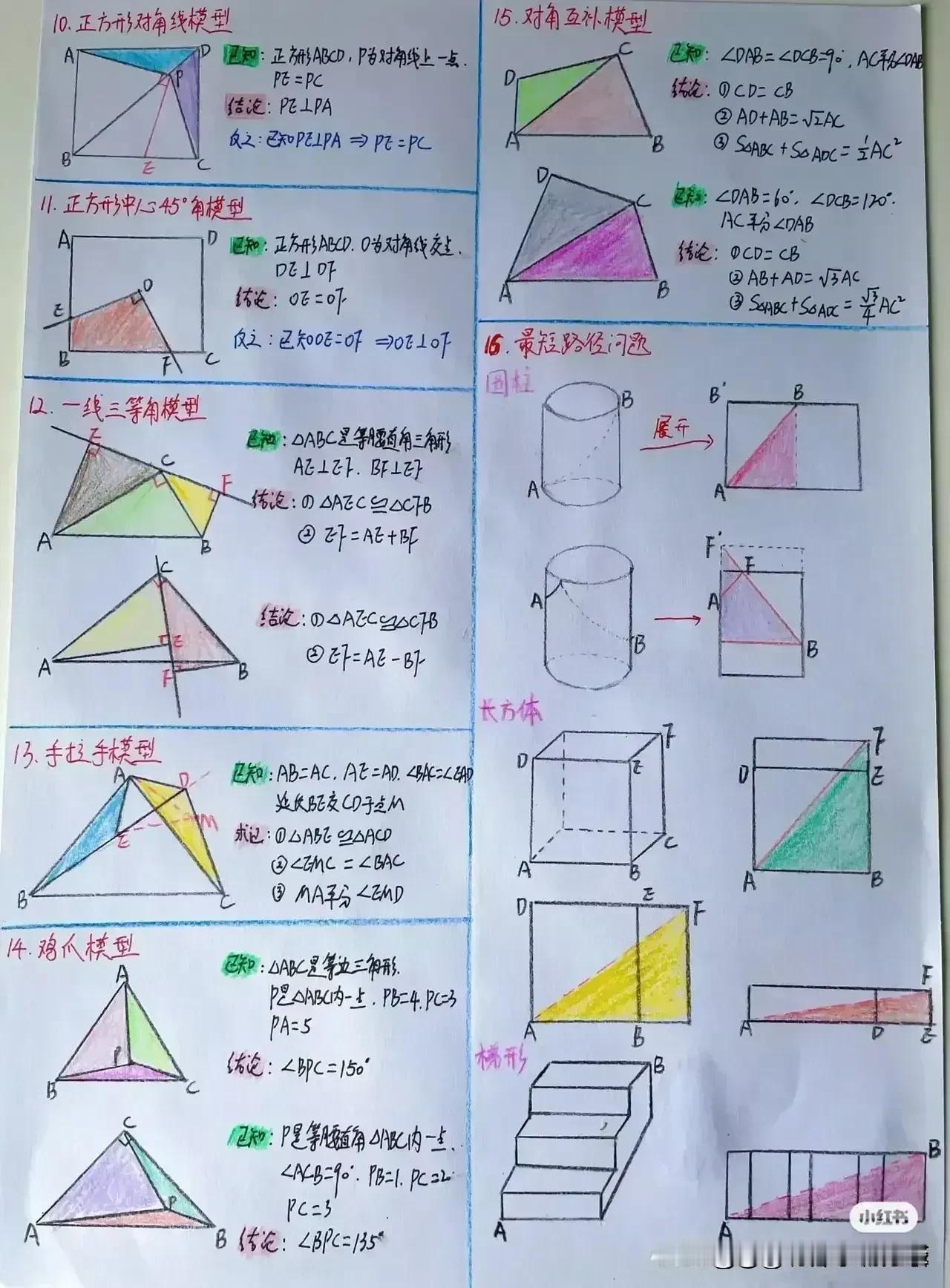
“天哪，太厉害了！”据说一位衡水中学985状元肺腑直言，初中数学几何再难，无非就是这18张纸，孩子再笨，吃透这些初中数学几何模型，也能上110+！包括全等三角形常见模型、相似三角形常见模型、面积相关模型、角平分线常见模型、中点相关模型、线段最值模型、四边形模型以及勾股定理等！没有比衡水中学985状元手写的18张笔记图更专业更系统的整理了！ 全等三角形是初中几何的重要基础，掌握好各种全等三角形模型，对于解决复杂的几何问题至关重要。比如“手拉手”模型，两个等腰三角形，顶角相等，将它们的顶点重合，就像两只手牵在一起一样。通过证明全等，可以得到对应边相等、对应角相等的结论。 例如，在一个等边三角形 ABC 和等边三角形 ADE 中，点 A 为顶点重合点，我们可以通过证明三角形 ABD 和三角形 ACE 全等来解决一系列问题。这种模型在考试中经常出现，只要学生能够准确识别并运用相应的证明方法，就能轻松得分。 相似三角形常见模型同样不容忽视。相似三角形的性质和判定在解决实际问题中有着广泛的应用。比如“一线三等角”模型，一条直线上有三个相等的角，往往可以通过两角对应相等来证明三角形相似。假设在一个图形中，有一条直线上的三个角分别为∠A、∠B、∠C，且∠A = ∠D，∠B = ∠E，那么三角形 ABC 和三角形 DEF 就相似。在解决一些实际测量问题时，我们可以利用相似三角形的对应边成比例来求出未知的长度。 面积相关模型也是初中几何的重要内容之一。比如“等积变换”模型，通过同底等高或等底同高的三角形面积相等的原理，可以进行面积的转化和求解。例如，在一个平行四边形 ABCD 中，连接对角线 AC，三角形 ABC 和三角形 ACD 等底同高，所以它们的面积相等。在求解一些复杂图形的面积时，我们可以利用这种等积变换的方法，将不规则的图形转化为规则的图形进行求解。 角平分线常见模型更是有着独特的作用。角平分线的性质定理和判定定理是解决角平分线相关问题的关键。比如“角平分线+平行线=等腰三角形”模型，当一个角的平分线与一条平行线相交时，所形成的三角形是等腰三角形。例如，在一个三角形 ABC 中，AD 平分∠BAC，且 DE 平行于 AC，那么三角形 ADE 就是等腰三角形。这个模型在证明线段相等和角度相等的问题中非常有用。 中点相关模型也是初中几何的重要考点之一。比如“倍长中线”模型，将三角形的中线延长一倍，构造全等三角形。假设在三角形 ABC 中，D 为 BC 中点，延长 AD 至 E，使 AD = DE，然后连接 BE，就可以证明三角形 ADC 和三角形 EDB 全等。通过这种方法，可以将一些与中点相关的问题转化为全等三角形的问题进行求解。 线段最值模型在初中几何中也经常出现。比如“将军饮马”问题，在一条直线的同侧有两个定点，求在直线上找一点，使得这个点到两个定点的距离之和最小。通过作对称点，利用两点之间线段最短的原理来求解。例如，在直线 l 的同侧有 A、B 两个定点，在直线 l 上找一点 P，使得 PA + PB 最小。我们可以通过作点 A 关于直线 l 的对称点 A'，连接 A'B 与直线 l 的交点就是所求的点 P。 四边形模型包括平行四边形、矩形、菱形、正方形等。这些四边形的性质和判定定理是解决四边形相关问题的基础。比如平行四边形的对边平行且相等、对角相等、对角线互相平分等性质。在证明一个四边形是平行四边形时，可以根据不同的条件选择相应的判定方法。例如，一组对边平行且相等的四边形是平行四边形；两组对边分别平行的四边形是平行四边形等。 勾股定理更是初中几何的经典内容。在直角三角形中，两条直角边的平方和等于斜边的平方。这个定理在解决直角三角形的边长问题、求线段长度、证明几何关系等方面有着广泛的应用。例如，在一个直角三角形 ABC 中，∠C = 90°，已知直角边 AC = 3，BC = 4，根据勾股定理可以求出斜边 AB 的长度为 5。 衡水中学的这位 985 状元，通过自己的努力和总结，将初中数学几何的核心内容浓缩在这 18 张纸上，这些笔记图不仅专业而且系统，涵盖了初中数学几何的各个方面。对于学生来说，只要认真钻研这 18 张纸，理解每个模型的原理和应用方法，结合大量的练习题进行巩固，就一定能够在初中数学几何的学习中取得突破。 所以那些家里有孩子的，家长工作再忙也要抽出时间来保存收藏给孩子看一看，学一学，记一记，背一背这些几何模型解题思路，不过光说不练假把式，如果孩子基础实在薄弱，更多衡水学霸笔记下方链接走起！ 衡水中学状元手写笔记