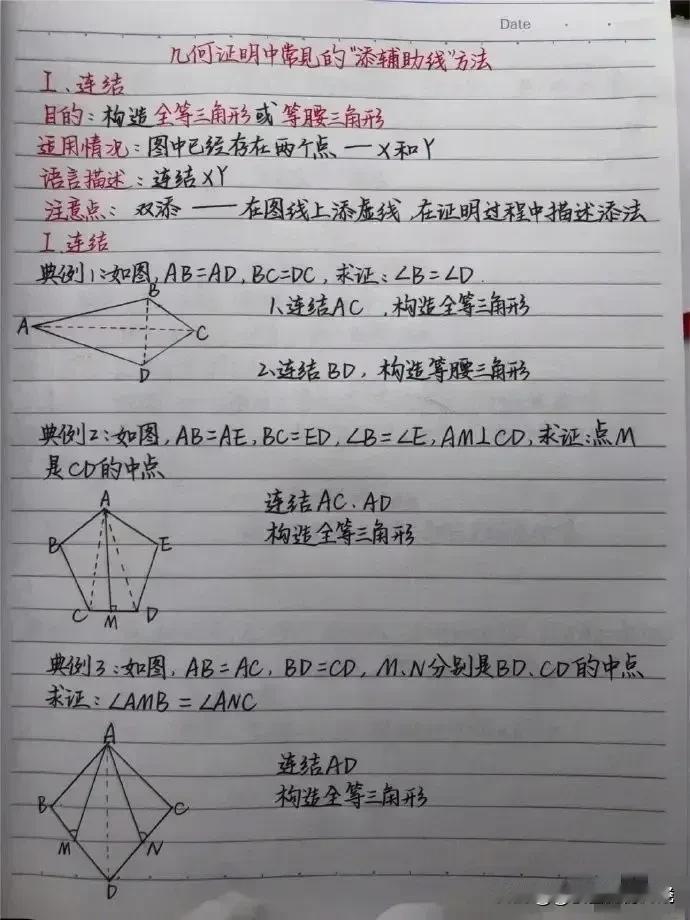
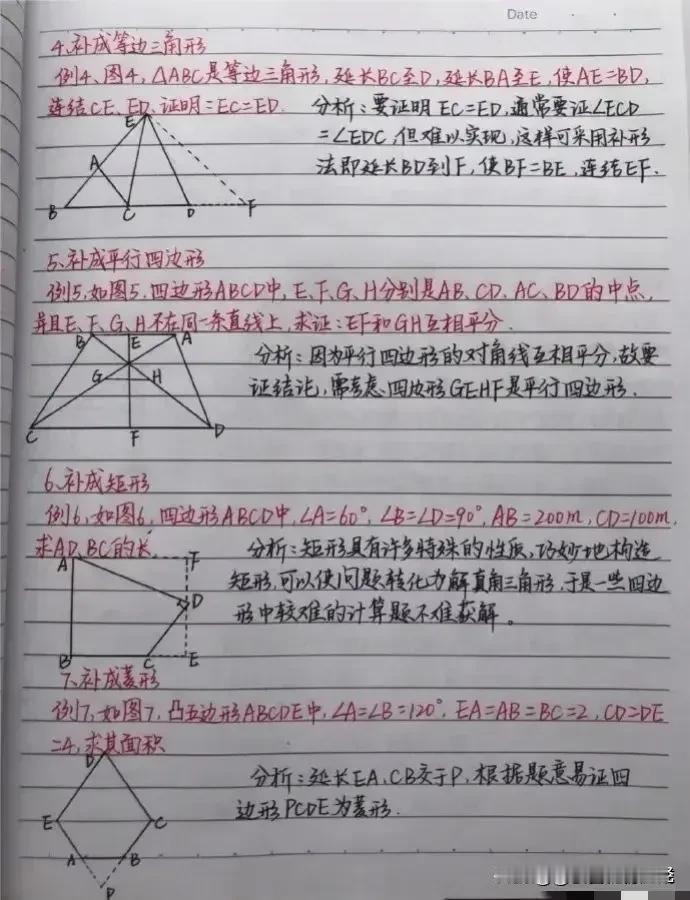
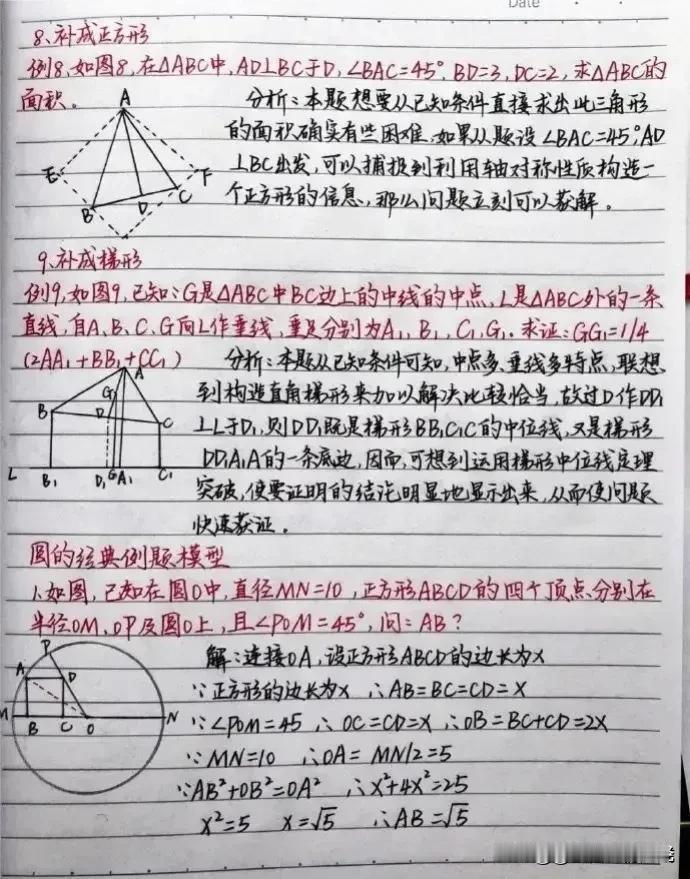
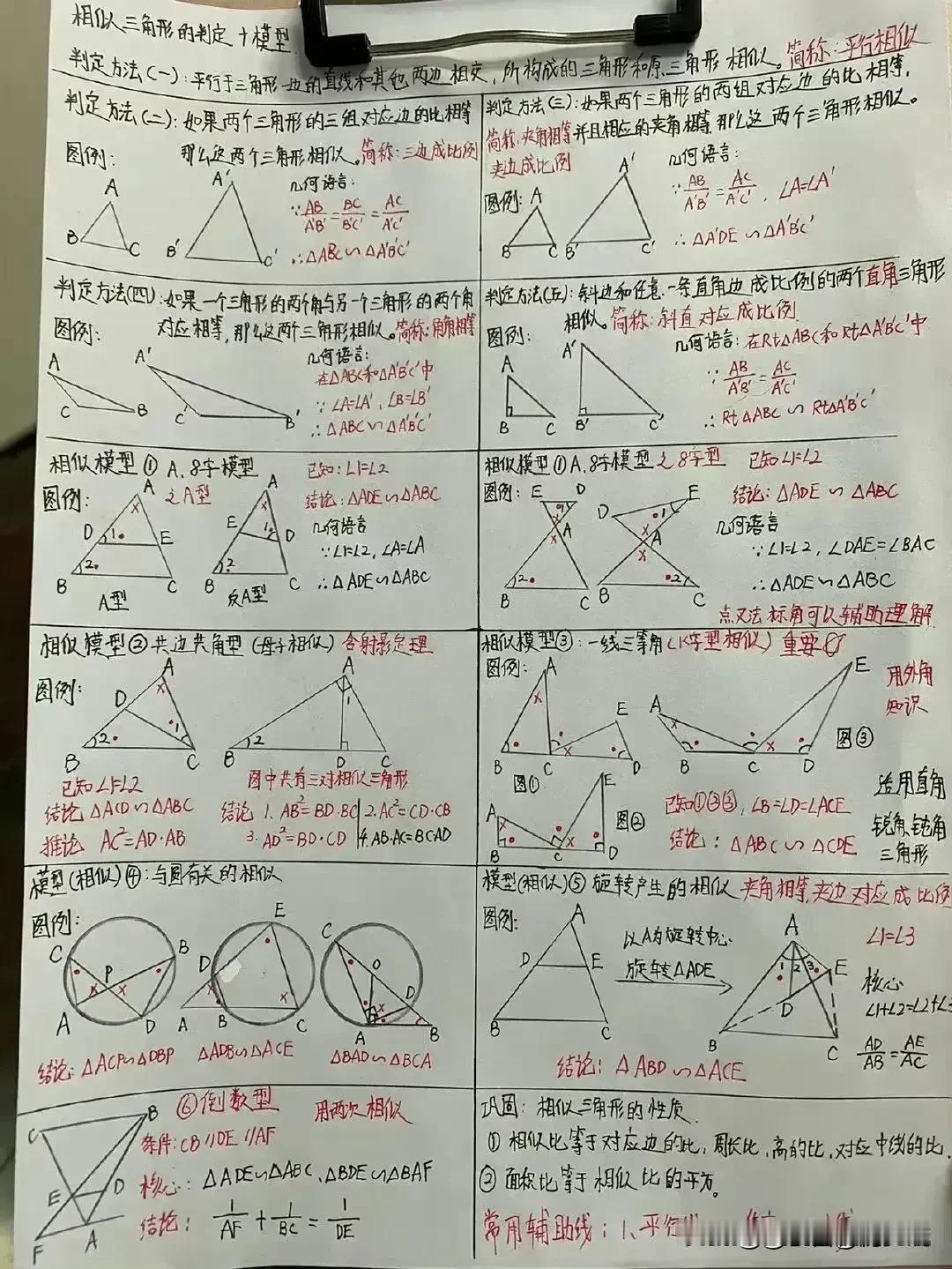
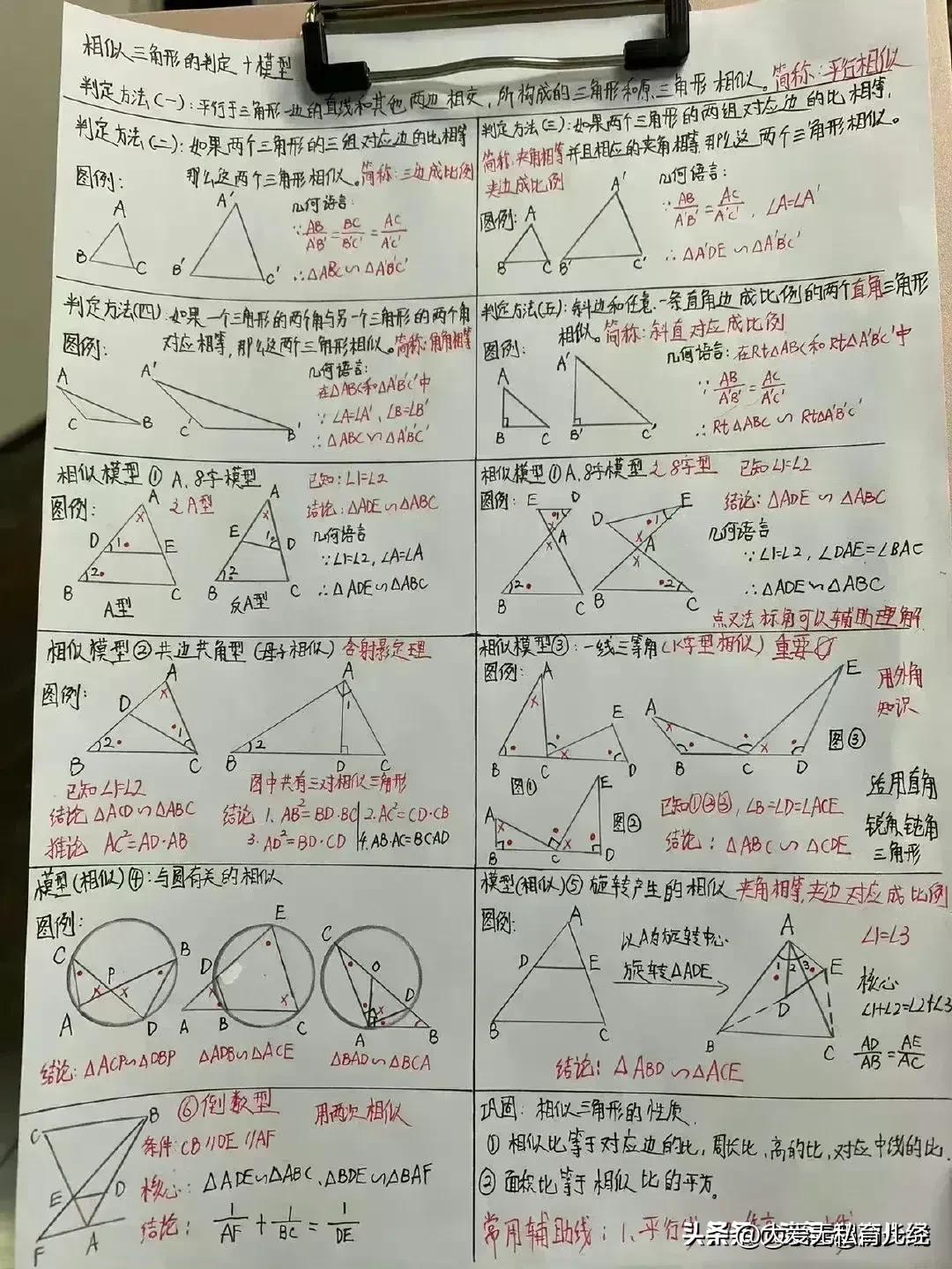
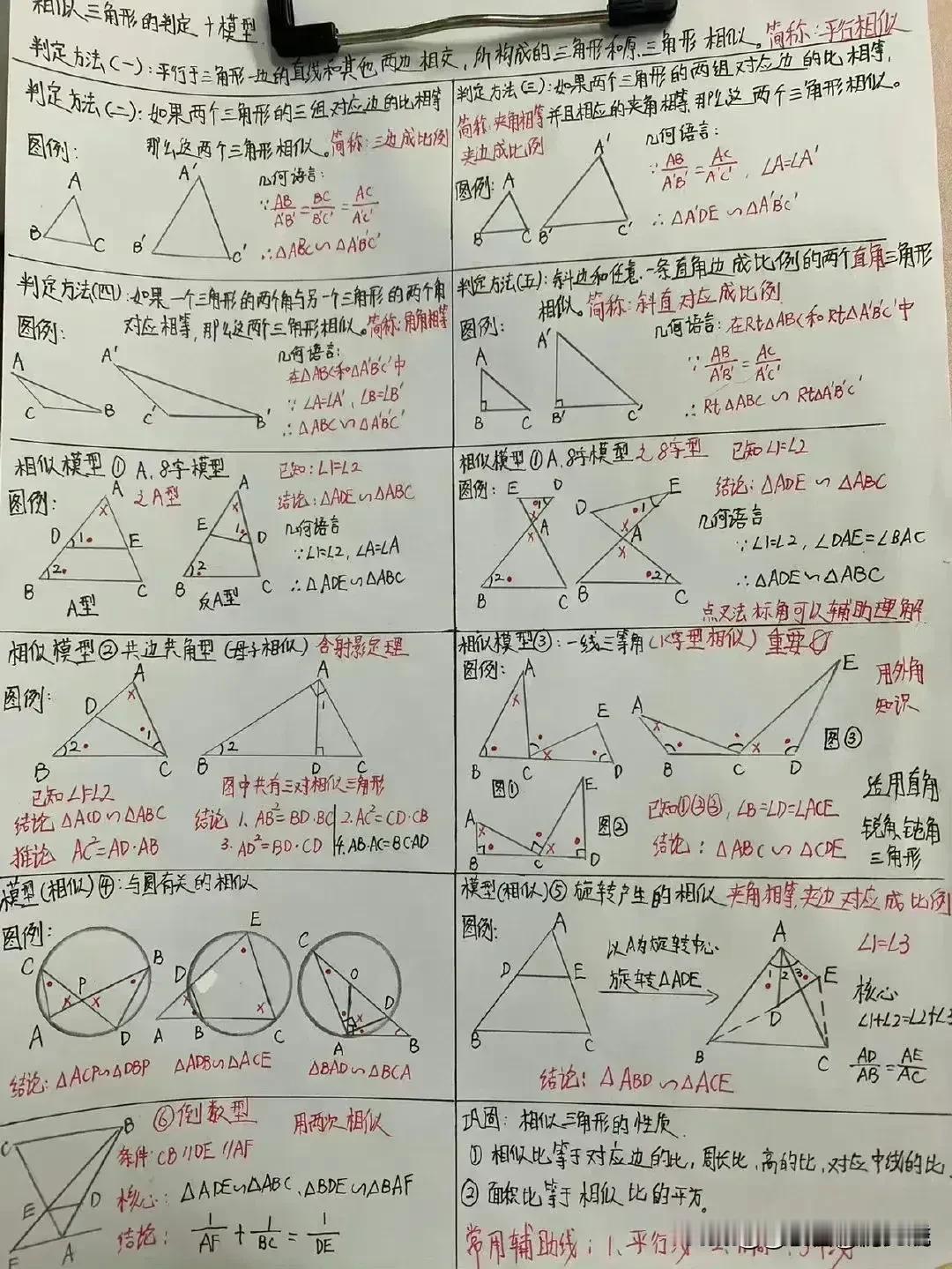
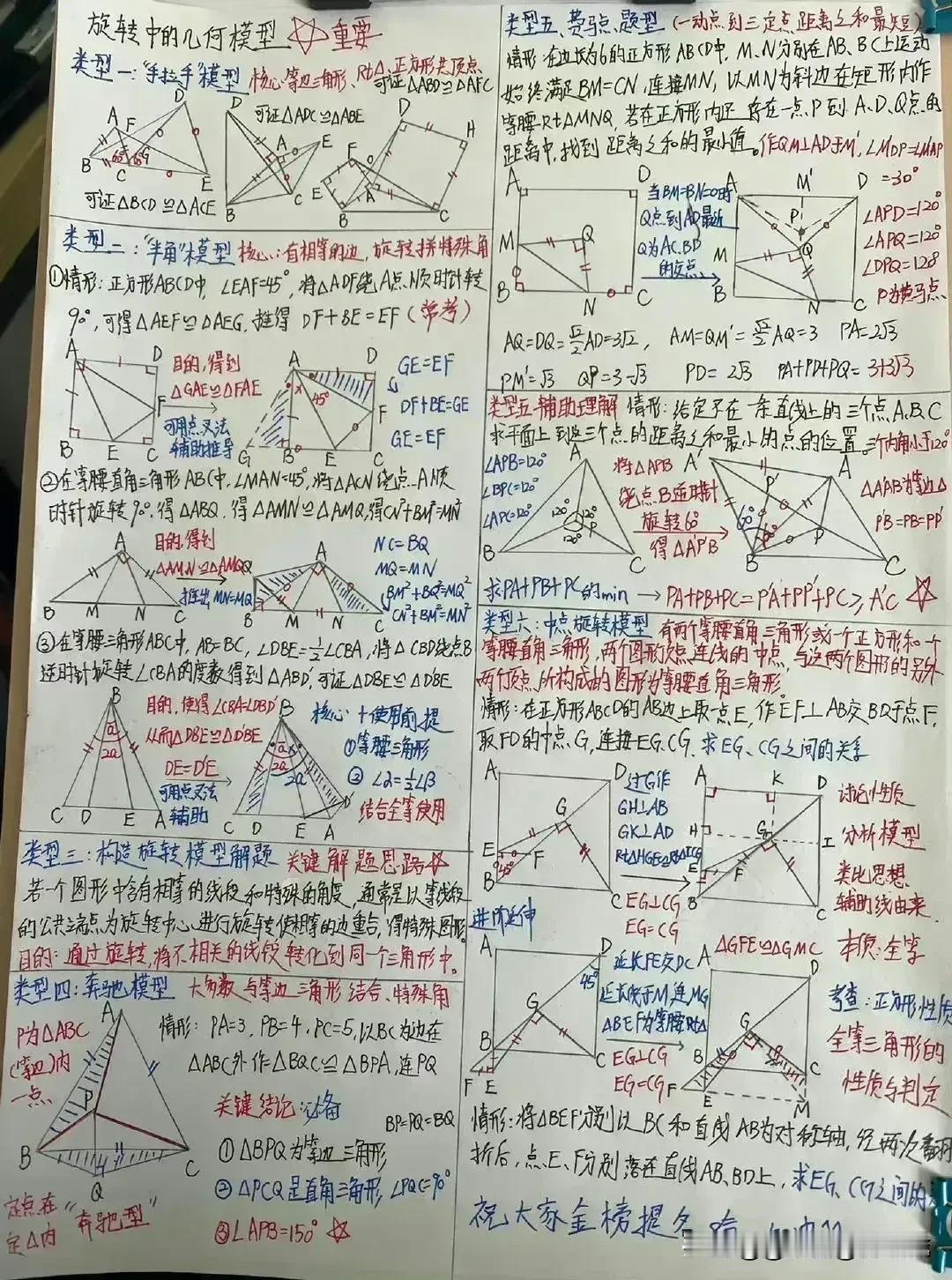
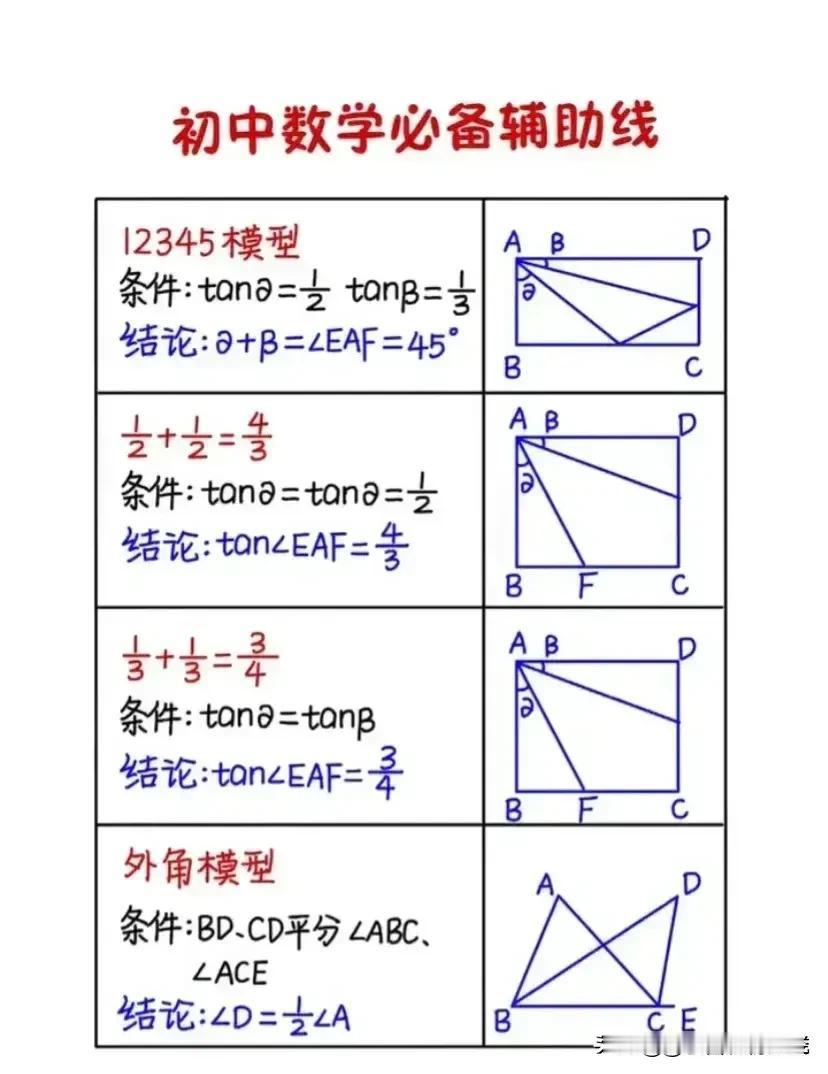
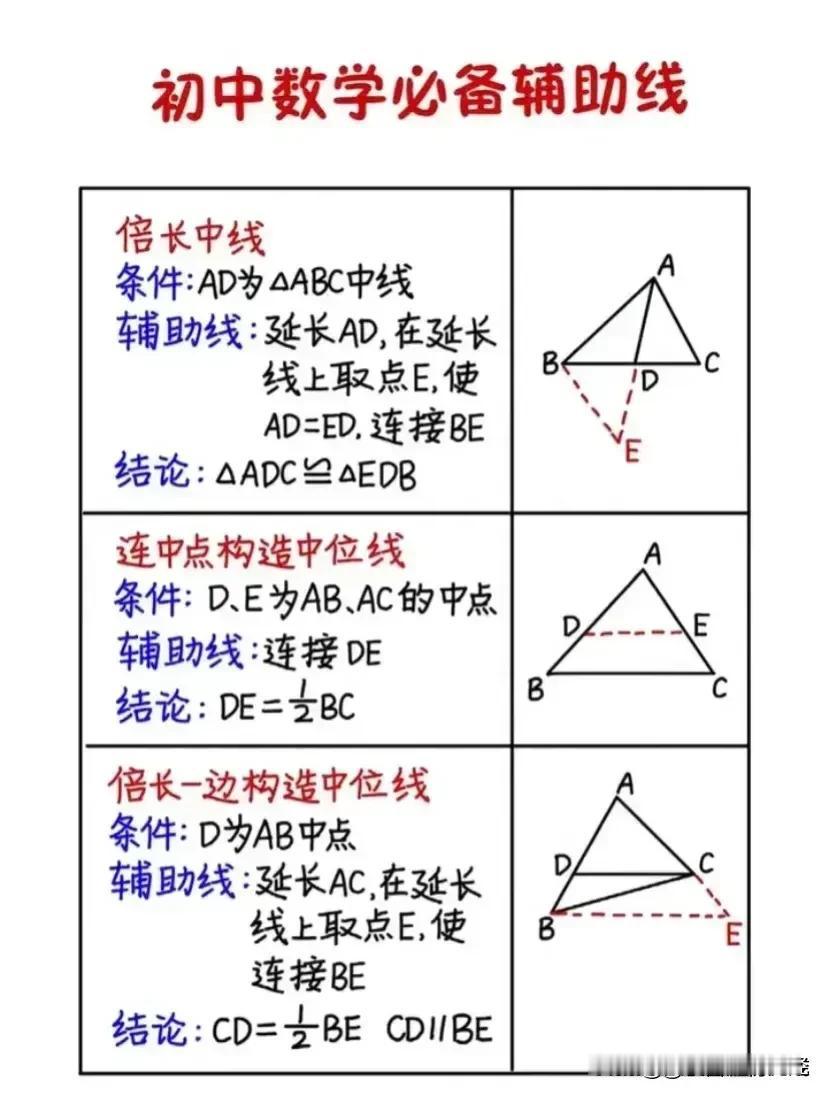
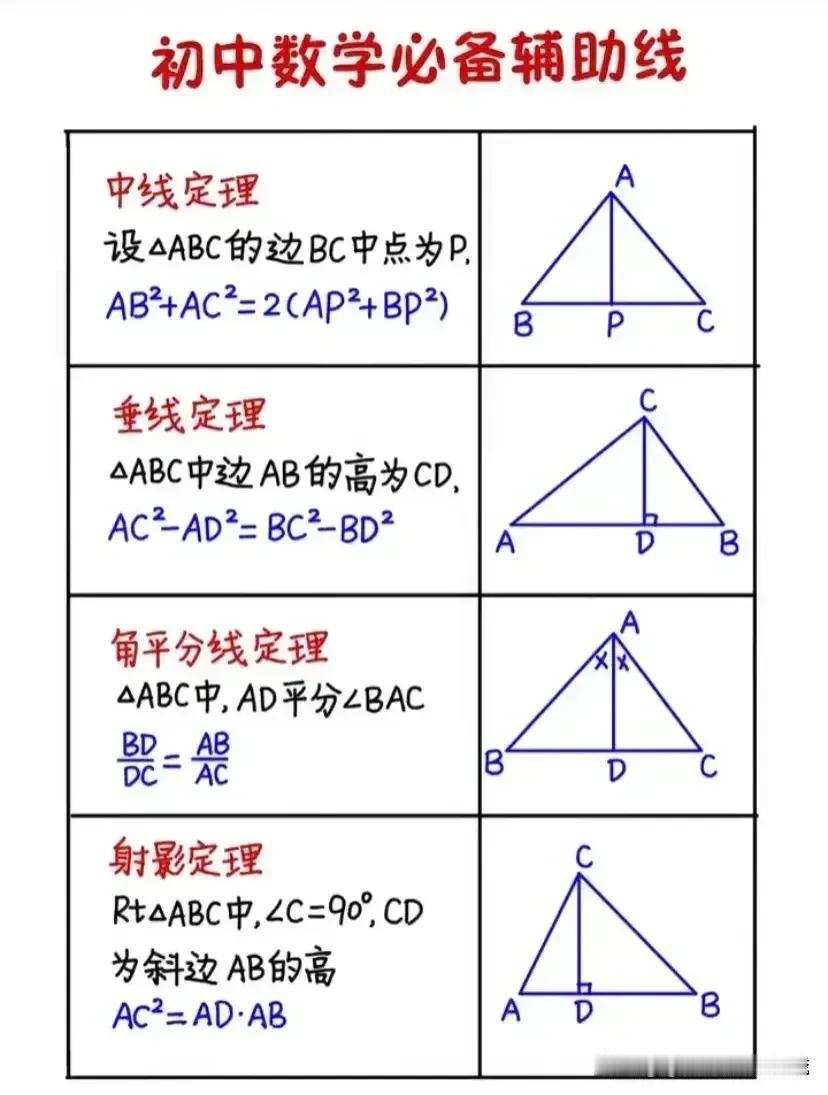
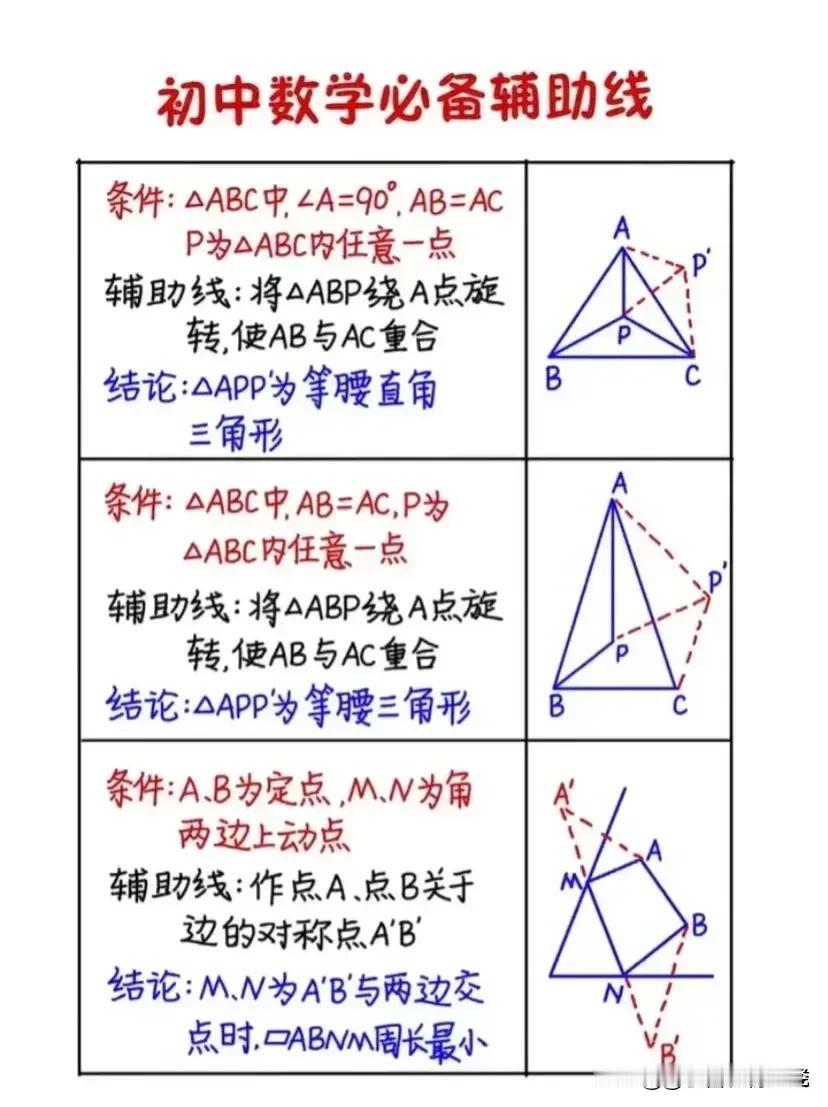
“我滴天呐，太厉害了！”据说一位70岁退休数学老师，为了帮孙子提高数学成绩，一口气把初中数学14条必备辅助线和常见添加辅助线的方法手写出来了，并附带详细解题思路和结论，太适合零基础的孩子查漏补缺巩固基础！ 这些辅助线包括但不限于：垂直平分线、角平分线、中线、高线、平行线、过一点作直线的垂线、构造等腰三角形或等边三角形、利用圆的性质作半径或弦心距等。每一条辅助线的引入，都伴随着老师精心设计的解题思路，确保学生不仅知其然，更知其所以然。 1. 垂直平分线 在解决线段相等或角相等的问题时，垂直平分线往往能发挥奇效。例如，在证明三角形两边之和大于第三边的题目中，通过作一边的垂直平分线，可以巧妙地构造出两个直角三角形，利用勾股定理或直角三角形的性质，轻松得出结论。 2. 角平分线 角平分线在处理角度问题时尤为关键。比如，在证明两个角相等时，若能直接或通过构造作出这两个角的平分线，往往能利用“角平分线+平行线=等腰三角形”的性质，简化证明过程。一个典型的例子是，在等腰三角形中，通过作顶角的平分线，可以快速证明底边上的两个底角相等。 3. 中线 中线在三角形中扮演着连接两端、平衡全局的角色。它不仅能将对边平分，还能与对应的底边构成平行关系，为解题提供便利。例如，在解决三角形面积问题时，利用中线将三角形分割成两个面积相等的小三角形，可以简化计算。 4. 高线 高线是连接顶点与对边（或其延长线）的垂线段，它在计算三角形面积、判断三角形形状等方面有着重要作用。特别是在直角三角形中，高线往往与直角边重合，为解题提供了直观的依据。 5. 构造特殊三角形 在某些复杂问题中，通过构造等腰三角形、等边三角形或直角三角形等特殊图形，可以利用这些图形的特有性质，简化问题。例如，在证明两条线段相等时，若能在图形中构造出一个等腰三角形，那么这两条线段很可能就是等腰三角形的两腰，从而得证。 对于每一种辅助线的应用，老师都附上了详尽的解题思路和结论，确保即使是零基础的孩子也能跟上节奏，逐步掌握。他强调，添加辅助线并非盲目之举，而是基于对题目条件的深入分析和对数学定理的熟练掌握。在解题过程中，老师鼓励学生多尝试、多思考，从不同角度审视问题，寻找最佳的辅助线添加方案。 此外，老师还特别提到了辅助线在培养数学思维方面的重要作用。通过不断练习，学生可以逐渐学会如何抽象地思考问题，如何将复杂的数学问题转化为直观的几何图形，进而提高解决问题的能力。 家有孩子的，家长再忙也要收藏起来给孩子看一看学一学记一记背一背这些辅助线模型，对于孩子学好数学有很大的帮助，能提高不少分。如果孩子数学基础实在薄弱，可以获取更多更详细的更全面的初中数学几何辅助线可以下方链接走起！ 中考几何辅助线