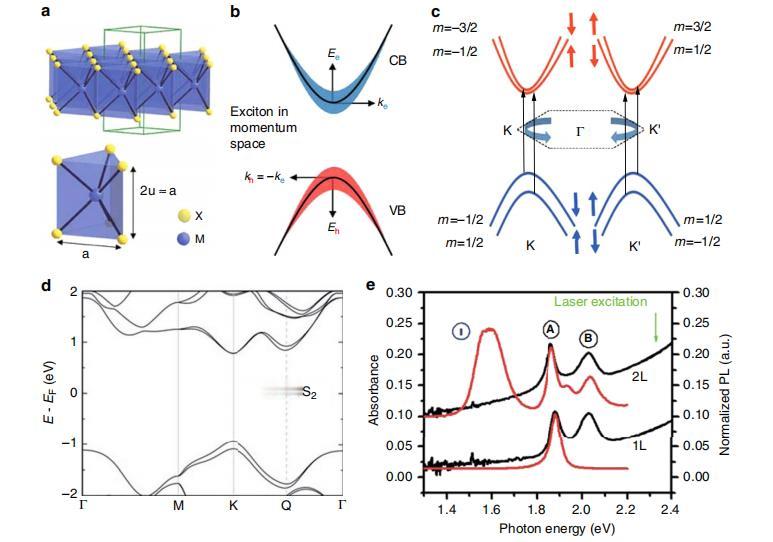
从应变场到带结构调谐，非Bravais晶格和石墨烯经历了怎样的应变   前言：石墨烯的发现标志着二维(2D)材料领域的一个重要里程碑，它是通过一种被称为从大块石墨中机械剥离的过程出现的，这为研究人员提供了一个探索各种2D材料的切入点，这些材料以其层状结构为特征，在其平面内具有强共价键，而层间范德华相互作用相对较弱，这种独特的成分赋予它们独特的电子结构和非凡的物理化学性质。   作为2D的先驱材料，石墨烯展现出了耐人寻味的特性，但它的电荷载流子表现出无质量的狄拉克费米子行为，类似于以接近“光速”的速度穿越的相对论粒子这种现象在布里渊区内的无隙K点和K’点附近最为明显。   然而，原始石墨烯确实有局限性，它缺乏固有的光学带隙，因此，它在发光环境中的应用受到一定的限制，具有零带隙特性的材料在连续波激发下通常不会发光，除非在某些情况下，如变形的2D材料。   从宏观的角度来看，变形的2D材料在外加应变下的行为可以用连续弹性理论来有效地描述，当变形的长度尺度远大于材料的晶格常数时，这种方法是适用的，储存在2D材料中的弹性能量可以分为两个部分，拉伸能量和弯曲能量。   在这种情况下，设想一个2D材料的变形晶体结构中的普通原子，最初位于坐标r = (x，y)，作为变形的结果，对于面内变形，原子经历由矢量场u(r) = (ux(r)，uy(r))表示的位移，对于面外变形，原子经历由矢量场h(r)表示的位移，应变是二阶张量场，用εij表示，并使用以下表达式计算:εij = 1/2 * (∂iuj + ∂jui + ∂ih∂jh)。   其中I，j ∈ {x，y}，各向异性膜的弹性能量密度Fel(对哈密尔顿函数的势能起作用的因素)可以分为拉伸能量密度Fst(与平面内相对距离的变化相关)和弯曲能量密度Fb(由平面构型的偏差产生)，这些量表示为:Fel = Fst + Fb，用Fst = 1/2 * λεii^2 + 2μεijεij和Fb = 1/2 * κ * (∇^2h)^2，其中λ和μ代表材料的平面内Lamé常数，κ代表弯曲刚度。   拉伸能量密度Fst可以明确表示如下:FST = y2d/2 *(1-ν^2)*(εxx^2+εyy^2+2ν*εxx *εYY+1/ν* εxy^2)，其中，Y2d和ν分别表示2d杨氏模量和泊松比，这些参数可以用Lamé常数表示如下:Y2d = λ + 2μ * (1 - ν^2)，ν = λ / (λ + 2μ)。   考虑到拉伸和弯曲能量之间的相互作用以及材料的固有属性，如杨氏模量、泊松比和拉梅常数，这一综合框架能够描述和理解变形2D材料的力学行为。   一个重要的观察结果是，拉梅常数和弯曲刚度可以通过价力场与2D材料的微观参数联系起来，通过建立这种联系，方程提供了一种在宏观应变和这些材料的微观特征之间建立联系的方法，事实证明，这个桥接框架对于理解外力和材料内在属性之间的相互作用至关重要。   应用这些方程可以深入了解电子能带结构，这是通过使用紧束缚(TB)和k⋅p模型构建微观哈密顿量来实现的，该模型由在给定应变下最小化弹性能(Fel)获得的应变-位移关系来提供信息，从而确保机械平衡。   为了进一步说明，对于具有非Bravais晶格的应变材料，应变相关的第一近邻矢量δ0_n采用I + ε * δn的形式，其中ε表示应变张量，位移u(r)通过u(r) = ε r与应变相关，然而，在处理这种晶格配置时，这种简化在柯西-玻恩近似下失效，需要进行修正：δ0 _ n = I+ε*δn+δ。   这里，附加位移项δ考虑了由原始晶胞中的多个基本原子引入的附加自由度，矢量δ的确定包括最小化材料的变形能，通过引入这种精确的理解，考虑了第一近邻矢量的紧束缚(TB)哈密顿量可以用来分析应变对石墨烯晶格的影响，这种方法为研究应变对这些材料的电子性质及其晶格结构的影响铺平了道路。   尤其是过渡金属二硫族化物(TMDCs)和石墨烯，主要目的是阐明如何有策略地应用应变来定制和控制这些材料的独特光学特性，审查包括不同的方面，从弹性理论和有效的低能哈密顿的彻底探索开始，这些理论基础是理解2D材料在受到宏观和微观应变时表现出的物理性质的复杂相互作用的无价工具。   总结：通过将理论和实验联系起来，对石墨烯等D材料进行了全面的分析，展示了应变如何能够作为强有力的工具来重塑这些材料的电子能带结构，这种操作导致了意想不到的光学性质的出现。   而且除了理论性的论述之外，实验还通过总结产生不同类型菌株的各种技术来深入实践领域，这些技术不仅在他们自己的权利上被讨论，而且在光子学的领域内被连接到他们的相应的应用，这有助于强调操纵应变在各种光子研究中的潜在实用价值。