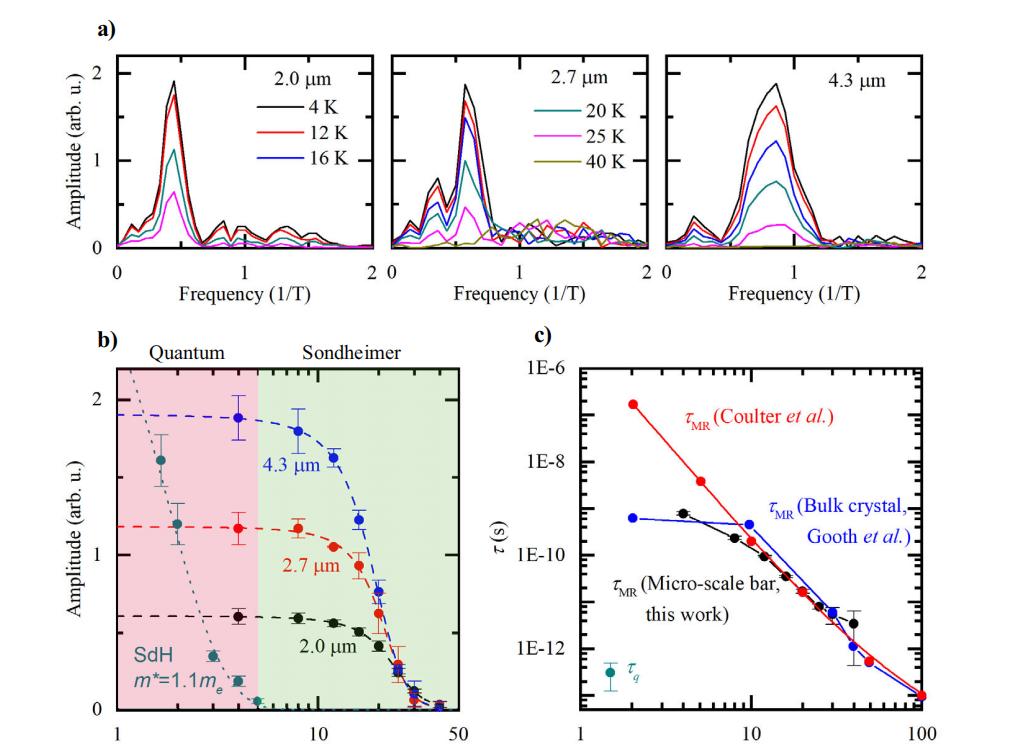
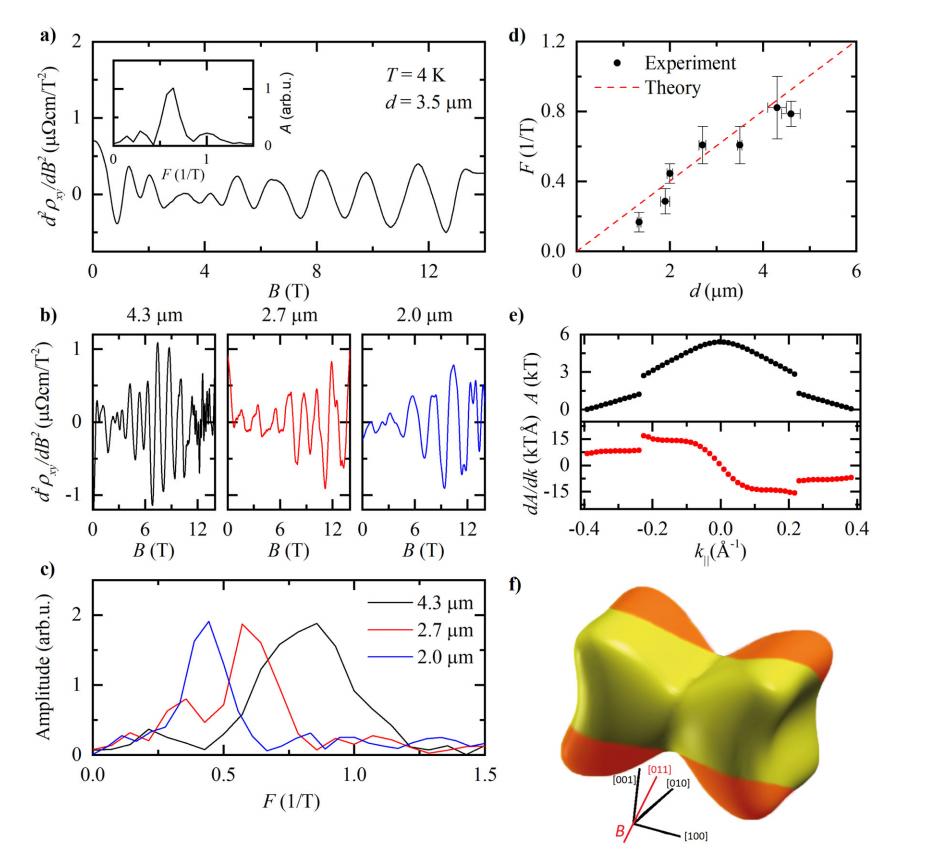
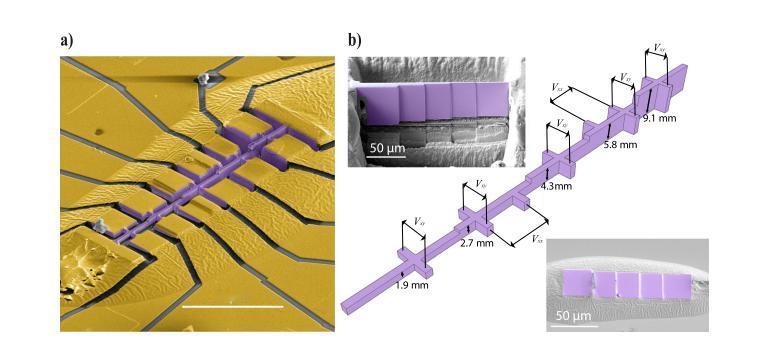
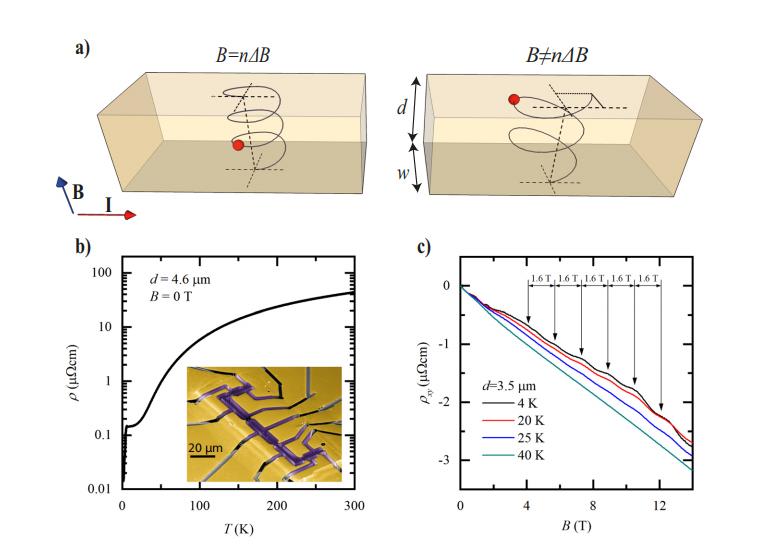
自旋轨道(SO)中的量子振荡(∂A/∂k = 0)在费米能级(Ef)下的扩散行为   前言：在宏观金属线中，采用“体”电导率的概念，假设电荷载流子的运动在微观水平上经历频繁的散射事件，其特征在于平均自由程显著小于导线的尺寸(表示为d)，这导致电流的扩散行为。   然而，当观察微观导体时，会出现不同的情况，其中影响电阻的主要因素是边界散射，这掩盖了体内的内部散射过程，使电阻测量变得复杂，对于微尺度金属，这不仅是量子电子器件发展的组成部分，也是理解微小电流模式的必要条件，一种新的方法被引入来揭示隐藏的体散射过程。   由于它潜在的技术含义及其对增强我们对微观环境中电流的基本理解的贡献，这种方法具有重要意义，所以在传导电子领域，这些电子的行为受到它们对∂k/∂A的依赖性的影响。   当与尺寸为d的结构相互作用时，导致不同的可公度场，这种复杂的相互作用对总电导率产生振荡贡献，然而，这些振荡往往会减弱，除非相当多的状态在费米能级(Ef)下共享相同的vk/∂k∂A值。   在深入研究费米表面的费米学的早期阶段，科学家利用几何近似来描述费米表面，这些近似法通常涉及椭圆端点，是一种识别广义几何属性的方法，这些属性会导致∂k/∂A.常数范围的扩大，不过，随着现代计算方法的出现，已经采用了一种更复杂的方法，当代技术，如从头计算方法，能够通过数值切片计算费米表面，该程序包括确定这些表面的横截面积A(k∨)。   鉴于这些进展，提出了一项建议，以扩大表面切片的常规做法，这是通常用来确定与量子振荡(∂A/∂k = 0)有关的极端轨道，这个提议包括利用费米表面切片代码SKEAF，如方法部分所详述，这样做的目的是识别费米表面上对自旋轨道相互作用特别敏感的区域(∂^2A/∂k^2 = 0)，这种技术的扩展有可能揭示自旋轨道相互作用影响显著的领域，进一步增强我们对这些复杂现象的理解。   自旋轨道相互作用(SO)是由于电荷载流子在真实空间中的运动而产生的，因此对导体的形状施加了某些条件，首先，表面散射需要主要表现出扩散行为，当电子在经历扩散散射之前经历多次镜面散射时，每一次这样的出现都会产生这样的效果，就好像导体具有对应于镜面散射事件数量(N)的有效厚度一样，这实际上会导致泛音的产生。   可是在完美镜面边界条件的理想化场景中，SO效应消失，这是因为这样的边界条件，作为动力学的镜子，消除了电子系统和导体的有限尺寸之间的任何相互作用。   其次，导体必须满足特定的几何标准，它应该有两个垂直于磁场的平行平面，这种几何形状确保在整个导体上只选择一个螺旋轨迹。   平行性的要求来自于特定磁场下螺旋轨迹的一部分间距，该分数由最大厚度变化(δd)除以电子速度(vk)和弛豫时间(τc)的乘积给出，即δd < vkτc = dδB/B，这些条件在平面电子器件中自然得到满足，因为这些器件固有地呈现平行的平面表面，并且有助于SO效应的必要几何先决条件。   实质上，导体中自旋轨道相互作用(SO)出现的必要条件，与真实空间中电荷载流子的行为和导体的形状密切相关，研究强调了主要的表面漫射散射的重要性，镜面散射事件的影响，以及平行平面表面的几何要求，并且这些条件通常在平面电子器件中得到满足，使它们成为观察SO效应的合适平台。   而自旋轨道(SO)效应的可观测性取决于一个关键条件，就是电子在导体的平行表面之间穿行时，不会遇到大角度散射事件，为了满足这一要求，动量弛豫导致的电子平均自由程(lMR)必须大于表面之间的距离(d)，因此lMR > d，lMR(T)的温度依赖性起着关键作用，lMR随温度升高而降低。   相反，假设边界散射与温度无关，s0幅度的抑制由关系式e^(-d/lMR(T决定，其中lMR(T)的减小导致幅度的相应减小，这种抑制允许在有限大小的样本内估计体输运平均自由程，即使当样本的尺寸(d)远小于平均自由程(lMR)时，利用1 / lMR(T) = 1 / d * ln[A(T) / A(0)]这个表达式依旧可以实现。   总结：通过这次研究，强调了自旋轨道效应可观测性的关键条件，即平行表面之间不存在大角度散射事件，它讨论了平均自由程(lMR)的温度相关行为及其与表面间距离(d)的关系，不仅如此，它还介绍了so振幅抑制的概念及其与有限尺寸样品中体输运平均自由程的关系，使用外推法估计A(T = 0)类似于在低温下大块金属电阻率中观察到的类似行为。