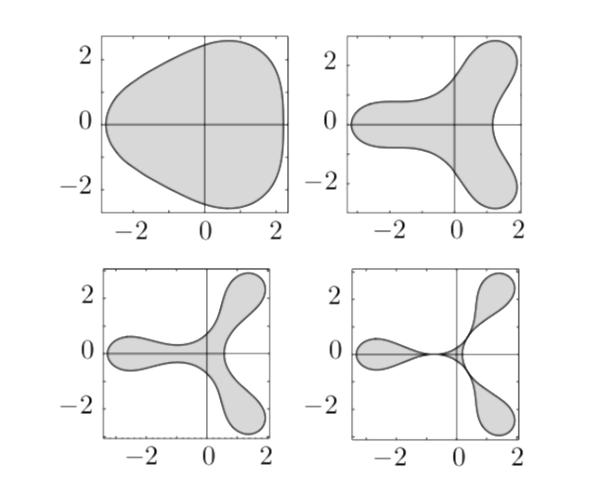
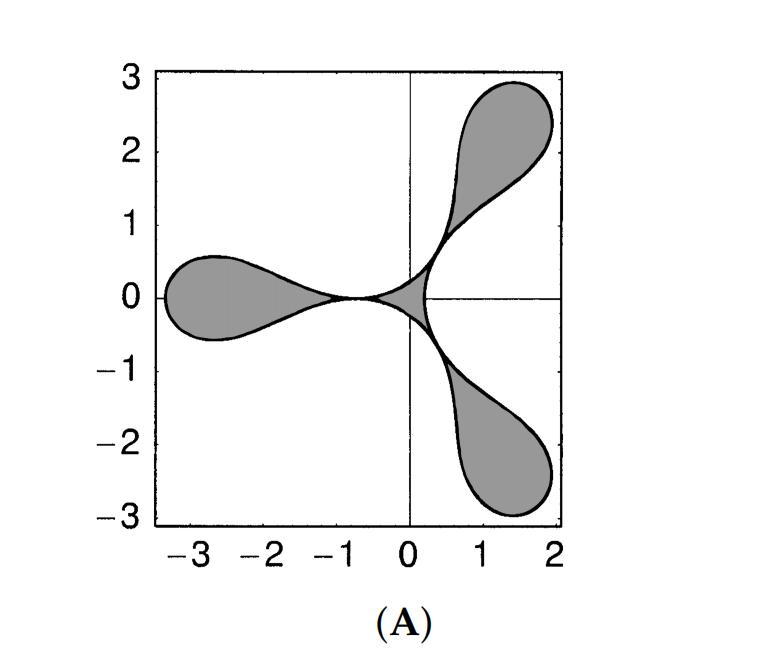
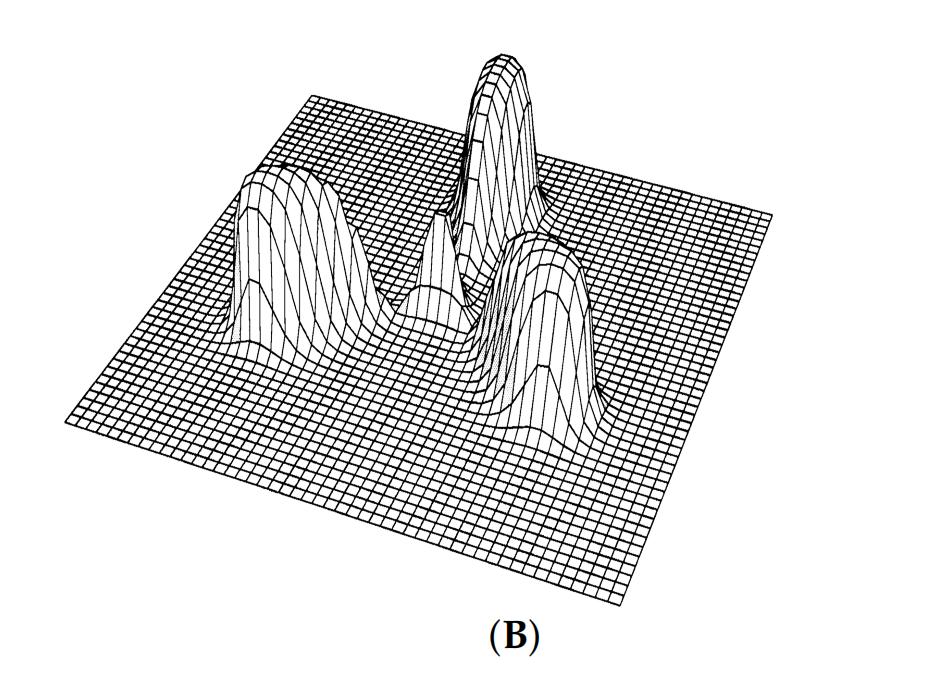
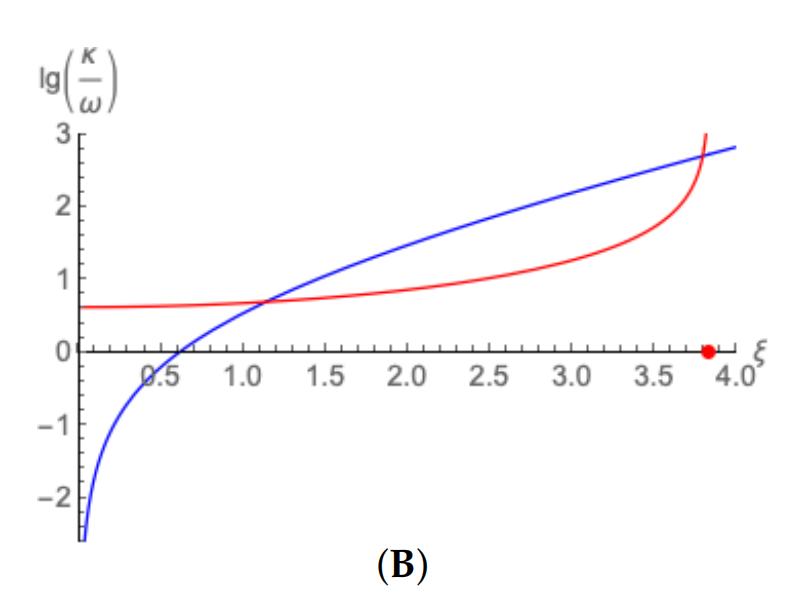
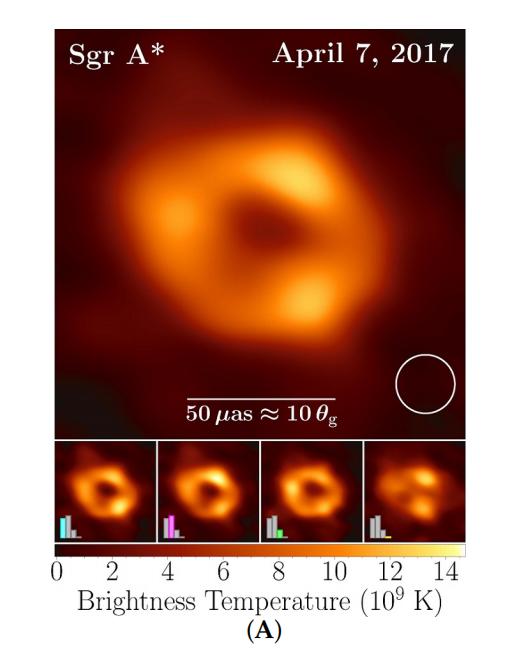
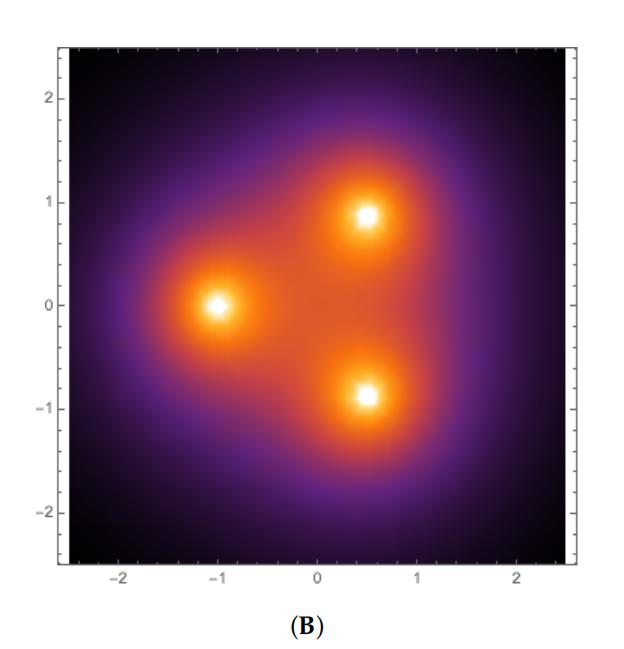
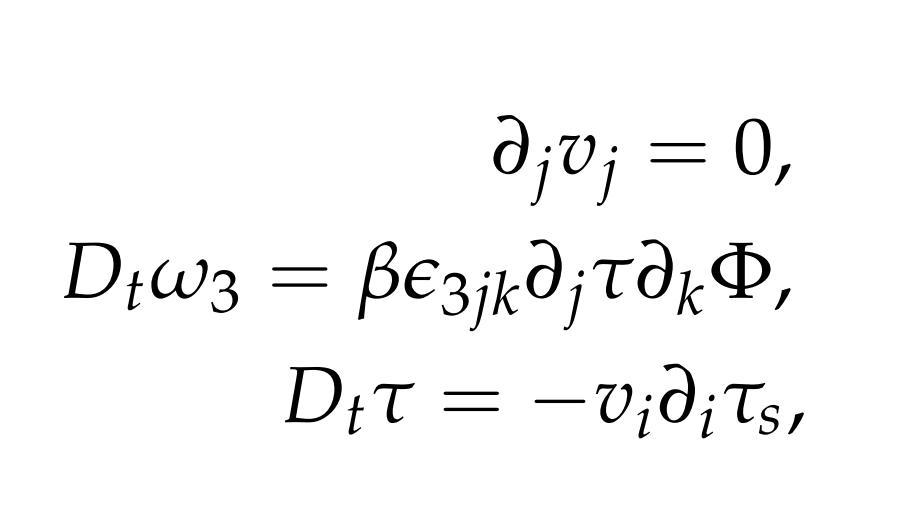r → ωr^2g/c的极限过渡，对黑洞Sgr A*吸积盘的2D准稳态演化     前言：由事件视界望远镜(EHT)合作拍摄的人马座A*的图像，揭示了其吸积盘内一个迷人的多点结构，这种结构，是先进的数据分析技术的结果，而不是简单的视觉观察。   通过检查和研究，科学家们已经能够辨别吸积盘内不同的点，虽然这种结构不是传统意义上的直接观察到的，但它是通过对世界各地各种望远镜收集的数据进行复杂分析而形成的，这个过程包括结合来自多个来源的数据，每个来源都提供了黑洞附近的独特视角。   在我们的研究中，我们将采用完全由黑洞的参数定义的时空度规，也就是它的质量和它的“自旋”，接下来，我们将做出一个至关重要的假设，与黑洞的“质量”相比，吸积盘的质量可以忽略不计，用m表示，这种近似适用于10^-5到10^-4乘以黑洞质量之间的值。   我们将假设吸积盘内的流体运动动力学不会受到辐射冷却的显著影响，这种简化允许我们关注系统的其他基本方面，可是，承认电子和离子之间通过库仑力的弱相互作用是很重要的，这种相互作用如此微弱，以至于可以认为电子和离子在很大程度上是相互去耦的。   因此，等离子体的电子和离子成分表现出不同的温度，电子比离子热，事实上，电子分量对吸积盘内物质的状态方程有最大的影响，电子和离子行为之间的这种区别是由于两种粒子之间显著的质量差异而产生的，轻得多的电子在等离子体中高度移动，导致等离子体整体上接近中性。   由于等离子体的高电导率，其自身的磁场可以被认为是“冻结”在等离子体中，这种现象对等离子体的行为有着重要的影响，因为它允许存在与周围物质密切相互作用的磁场，然而在黑洞物理学领域，描述这些天体附近的流体运动需要一个植根于相对论动力学原理的框架。   所以一开始，我们提出不带电黑洞Sgr A*周围的时空可以用克尔度规全面描述，这种度量作为爱因斯坦-希尔伯特方程的精确的、奇异的、稳定的、轴对称的解，该方程控制着真空中的引力“场”，这种度量标准的选择描述了黑洞对其周围环境的引力影响的复杂性。   为了导航这个时空景观，我们引入了Boyer-Lindquist四维坐标，记为q α = (t，r，θ，φ)，值得注意的是，虽然Boyer-Lindquist表示法是一种广泛使用的坐标系，但也可以使用时空位置的替代表示法。   在这些坐标的上下文中，表示为ds^2的区间的平方被表达为ds^2 = gαβ(r/rg，θ)dqαdqβ，其中α和β取值为0、1、2和3，这里，gαβ的分量只取决于无量纲组合rg/r和θ，在这种情况下，rg代表史瓦西半径，定义为2GM/c^2，g表示引力常数，m表示黑洞的“质量”，c表示光速。   特别重要的是度量张量中的非对角项g 03，这一项与黑洞本身的旋转速度有关，并与距离r成反比，对于一个一致的框架，我们采用带有公制签名diag的Minkowski张量，如包括Ref。   为了遵守运动物体的因果律，显然ds^2必须大于零(ds^2 > 0)，四个时空坐标q α = (t，r，θ，φ)共同指出了从远处有利位置观察到的世界事件的位置。   随着观察者从黑洞向外移动，过渡到极限r → rg和r → ωr^2g/c，空间坐标r、θ和φ的含义变得更加清晰，当ds^2接近它的极限形式c^2dt^2 dr^2 r^2(dθ^2+sin^2θdφ^2)时，从无穷远处看，这些参数可以解释为平坦时空中的标准球坐标。   然而，值得注意的是，参数r与黑洞中心的传统“距离”并不对应，在由方程ds^2 = gαβdqαdqβ描述的时空中，r = 0的中心点的概念在沿着任何物质对象的有效世界线的世界事件方面缺乏意义。   总结：本质上，上面概述的框架提供了一种使用相对论动力学原理和克尔度规描述黑洞附近流体运动的动力学和行为的严格方法，通过采用这种方法，我们可以更深入地了解黑洞引力对其周围环境的深远影响。   对于经历准2D流的理想流体薄层，另一种称为轮廓动力学方法(CDM)将连续的流体动力速度分布视为具有可移动边界(等高线)和内部恒定涡度的面片集合，这种近似法抓住了大规模流动的动力学和演化的一般趋势。   特别是当这种运动对速度场中的精细结构细节不太敏感时，描述二维流体中涡度-不连续性边界(轮廓)运动的轮廓动力学方程可以数值求解或解析求解，可是，Sgr A*吸积盘中热点的排列所示的热涡旋结构之间的相似性表明，所观察到的热点很有可能确实是大规模的准2D准稳态涡旋。   因此，理解这些现象的进一步进展取决于数值模拟的进展，背景温度、对比度、宏观结构尺寸、花瓣数、角速度、等离子体流梯度和特征存在时间等参数的可靠实验知识对于增强我们对这些有趣过程的理解至关重要。