数学的世界里充满了奇妙和出人意料的现象,而拓扑学便是其中之一。
作为一个在20世纪正式成形的数学分支,拓扑学主要研究那些可以自由变形的几何物体。尽管它的概念可以追溯至古希腊,拓扑学真正崛起并被广泛接受为纯数学的重要领域还是在最近一百年间。
它的理论本质使其在许多学科中得到了意外的应用,远超出数学的范畴。
我们可以将拓扑结构想象成一种能被拉伸、扭曲甚至揉皱的三维表面。
这些几何对象是拓扑学的核心元素。拓扑学家们发现,尽管对一个物体进行拉伸、弯曲等形变,很多几何特征仍然保持不变。
这种形变被称为“同胚变形”,意思是即便物体表面发生了形状变化,物体的“本质”依旧未变。

例如,将一个杯子变形为甜甜圈在拓扑学上是可能的,因为它们都有一个孔。想象一下,这就像在两者之间的无缝过渡,在拓扑学的定义下,它们是“同一类”物体。
不过,拓扑学对变形也有严格的限制。不能通过切割或将物体的部分重叠粘接来改变其形态。
这些限制使得不同类型的对象彼此保持区分,比如一个马克杯与一个甜甜圈有相同的“孔”特征,而与一个球形物体则不同,因为球体没有孔。这种基于孔数的分类被称为“物体的种类”。

在拓扑学中,以上的物体都属于“可定向曲面”,即它们拥有内外之分。球体有向内的表面和向外的表面,而马克杯和甜甜圈也能做类似的区分。但并非所有拓扑对象都具备这种特性。
你或许见过莫比乌斯环,它是拓扑学中一个经典的对象。只需将一张纸拧一下并将两端粘合,便能制作出一个莫比乌斯环。

莫比乌斯环
与可定向曲面不同,莫比乌斯环没有明确的内部或外部;在它上面绘制一条线,最后会发现这条线回到了起点,覆盖了整个表面,这在普通的球体上是不可能实现的。
电影《复仇者联盟:终局》中,托尼·斯塔克通过莫比乌斯环的结构探索了时间旅行模型。
在他开发的时间模型中,他对莫比乌斯环的运用触及了拓扑学的核心属性,但值得一提的是,莫比乌斯环因其不可定向性而无法被“翻转”,这也是拓扑学中的一个有趣点。

另一个不可定向曲面的例子是克莱因瓶。这种结构比莫比乌斯环更为复杂,且同样只有一个面。
克莱因瓶的表面没有边界,也没有内部或外部之分,它是拓扑学中一个引人入胜的研究对象。
正如数学家 Leo Moser 的打油诗描述的那样,“如果将两个莫比乌斯环边缘粘合,就会形成一个奇妙的克莱因瓶”。
拓扑学的理论在微生物学,特别是蛋白质折叠领域中展现了巨大价值。
蛋白质由成百上千的氨基酸组成,这些氨基酸通过相互作用形成特定的折叠结构,最终决定了蛋白质的功能。
生物学家利用拓扑学来理解蛋白质折叠的复杂过程:通过研究蛋白质在拓扑空间中的允许变化,他们可以预测其折叠方式。
拓扑学在蛋白质折叠中的应用虽然不能完全预测折叠方式,但却提供了蛋白质可能的相互作用方式清单,为生物学家在研究蛋白质结构上提供了重要的指导。
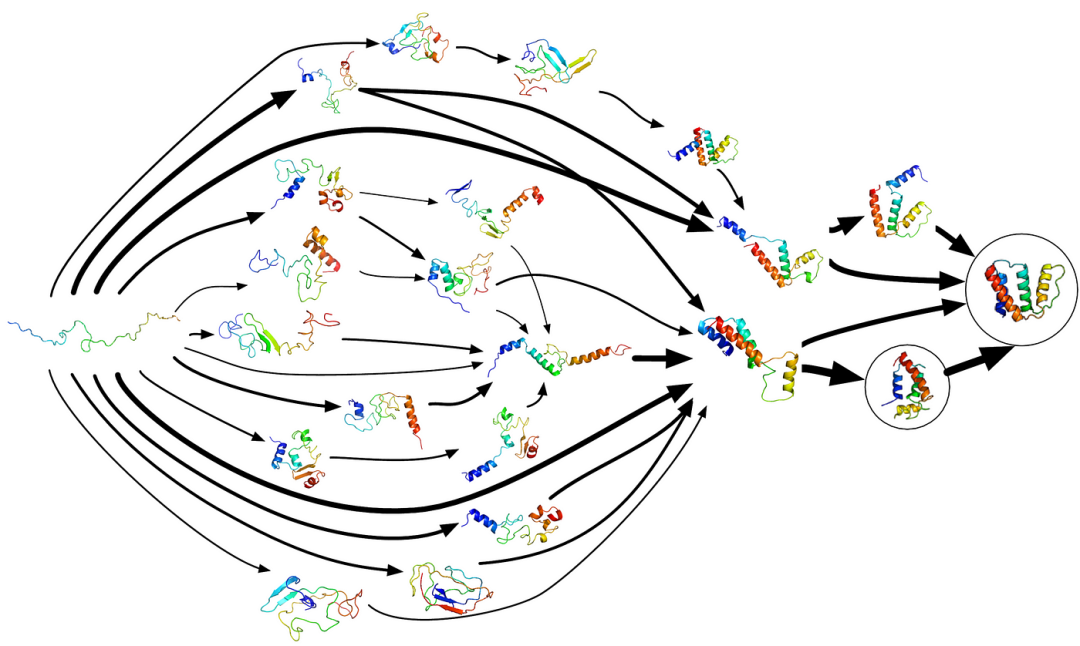
蛋白质折叠只是拓扑学在现实世界应用的冰山一角。计算机科学也常使用拓扑学对数据结构进行分类和排序。在物理学中,从凝聚态物理到宇宙学,都能看到拓扑学的影子。拓扑学的抽象理论为我们理解自然现象和解决复杂问题提供了全新的视角。
不得不说,拓扑学是数学中至关重要的分支,充满了奇妙的概念和出人意料的应用。