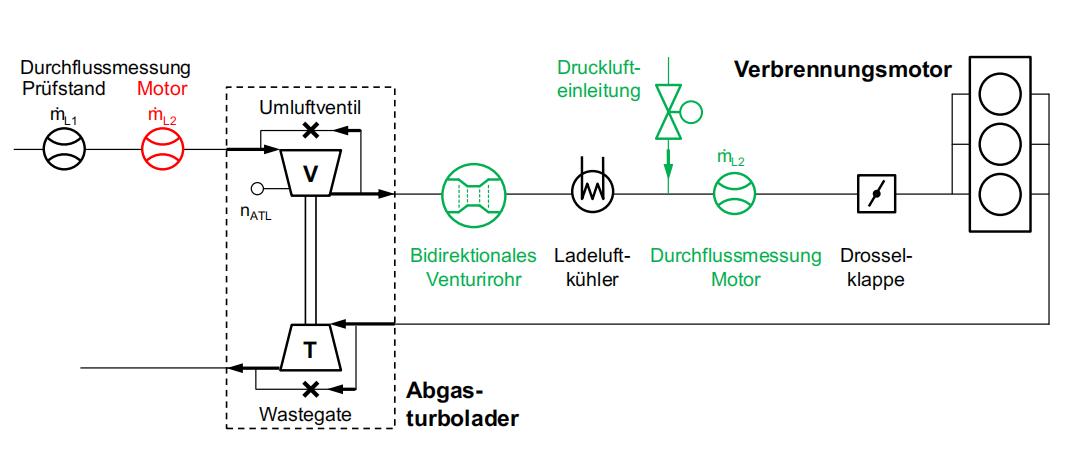
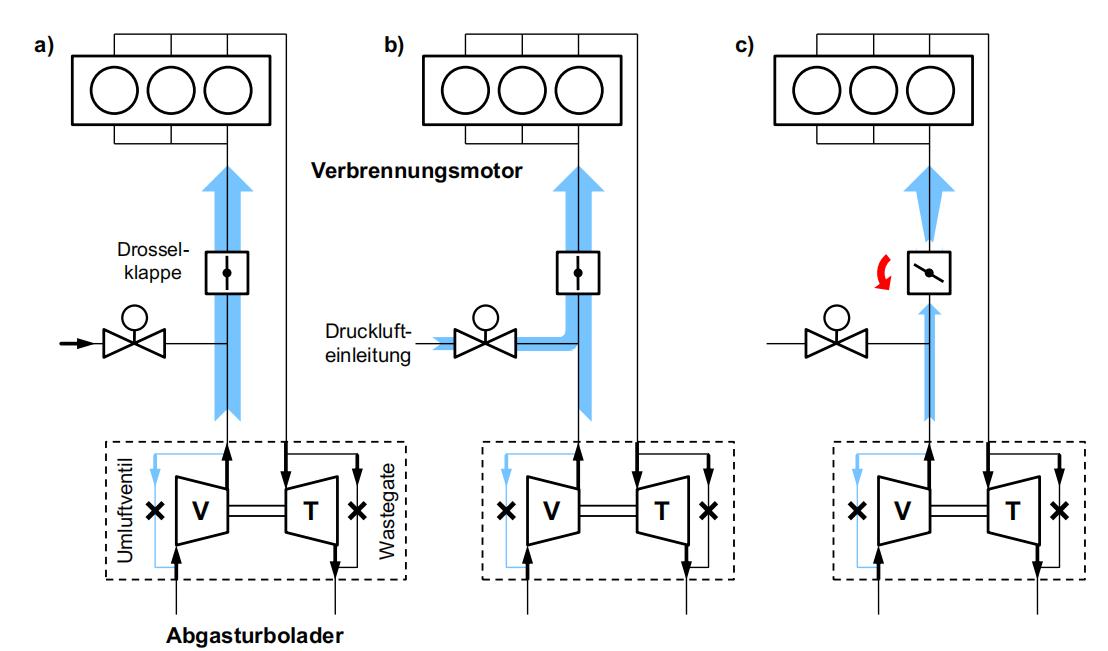
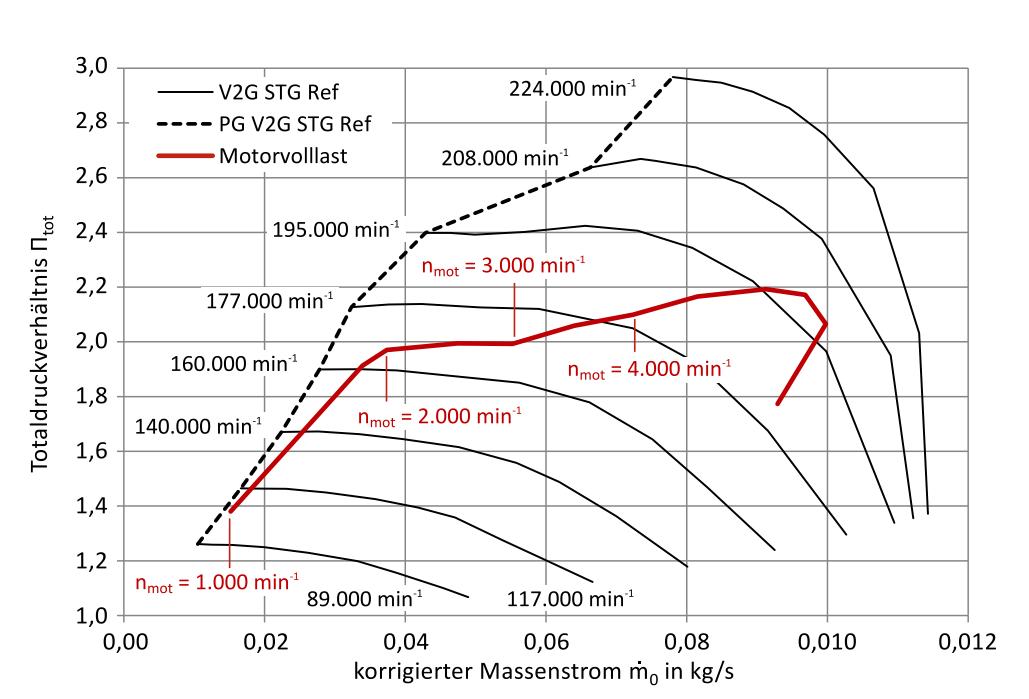
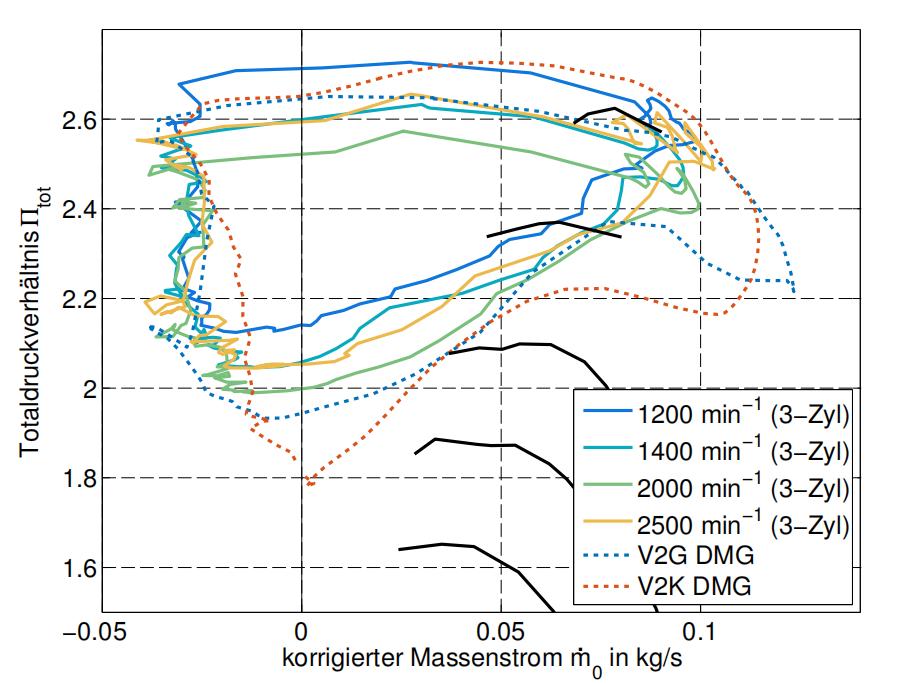
在高压缩机转速的泵限曲线PPC中，小型废气涡轮ETS如何才能发生耦合   前言：鉴于气候变化及其日益严重的影响，全球减少二氧化碳排放至关重要，降低排放水平的政治压力是通过具体的限值来施加的，在欧洲，新登记的乘用车的这些指标是由欧洲联盟的一项相应条例规定的，根据未来的发展调整这些指标通常伴随着更严格的目标。   因此，多年来，汽车业必须越来越多地专注于减少排放和燃料消耗，同时将废气涡轮增压器的两个动力装置--压缩机和涡轮--与内燃机相匹配。   然而，压缩机侧和涡轮侧不仅通过废气涡轮增压器轴直接耦合，而且通过燃气侧的内燃机间接耦合，因此不能相互独立地运行，同时，内燃机在其吞吐量方面具有不同的特性，所以在废气涡轮增压器上需要控制装置还是一个很困难的问题。   为了解决耦合问题，我们采用TRAUPEL的欧拉矩方程可以导出压实流体所需的关于压气机轮Yth∞4 压气机工作和不稳定性的具体理论工作。   在这种情况下，我们假设一方面没有流动损失（指数th），另一方面流动是叶片全等的（指数∞），这将与无限多的无限薄叶片有关，这个特定的理论叶轮功Yth∞是根据车轮的周向速度以及绝对速度cu1和cu2的周向分量计算出来的：Yth∞=u2·cu2−u1·cu1。   可是，如果假设理想的无旋流入流，使得圆周分量cu1=0成立，则方程简化为Yth∞=u2·cu2，具有图2.2中的几何关系，圆周分量cu2可以改写为子午线分量cm2和角度cu2=U2-Cm2 Tan·2的表达式，在方程中，对于特定的理论叶轮功Yth∞=u2，得到2−cm2 U2 Tan·2。   如果是在恒定的圆周速度u2和固定的结构尺寸·2的情况下，子午线分量cm2是压缩机流量的量度，对于选定的几何形状，它与输送的体积流量成正比：cm2‰V2，因此，Yth∞和V2之间存在线性关系，这描述了压缩机在恒定u2下的理论理想化特性。   不过，在实际条件下，假设的理想化必须被放弃，从而产生较低的比叶轮功Y，在恒定周向速度下，BOHL和ELMENDORF描述了以下损失分类及其计算方法。   由于流道的大部分区域存在非叶片全等流动，因此产生了低功率hmind，只有在压力侧叶片壁上，流动才精确地跟随叶片轮廓，损耗与Yth∞成正比，因此可以用@hmind=µmind·Yth∞估计。   摩擦损失随着渗透体积流量的增加而增加，在计算管道摩擦力的基础上，可以使用@hreib=µreib·C2 m2的方法。   冲击损失在设计点外记录，在设计点外，入射角与叶片角不匹配，随着与设计点的吞吐量差的增加，损失在两侧呈平方增加，在设计点cm2，a处使用车轮出口处的子午线分量进行估算，结果是：Hstop=µstop·（cm2−cm2，a）2，其中，间隙损失或泄漏导致特性曲线Y向较低体积流量的偏移，然而，具体的叶轮工作并没有减少。   在考虑损失的情况下，实际压缩机特性或因此，恒定圆周速度线或速度线是一条数学上下降到高吞吐量的曲线，但在低吞吐量下也可能具有正斜率，压力机特性的无量纲形式是压力系数ψ在流量系数φ上的应用，这两个指标都是通过与周向速度归一化来确定的。   但是在实际应用中，压缩机特性的另一种替代表示通常被使用，出于实用和说明性的原因，纵坐标总压力比·tot，使所提供的压力结构易于读取，总压比在测量和计算上也很容易确定。   在横坐标上，除了体积流量外，质量流量也可用于表示吞吐量，由于省略了圆周速度的归一化，经典的图表示包括几条恒定圆周速度或圆周速度的线，恒定的压缩机转速，以更高的转速可以实现更高的压力比。   为了表示速度n和流量量，这里是质量流量·m，与测量的环境条件无关，它们被归一化为参考值，这些计算出的吸力，“校正”值（索引0）使用参考值或参考温度Tbez和参考压力pbez，以及相应的环境参数Tumg和pumg，在试验台上使用Mach相似关系。   最终，在许多图谱中，等熵压缩机效率·is以等高线的形式输入到图的第三维中，最佳效率出现在设计点，该点通常位于图的中心，效率的其他等值线围绕该区域呈贝壳状运行，从相对的角度来看，每条速度线的最佳点位于其中间的可比位置。   总结：通过这次研究，我们的目的是更详细地研究小型排气涡轮增压器压缩机从稳定运行到不稳定运行的过渡，并根据参数表征不稳定运行。   对于主要的发动机控制，可以证明，在第一种情况下，压缩机工作点通过增加总压比接近泵限，在第二种情况下，这发生在总压比近似恒定和质量流量减小的情况下。   可是在发动机上无法分析高压缩机转速的泵限曲线PPC中，因为在发动机操作中，压缩机工作点远离该图区域，因此无法接近，不过，在未来，由于内燃机增压压力的总体趋势，这一操作范围的研究可能会变得更加重要。