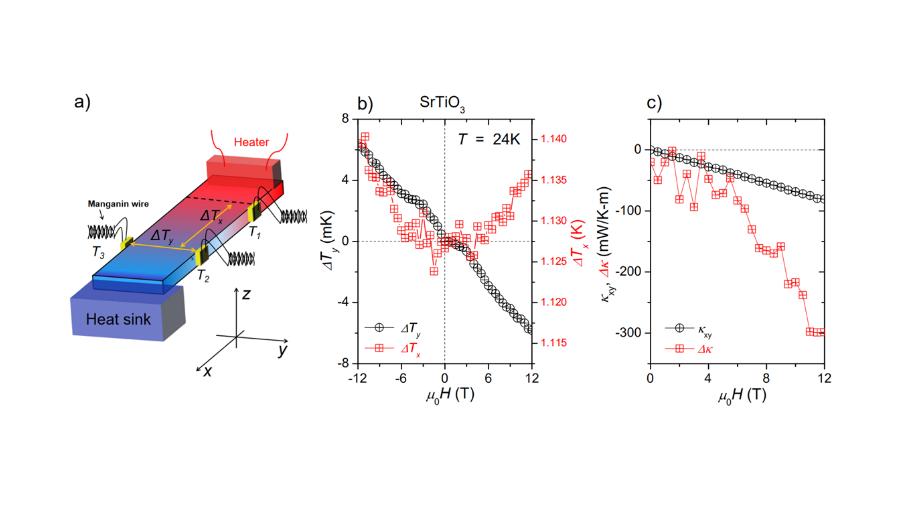
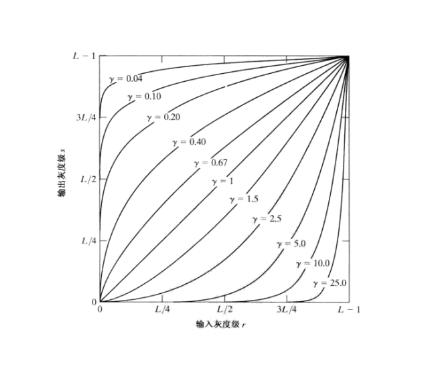
Tsallis玻色子气体在横向动量(pT)空间中的幂律压力该如何分布   前言：幂律分布经常应用于高能碰撞物理领域，特别是描述这些碰撞产生的粒子产额，而像π介子、k介子和质子这样的粒子，以及其他强子，在横向动量(pT)空间中呈现出明显的幂律分布，各种实验努力，包括STAR、PHENIX、ALICE和CMS，都利用幂律公式来描述这种分布。   对于该公式假设幂律横向动量分布的结构如下，\frac{d^2n}{dp_tdy} = p _ t \ frac { dn } { dy } \ frac {(n-1)(n-2)} { NC(NC+m0(n-2))} \ left(1+\ frac { mt-m0}{nc}\right)^{-n}。   在这个等式中，d^2N/dp_Tdyddy代表每单位横向动量和速度的粒子产额，p_TpT是粒子的横向动量，和dN/dydN/dy表示每单位快度的粒子产额。   参数nn, CC，以及m0m0在形成分配中起着至关重要的作用，指数nn影响分布的陡度，而CC和m0m0对整体曲率有贡献，该术语马太福音mT是粒子的横向质量。   幂律公式概括了高能碰撞事件中粒子产额、横向动量和快速性之间的复杂关系，它在不同实验中的应用强调了它在解开这些碰撞的潜在动力学和产生的粒子的特征方面的重要性，同时与克莱曼斯和Worku在2012年提出的横向动量分布的形式有一些对应，d 2N dpTdy = gV（2π）2 pTmT和_x0012_1 +（q−1）mT和−µT−qq−1。   这些等式引入了一系列参数，而参数在Tsallis统计力学框架内表征粒子分布时起着重要作用，比如说参数nn, CC, m0m0, VV(音量)，qq(Tsallis参数)，TT(Tsallis温度)，以及\muμ(化学势)是拟合参数，而gg代表退化，该术语mT = \sqrt{p_T^2 + m^2}mT=pT2+m2表示有质量的粒子的横向质量mm，以及yy代表快速。   这些分布与C. Tsallis在1988年提出的理论框架Tsallis统计力学有联系，这种统计方法已被证明在处理具有波动、长程相关性、小系统尺寸和分形结构的系统时是有效的，而等式d 2N dpTdy = gV（2π）2 pTmT和_x0012_1 +（q−1）mT和−µT−qq−1中呈现的分布充当Tsallis-2规定内的精确Tsallis类横向动量分布的零阶近似，这个特定的公式已经证明了它在大型强子对撞机(LHC)上描述现象的效用。   有趣的是，在研究中提出的q-对偶统计的概念中也可以出现相同的分布，它开创了Tsallis热力学探索的开创性，在类似Tsallis的经典和量子分布及其玻尔兹曼-吉布斯(BG)对应物之间进行了比较，当q参数接近1时，这些比较变得特别相关，导致Tsallis框架和更传统的Boltzmann-Gibbs统计之间的收敛。   幂律分布、Tsallis统计力学和传统统计方法之间的相互作用丰富了我们对高能碰撞中粒子分布的理解，它展示了Tsallis框架在处理各种物理场景方面的多功能性，以及它在适当条件下弥合经典和量子统计力学之间差距的能力。   本次研究概述了与Tsallis热力学相关的研究及其在推进以波动和长程关联为特征的系统相关研究中的潜在意义，特别是在夸克-胶子等离子体和其他类似系统的背景下，该论述还深入研究了这些现有发现延伸到量子领域的全面描述。   其中，研究采用的方法包括利用幂律函数的轮廓积分表示，并遵循方程中的方法，通过将量子分布表示为经典麦克斯韦-玻尔兹曼(MB)分布的无穷和，照亮了通往量子域的路径，在Tsallis统计的指导下，对玻色子气体压力的分析测定进行了细致的阐述，而压力的最终表达式采用求和的形式，由经典分布的合并而产生。   但是可以观察到，在研究中探索的例子只需要有限数量的项就可以精确收敛，在保持参数不变的情况下，所需的项数随着质量的增加而减少qq和TT不变，被称为梅林-巴恩斯表示法的积分表示法在论述中占有重要地位，其根源在于量子场论循环计算，这个例子强调了不同研究领域之间的技术交叉，说明了一个领域中建立的方法如何有助于另一个领域的进步。   结论：虽然讨论主要集中在玻色子的情况下，但值得注意的是，将分析扩展到费米子的情况是直截了当的，关键的区别在于求和，其中每一项都包含一个因子(-1)^{s+1}(−1)s+1。   因此，在我们的研究中，最终结果主要集中在类Tsallis玻色子气体的压力上，或许这样一个系统的其他热力学性质可以通过适当地微分压力函数来推导，但这种全面的探索不仅阐明了Tsallis统计和量子力学之间错综复杂的相互作用，而且为进一步研究显示长程相关性和波动的不同系统的热力学奠定了基础。