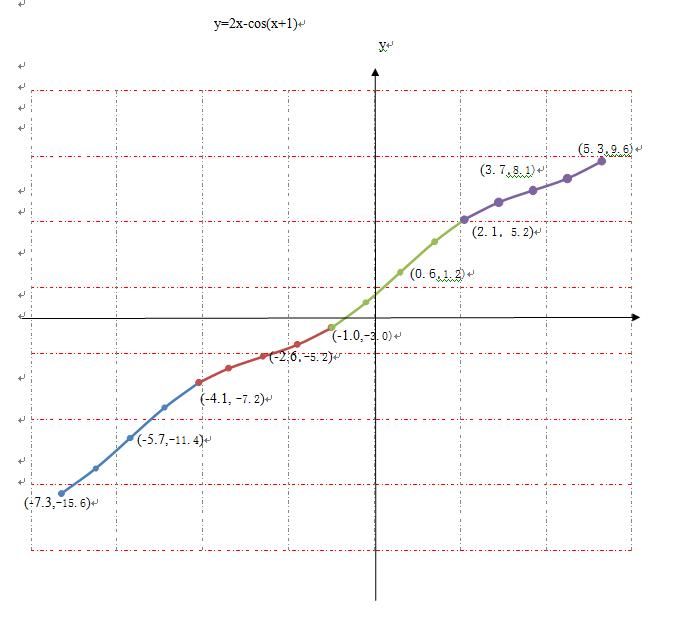
本文介绍三角函数y=2x-cos(x+1)的定义域、单调性、凸凹性等函数性质，并通过导数知识求解函数的凸凹区间，简要画出函数在[-(2π+1),(2π-1)]区间上的图像示意图。

根据函数的特征，函数是一次函数y1=2x和余弦函数y2=cos(x+1)的和函数，且二者的定义域为全体实数，所以其和函数的定义域也为全体实数，即为(-∞，+∞)。

本题用导数知识来判断函数的单调性并求解函数的单调区间。

因为y=2x-cos(x+1),两边同时求导有：

所以dy/dx=2+sin(x+1),

因为|sin(x+1)|≤1，则dy/dx≥2-1=1>0.

则函数y为增函数。

本题用导数知识来判断函数的凸凹性并求解函数的凸凹区间。

因为dy/dx=2+sin(x+1)，再次对x求导有：

所以d^2y/dx^2=cos(x+1)，

令d^2y/dx^2=0，则cos(x+1)=0，即：

x+1=kπ+π/2，k∈Z.

结合本题限制区间[-(2π+1),(2π-1)]，

即x+1∈[-2π，2π],所以此时有k=-2，-1，0，1，

分别对应1x+1=-3π/2，-π/2，π/2，3π/2，

进一步求出x对应为：-(3π+2)/2，-(π+2)/2，(π-2)/2，(3π-2)/2；

所以函数的凸凹区间为：

(1)当x在[-(3π+2)/2,-(π+2)/2]∪[(π-2)/2，(3π-2)/2]时，d^2y/dx^2<0,此时函数y为凸函数;

(2)当x在[-(2π+1), -(3π+2)/2]∪[-(π+2)/2，(π-2)/2]∪[(3π-2)/2, (2π-1)]时，d^2y/dx^2>0,此时函数y为凹函数。

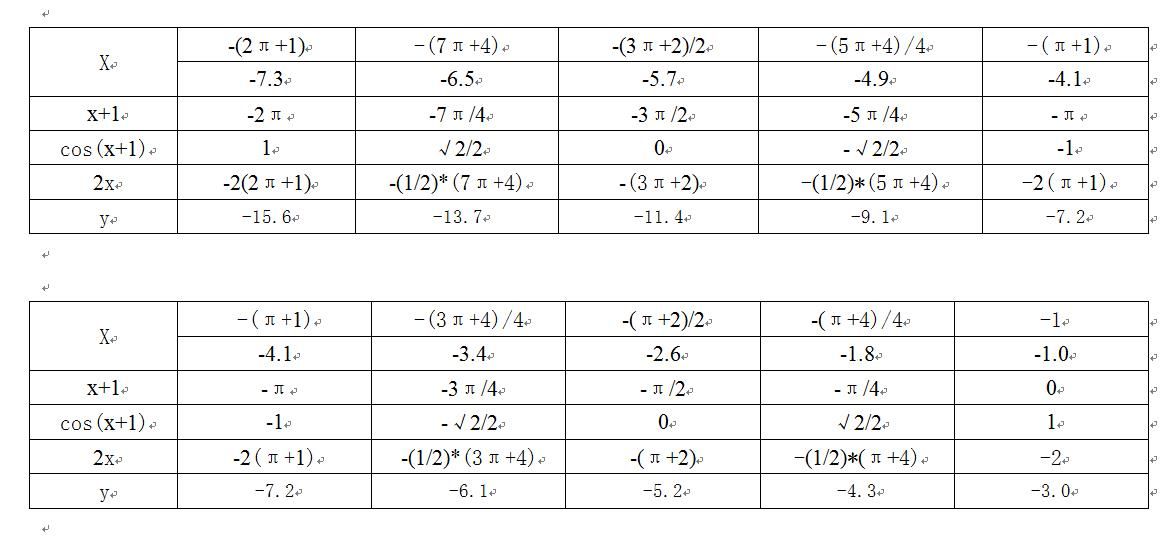
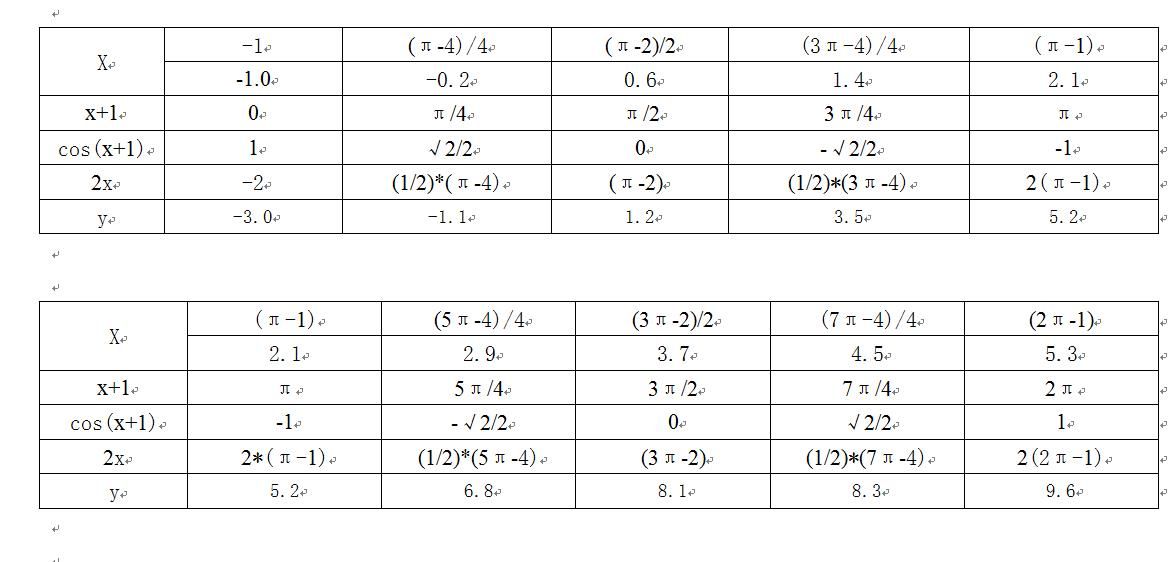
※.函数的部分点图