光年，是个距离的量度，并非时间的尺度。它指的是光线一年所穿越的距离，大约为9.46万亿公里。对地球居民而言，光年之遥，几乎遥不可及。

宇宙之浩渺，用公里来度量显得过于微小，因此我们采用了光年这个更大的尺度。然而，即便是光年，置于宇宙的巨大尺度中，也是显得如此渺小。

光年的定义似乎不难理解，但为了严谨，我们需要深入探讨。你可能会质疑，一光年的定义是光线行走一年的距离，难道这距离真的需要光线走一年吗？这个问题听上去有点复杂，像是在辩论，但它并不是。光年确实是光线一年所经过的路程，这一点无误，但光线走完一光年的距离，并不需要整整一年。

如何理解呢？我们需要明确：光线行走一年所经过的距离叫做光年，这里“一年”是相对于我们人类的时间，而非光线自己的一年！理解这一点很关键。

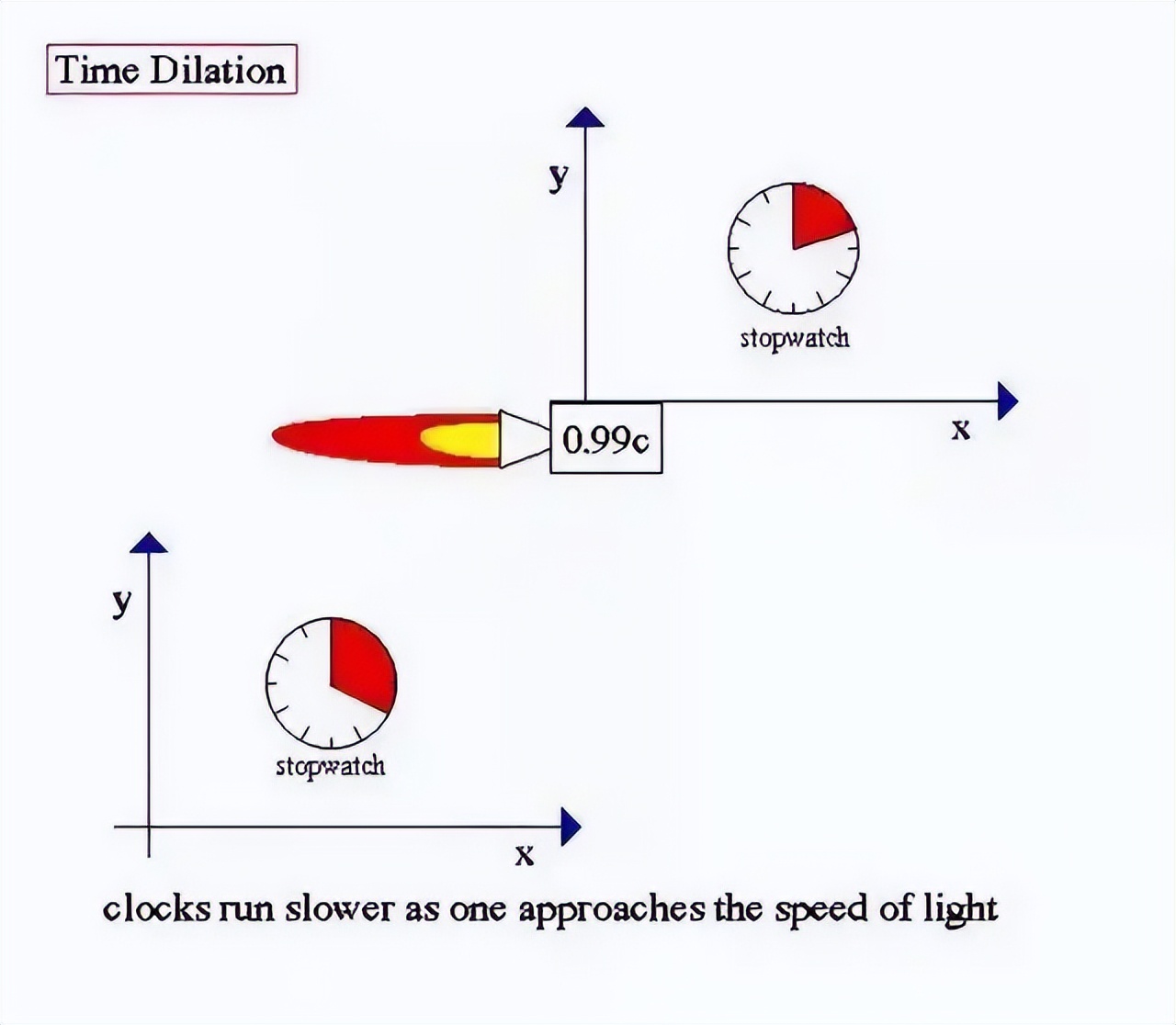
根据爱因斯坦的狭义相对论，一个物体的速度越接近光速，其时间流逝的速度就会越慢，这就是所谓的“时间膨胀效应”。具有静质量的物体永远无法达到光速，只能是无限接近。一旦物体速度等同于光速，那么它已经变成了光子，不再是原本的物体。

为何有静质量的物体不能达到光速呢？狭义相对论的质速公式可以给出答案：

公式中的m是物体的质量，m0是其静质量，V是物体的运动速度，c代表光速。从公式可以看出，当V无限接近光速，物体的质量会趋近于无穷大，这意味着需要无限多的能量来驱动物体保持这个速度，这显然是不可能的，尤其对于有限的宇宙而言更是如此。

光速不变原理是狭义相对论的两大基本假设之一，它意味着光速在任何参照系中都是常数。通常我们讲速度时必须设定一个参照系，否则速度无从谈起。然而，光速是个例外，它不需要参照系（或在任何参照系中都是光速），这使光速成为时空的基本属性，严格来讲，光速并不是指光的移动速度，而是由麦克斯韦方程组推导出的一个常数，与真空的磁导率和介电常数有关。

关于这一点，我们稍后再谈。

理解了光速的这一特性，我们就能明白，对于光线本身而言，没有时间的概念。换句话说，无论光线穿越的距离有多远，对于光线来说，都是瞬间即达，即便是穿越整个可观测宇宙，也只需一瞬间。

然而，在人类的视角中，情况并非如此。光线走完一光年的距离，的确需要一年的时间。这是由于不同参照系的选择导致的不同认知。

理解这一点可能有点困难，那我们就用亚光速旅行来举例说明。

如果你乘坐一艘亚光速的飞船离开地球，你在飞船上度过的一年与地球上的我度过的一年是不同的。各自经历的时间（本证时间）是相同的，这意味着你体验到的一年与我体验到的一年在长度上是一致的。这并不矛盾，而是参照系的不同选择所带来的结果，体现出时间的相对性和同时的相对性。

换句话说，对于两个不同的参照系，对同一事件的时间观察结果是不同的。

例如，比邻星距离地球约4.3光年。如果你乘坐亚光速飞船飞向比邻星，地球上的我看来，你需要大约4.3年的时间才能到达。但对于飞船上的你来说，所需的时间远少于4.3光年。

在亚光速旅行中，时空的变化非常显著，尺缩效应也变得非常明显。地球与比邻星之间的距离不再是4.3光年那么远，实际上会比这个距离更短，具体缩短的程度取决于你与光速的接近程度。理论上，比邻星甚至可能就在你眼前，你可以瞬间到达，前提是你必须非常接近光速。

当然，也可以理解为速度越快，所花费的时间就越短，因为时间膨胀效应和尺缩效应是相辅相成的，时间和空间本就是不可分割的整体。

这其中涉及到一个类似“双生子佯谬”的问题。

从地球上的我的视角来看，你飞往比邻星需要4.3年。而你却觉得自己远不到4.3光年就能到达，我会看到你的时钟变慢了，你的所有动作都放慢了，就像电影中的慢动作一样。

由于速度具有相对性，你看我的效果也一样，你会看到我的时钟同样变慢了，我的一切动作也都慢了下来。

那么，到底谁的时间变慢了？看起来似乎存在矛盾。

实际上，并不矛盾。因为我们处于两个不同的参照系中，你和我观察到的结果仅代表各自的参照系，无论如何，都不会发生矛盾，我们的观察结果都是正确的。

那么，为何亚光速飞行的你会显得更年轻呢？

“年轻”这个概念也是相对的。也就是说，你和我必须重新回到同一个参照系，才有资格比较谁更年轻。如果我们一直处于不同的参照系（永远不返回地球），那么讨论“谁更年轻”就没有意义。因此，你必须返回地球，然后才能比较谁更年轻。

如果你打算返回地球，势必会经历减速和加速的过程，这个过程实际上改变了你的时间，让你的时间变慢了。而我，地球上的我，并未经历减速或加速。

有一个公式可以用来计算你的时间相对于我的时间到底慢了多少，这个公式如下：

最后强调，在任何参照系中，个体感受到的时间（本证时间）都是相同的，没有任何区别。