文/福星徕
编辑/福星徕
前言
控制粘弹性流体流动是当前流体力学领域的一个重要方向,仿射和非仿射粘弹性流体作为一类特殊的粘性流体,在液体和固体行为之间存在着复杂的相互作用。
通过对流体流动的控制,可以实现对粘弹性流体在科学方面的应用,如降低能源消耗、改善制造过程、增强材料性能等。为了理解和预测粘弹性流体流动的行为,并设计有效的流动控制策略,建立控制方程组和分析其无量纲形式是必要的。

将方程组进行无量纲化处理可以简化方程的形式,改变方程的形式使其更适合数值求解和分析。将引入适当的无量纲变量,并通过选择合适的参考长度、时间和速度等无量纲参数,将控制方程组转化为无量纲形式。
通过对仿射和非仿射粘弹性流体流动的控制方程组和无量纲形式的分析和求解,可以深入了解粘弹性流体的行为,为流体流动的控制提供依据,这对于优化流体力学系统以及开发新的流体控制技术有非凡的意义。
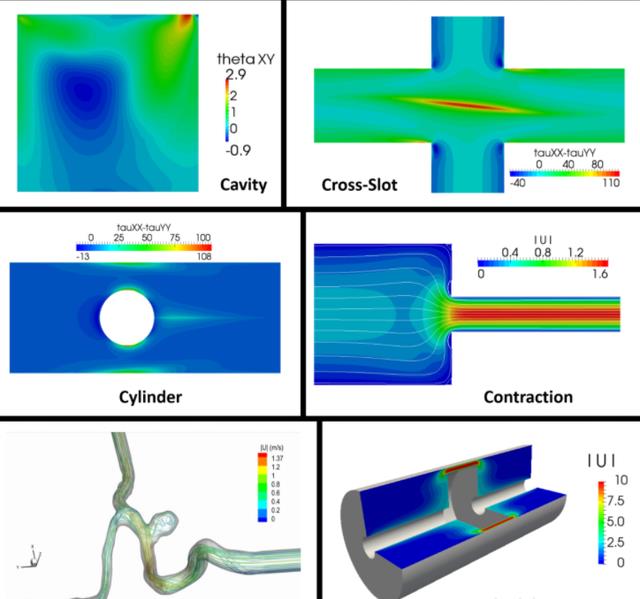
在质量守恒和动量守恒方程中,添加一个线性的本构方程,例如Oldroyd-B模型,或非线性的本构方程,如Giesekus模型或PTT模型,会大大复杂化粘弹性流体流动问题的数学分析,从而使数值模拟变得困难。
这类问题的偏微分方程系统的非线性性质,使得完整的数学理论关于解的存在性和唯一性得以建立变得困难。然而,了解控制粘弹性流体流动的方程系统的数学结构和数学特性对于开发适当的数值解法以及确定良好定义的数学问题所需的初始条件和边界条件非常重要。
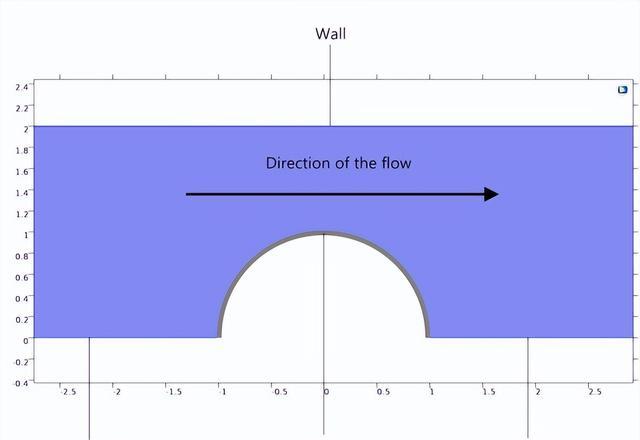
为了构建一个稳健的数值算法,用于求解依赖时间且不可压缩的粘弹性流体流动的方程系统,需要了解这种方程系统的数学结构并确定其所属的方程类型。方程类型的概念通过观察方程对小扰动波的响应,提供了关于方程系统性质的指示。
如果受控波只是在计算域中以有限速度传播,那么偏微分方程被称为双曲型。如果波被方程系统阻尼,那么方程类型被称为抛物型。如果波的传播速度是无限的(非实数),方程类型为椭圆型。
因此总结对方程类型的分析,基于Fourier方法,一般的Oldroyd类粘弹性模型证明了由动量方程和本构方程构成的一维齐次方程组的双曲性,并给出了这类方程组的双曲性条件,以此给出了组成控制方程组的各部分的初始条件和适当的边界条件。
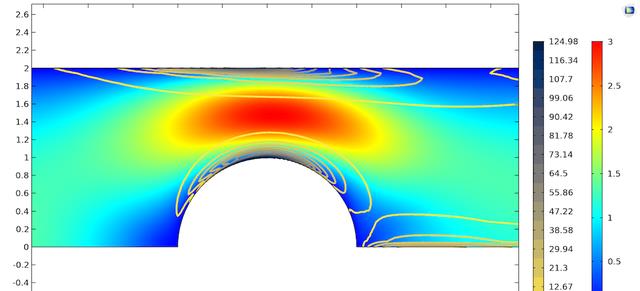
数学模型
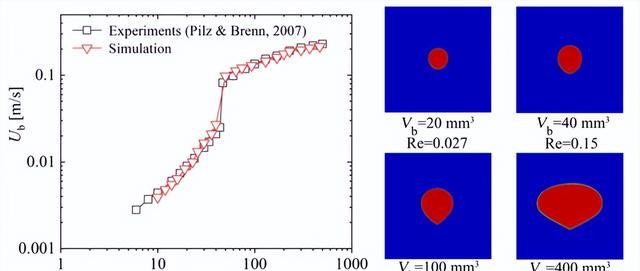
考虑粘弹性聚合物流体在边缘范围内的不可压缩,时间相关和各向异性流动。这种流动由包含超应力张量的质量,能量和动量守恒方程描述:

在上述方程中,u=(u1, u2, u3)是速度向量,p表示总应力张量的等向部分,T是额外应力张量,T是温度,ρ是体积质量,k是热导率,Cp是比热容。
在工作中,额外应力张量T被表示为溶剂的牛顿贡献2ηsD和聚合物贡献τ的和:

其中D是应变速率张量,ηs是溶剂的粘度。额外应力张量τ与应变速率张量之间的关系由一个本构方程给出:
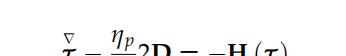
其中符号 () 表示上述所写的上导数。
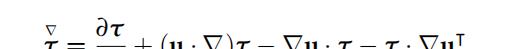
其中ηp表示零剪切速率下的聚合物粘度,λ是流体的弛豫时间,项H用于将多个流变模型进行组合,即UCM,Oldroyd-B,Giesekus,SPTT,Johnson-Segalman和PTT。张量函数H写成,张量函数H可以表示为:

除PTT和Johnson-Segalman模型外,所有其他模型,即Oldroyd-B,Giesekus和SPTT的滑移参数为零。注意,Gordon Schowalter的目标导数被简化为上对流导数。
另外,能量方程右侧的最后一项代表能量耗散,即:

它具有溶剂的牛顿原点和外应力张量的聚合原点。
控制方程的无量纲化
为了引入控制方程的无因次版本,考虑长度特征尺度L、速度尺度U和温度差ΔT = T0 - T1。在管道内流动的情况下,根据温度边界条件,该问题将在之后进行讨论。其中T0是参考温度(通道入口处的温度),T1是壁面温度:

为了简化方程的写法,在后面的部分中省略无因次变量上的横线。质量守恒方程(2.1a)、动量守恒方程(2.1b)和能量方程(2.1c)的无因次形式如下所示:
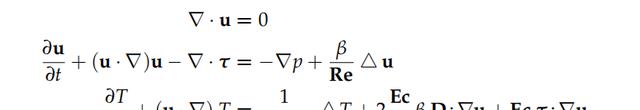
本构方程以无量纲形式表示:


对于简单流动,弹性力的主要作用是法向应力差N1 = τ11 - τ22,而聚合物粘性力与聚合物剪切应力τ12有关:

Oldroyd-B、Giesekus和PTT等类型的流变模型预测,第一正应力差N1与N1~ληp˙γ^2成正比,剪切应力τ12与τ12~ηp˙γ成正比。
在这种情况下,魏森伯格数可以被解释为与牛顿流体行为相比的粘弹性行为的度量。它由松弛时间λ,用于描述流体非线性响应的时间,乘以平均剪切速率的倒数(代表流动的特征时间的倒数)˙γ = U / L得到。魏森伯格数化简为:

高稀释度的聚合物溶液具有非常短的松弛时间,因此魏森伯格数接近于零。相反,高交联聚合物和浓缩聚合物溶液具有较长的松弛时间,通常具有较大的魏森伯格数。
方程组分类
对描述二维粘弹性流动问题的Oldroyd-B类本构方程进行基于方程类型的系统方程分类,这适用于稳态和非稳态问题,并强调了识别规定方程类型的重要性。数学分析系统方程的主要步骤是根据方程类型进行分类,以及对系统方程的Hadamard意义下的演化性质进行求解。
从数值角度来看,分类能够提供重要的信息,不仅对于开发、构建和应用适合系统方程性质的数值离散化方法至关重要,还能确定边界条件和所需的初始条件,以获取一个良定义的问题。

对于独立于时间t的问题,如Stokes流动、热传导、粘性流体的层流流动、弹性问题等,已知它们构成椭圆型方程系统。例如,在稳态下的标量φ扩散问题中,D?φ+f=0,其中D是扩散系数,f是源项,这是一个椭圆型问题,需要在域的所有边界上给出边界条件。
与独立于时间的问题相反,非稳态问题引起的方程系统要么是抛物型的,要么是双曲型的。实际上,耗散性问题通常由抛物型方程系统导致,并在稳态下变为椭圆型。在这种情况下,方程系统的解在时间上传播,在空间中扩散,例如非稳态扩散方程?φ/?t = D?φ + f。

另一方面,纯对流方程?φ/?t = a?φ/?x,其中a是对流速度,以及波动方程,都是双曲型的。双曲型方程系统的特点是沿着一些实特征速度,特征变量会随时间演化。解决这种类型的方程系统需要为进入域中的特征量规定初始条件和边界条件。
由于纯对流方程没有任何耗散机制,所以初始解中或边缘上的所有不连续性都将沿着特征保持不变。在这个意义上,椭圆问题可以看作是波传播速度无限的双曲问题,椭圆变量在域内的演化与其在边的值直接相关。

由于纯对流方程缺乏耗散机制,解的初始不连续性或边界不连续性将沿着特征线被保持。从这个意义上讲,可以将椭圆型问题视为具有无限传播速度的双曲型问题,而椭圆型问题中变量在域内的演化直接与其在边界处的值相关联。
Navier-Stokes方程描述了牛顿流体的等温、不可压缩流动,其类型主要是:在稳态下是双重椭圆型的,在时间相关的非稳态下是基本上是椭圆-抛物型的。
Navier-Stokes方程的抛物部分源于随时间演化的牛顿分子扩散,而椭圆部分则源于不可压缩性约束,该约束在任意时刻都满足?·u = 0,这意味着?(?·u)/?t=0。动量方程可以重新表述为以下形式:

从这个角度来看,压力p出现在动量方程中是为了满足不可压缩条件。换句话说,对方程进行散度运算得到了泊松方程,用于描述压力,即:
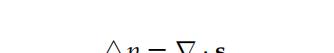
该方程显示了Navier-Stokes方程具有椭圆性质,此外,对于不可压缩且非等温的牛顿流体流动,添加能量方程不会改变所统治方程组的类型。事实上,能量方程是一个对流扩散方程。
然而,在稳态下,它基本上是椭圆型的,在非稳态下是抛物型的,整个统治方程系统仍然是椭圆-抛物型的。

在涉及非压缩和非等温的粘弹性聚合物流体流动中,系统除了能量方程外,还包括一条本构方程,该方程是准线性(UCM和Oldroyd-B模型)或非线性(Giesekus和PTT模型)差分方程。
本构方程是双曲型的,因为它不包括耗散项。同时,该方程组既不严格是双曲型,也不严格是椭圆型。

控制方程组的方程类型
有两种主要方法,可用于将控制粘弹性流体的不可压缩且等温流动的偏微分方程系统按方程类型进行分类。
第一种方法是间断导数方法,其中确定方程系统类型的评估基于特征曲面的确定。第二种方法是将方程系统重新写成傅里叶变换空间,并使用低振幅波的稳定性分析来评估方程系统的类型。
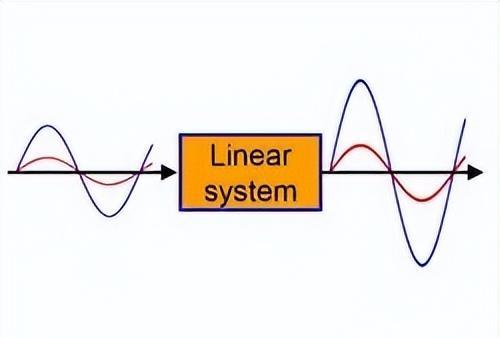
该方法既用于分析控制粘弹性流体流动问题的系统的演化特性,也用于分析方程系统的类型。系统方程的类型是由全局微分算子的主要符号部分确定的:该符号可以被解释为系统对特定解的响应。事实上,所施加的解,会以平面波的形式给出。
使用第二种方法(傅里叶变换)进行了分析,以确定UCM模型的方程系统类型。需要注意的是,UCM和Johnson-Segalman等本构模型不包括溶剂粘度,因此速度场没有出现二阶导数。
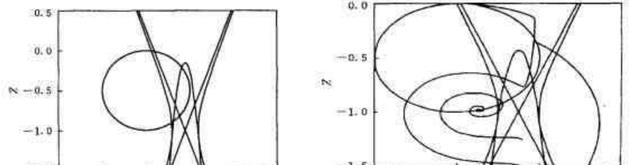
当在动量方程中出现二阶导数时,可以将这种方法扩展到其他模型,例如Oldroyd-B和PTT。对此进行了二维稳定性分析,涵盖了方程系统的所有变量,即w=[p, u1, u2, τ11,τ12,τ22]。
为了更好地说明该方法,选择2D SPTT模型作为示例,并将其设置为以下形式:
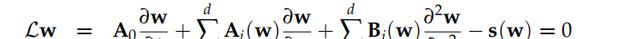
在二维的情况下,对于差分算子L(x, t, ?/?xi, ?2/?x2i)中的矩阵Ai、Bi和s,具体如下:

在这些矩阵中,系数Ai、Bi和s依赖于空间变量x、时间变量t,以及一阶导数 (?/?xi) 和二阶导数 (?2/?x2i)。其中的s1、s2等项代表由SPTT模型的参数e控制的特定弛豫和非线性项。
在小幅振幅傅里叶波动稳定性分析中,对于所统治的方程系统,假设的解以传播方向κ为平面波的形式给出:
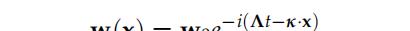
在傅里叶变换空间中,根据稳定性分析,假设解的分解形式为平面波,其中Λ代表频率(或特征值),κ = κ1e1 + κ2e2表示波矢向量(或傅里叶变量),而e1和e2是沿空间方向的单位向量。
这种将解表示为平面波(2.16式)的线性组合,使得能够重新写出作用于变量向量的线性微分算子在傅里叶变换空间中的形式:对于一阶导数,有?/?x1 = iκ1和?/?x2 = iκ2;对于二阶导数,有?2/?x21 = -κ21和?2/?x22 = -κ22。因此,将方程转化为:

如果符号的行列式为零,那么方程在所有波矢κ的方向上会存在一个非平凡解w:

详细计算得出以下多项式:


其中,实根确定了所统治方程系统的特征。该多项式的主要部分对应于关于κ的最高次数:
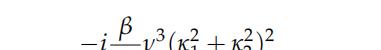
而构成主要部分的因素为以下几种:
椭圆部分对应于应力无压缩约束所产生的拉普拉斯算子的符号,即梯度压力的散度算子应用后的结果。这个椭圆部分不依赖于时间。然而值得注意的是,当允许稍微可压缩的流动时,这个部分可以完全变成双曲型。

抛物线部分与Navier-Stokes方程的主要符号部分相同,与非定常流动状态下的溶剂粘度相关的拉普拉斯算子的符号相对应。当稳态建立时,它变成椭圆型。
需要注意的是,承担着连接动量方程和本构方程的作用的因子与剪切弹性波的传播有关。在UCM流体的框架下,这个因子被Joseph等人与涡度方程的符号相关联,事实上,在时域上,它是双曲型的。

在稳态条件下,这个因子导致了在UCM流体的Stokes流动中涡度方程的“类型转变”机制。此外,通过方程发现,与SPTT模型、UCM模型和Oldroyd-B模型(e = 0)的相关项s不对系统方程的主要部分做出贡献。
对于Giesekus流体来说,由于在本构方程中非线性模型项的贡献并不相同,导致得到的特征方程表达式比方程更加复杂。
然而,控制Giesekus流体的系统方程的主要符号部分与控制SPTT流体的方程类似。对于PTT和JS模型来说,包含一阶导数的滑移项ξ(Dτ+τD)参与到双曲线部分中,并影响系统方程的实际特征。由于计算复杂性,非线性项和滑移项将在准线性齐次系统中被排除,并作为源项进行处理。
总结起来,描述时间依赖且不可压缩的粘弹性聚合物流体流动的方程系统由质量守恒方程、动量守恒方程以及与诸如Oldroyd-B模型、SPTT模型、JS模型、Giesekus模型或者PTT模型等流变学模型相关的方程组成,具有混合类型的特点:椭圆/抛物线/双曲线。

其中,椭圆部分与不可压缩性约束和速压耦合有关。抛物线部分与溶剂的分子扩散相关。双曲线部分是由方程的构成引入的速度-应力耦合,其特点是存在一定数量的实际特征速度,沿着流线传递相应的特征变量,并可呈现为弹性剪切波的传播形式。
对于对流-扩散能量方程(抛物线类型)、动量分子扩散(抛物线类型)以及速度-压力耦合(椭圆类型)的处理已被广泛使用的经典方法(如有限差分法或有限体积法)处理,并且通常不会带来困难。数值分析粘弹性流体流动的困难主要在于处理双曲线部分。

因此,了解与特征速度相关的特征变量的数量和表达式对于选择适当的数值离散化方法以及规定边界条件中的特征变量至关重要。
如已知,对于抛物线/椭圆型问题而言适用的数值方法在应用于双曲型问题时会导致灾难性的数值振荡。因此,有必要清楚地确定双曲型部分及其双曲性域,以应用适当的数值处理方法。
为了分离双曲型部分并确定特征变量,提出对方程系统进行傅里叶分析的方法,从中排除抛物线/椭圆部分、弛豫项和非线性项。
结论
通过推导控制方程组和将其转化为无量纲形式,揭示了粘弹性流体流动的基本特性以及控制方程组的形式。发现控制方程组的方程类型对于粘弹性流体流动的理解和控制具有重要的作用。
根据流体的黏性和弹性特性,确定了适用于仿射和非仿射粘弹性流体的不同方程模型。这些方程模型包括黏性流体的Navier-Stokes方程和弹性流体的Maxwell方程、Oldroyd-B方程等。

同时,还对控制方程组进行了无量纲化处理。通过选择适当的参考参数,将控制方程组转化为无量纲形式,从而简化了方程的形式,方便了数值求解和理论分析,这样的转化可以更深入地理解粘弹性流体的流动行为。
控制方程组的方程类型是理解粘弹性流体流动的关键所在,随着对粘弹性流体流动的进一步探究,相信将能够更好地控制和利用粘弹性流体的流动现象,为科学领域带来更广阔的前景。