话说,苏格兰爱丁堡的默奇斯顿塔楼是一座方形建筑,古老的石块上布满了岁月的痕迹,几扇狭长而深邃的窗户不规则地镶嵌其上,仿佛在诉说着它的历史。

默奇斯顿城堡,爱丁堡 1454 build | 图源wikipedia
塔楼的锯齿形屋顶犹如一顶王冠,使得它在岁月的侵蚀下依然显得高贵而自豪。
早在1550年,约翰·纳皮尔(John Napier)就出生在这座墨奇斯顿城堡中。
后来,他的名字不仅被冠在了这所大学上,还因为一种彻底改变了科学的数学运算而闻名于世。

约翰·纳皮尔
约翰·纳皮尔是个奇人,你必须记住他,因为他的兴趣涉猎广泛,从神学到天文学,再到数学。
坊间流传着一个关于他的逸事,虽然与数学无关,却能让我们窥见他的独特性格。
纳皮尔的邻居罗斯林(Roslin)养的鸽子经常飞到他的院子里吃谷粒。纳皮尔非常生气,警告邻居如果不管住这些鸽子,他就要把它们没收了。
邻居对此不以为然,叫纳皮尔尽管去抓。
第二天早上,纳皮尔手持一个大袋子,轻松捉住了所有的鸽子——原来,他在自家院子里撒满了浸泡过白兰地的谷粒,鸽子们吃得酩酊大醉,毫无抵抗之力。
这个故事或许只是传闻,但它告诉我们,纳皮尔善于用出其不意的方法解决问题。
有时候,只需改变视角,就能找到解决办法。
纳皮尔将这种创新思维应用到了数学上,发明了一种革命性的运算方法,使乘法变得如同加法般简单。

他发明了对数,将乘法和加法巧妙地联系起来。
通过把乘法轴和加法轴平行放置,纳皮尔创造了一个数学奇迹。
在乘法轴上,每个刻度对应前一个刻度乘以2;而在加法轴上,每个刻度对应前一个刻度加1。
这样,通过简单的图表,从加法到乘法的转换瞬间变得可能。
例如,如果你想计算8×16,纳皮尔的方法是这样的:
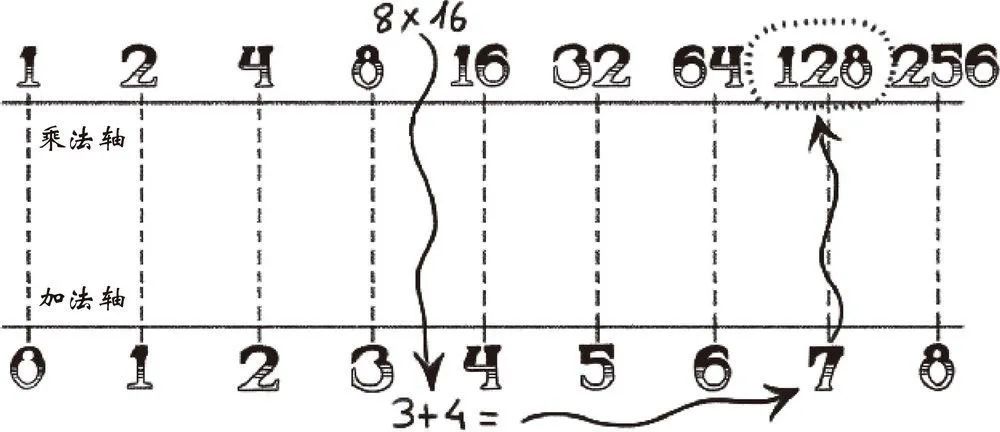
在加法的世界里,8×16变成了3+4;
计算3+4=7;
再把结果带回乘法世界,7变成了128。
你得到的结果是8×16=128。
再比如:
假设我们有两个数,2 和 8。你知道 2×8=16,对吧?
我们可以使用对数来简化这个计算。
首先,我们找到 2 和 8 的对数,是 1 和 3。然后,我们把这两个对数相加:1 + 3 = 4。
最后,我们把结果 4 转换回去,就得到了 16。”
这种转换看似魔术,但效果确实很好。
这种方法不仅适用于简单的数,还可以用于更复杂的乘法运算。
假设你需要计算2.43×78.35,有一本加法/乘法对照表,查找数值后,将乘法2.43×78.35变成加法1.281+6.292,几秒钟内算出和7.573,再将结果带回乘法中,得到约190.4的结果。
如此,你在不到30秒内完成了复杂的乘法运算。
你可能会问,这人是不是没事干,为啥发明一个这个东西呢?
其实和当时的背景有关,正好当年著名的天文学家开普勒。他每天都在计算行星的运动轨迹,这些计算涉及到非常大的数字,乘法和除法让他头疼不已。
开普勒总是抱怨:“如果有一种方法能让我不必做这么多复杂的计算就好了!”
就在开普勒为计算苦恼的时候,数学家约翰·纳皮尔(John Napier)正在思考一个问题:“有没有一种方法能将乘法和除法变得像加法和减法一样简单呢?”
纳皮尔经过多年的研究,终于发明了对数表。
纳皮尔花了二十多年才发展出这一理论并制作出加法/乘法表,所有计算都是手工完成的。
1614年,他发表了《奇妙的对数表的描述》(Mirifici logarithmorum canonis descriptio),并首次使用“对数”这个词,来描述乘法和加法之间的桥梁。
对数表详细罗列了5400个数,通过查找这些数,可以在几秒钟内完成复杂的乘法计算。

对数表
虽然对数表的结果只是近似值,但对于当时的科学计算来说已经足够精确。
对于更复杂的乘法,只需知道1到1000的对数,通过抛弃零和小数点进行计算,就能快速得出结果。
纳皮尔的对数表极大地提高了计算效率,使得科学家们能将一整天的工作压缩到几小时内完成。
随着时间推移,更多数学家发布了更精确的对数表,这些对数表迅速传播,成为科学家、建筑师、会计师等的主要工具。
直到20世纪下半叶,计算机的出现才逐渐取代了对数表的地位。
但对数这一概念依然在科学中扮演重要角色,从地震强度的里氏震级到声音强度的分贝,再到溶液酸度的pH值和恒星的亮度等,都使用了对数标度。
例如,里氏震级中,每增加一度代表现实中振幅增加10倍,因此7级地震的振幅比6级地震大10倍。

而人类记录到的最强烈的地震,1960年智利瓦尔迪维亚地震,震级9.5,其振幅比普通的3.5级地震大一百万倍。
另一个例子是音阶,音符的特征是其振动频率。
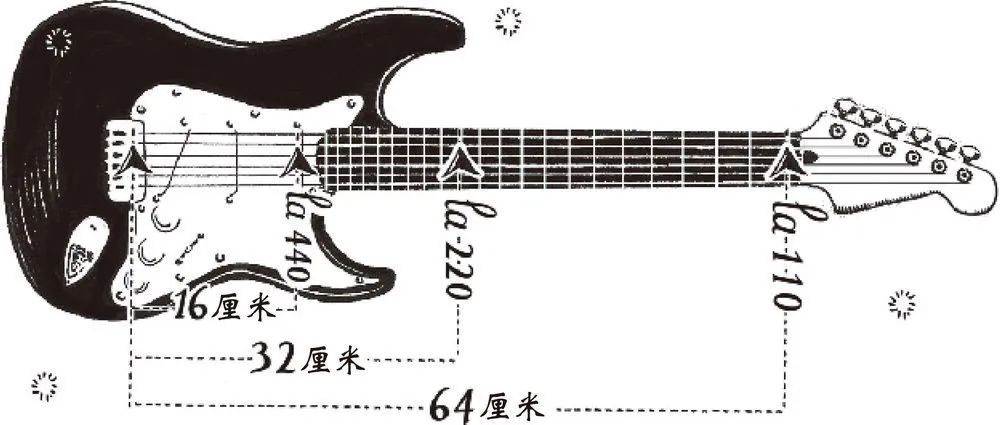
钢琴键上的音符从低到高依次是55Hz、110Hz、220Hz、440Hz、880Hz、1760Hz和3520Hz,每两个音符相隔一个八度音程,高音符的振动频率是低音符的两倍。
吉他琴颈上的品位也按此排列,离琴头越近,音差越大。
在同一根弦上,低音la的品位与琴桥的距离是高音la的两倍。
另外,我们再补充下:
约翰·纳皮尔最初发明的对数并不是基于我们今天常用的底数(例如10或e)。
他发明的对数是一种特殊的形式,被称为“纳皮尔对数”,其底数实际上与现代常用的自然对数(底数为e)有一些关系。
具体来说,纳皮尔的对数是基于一个递减的指数函数,但它并没有明确规定一个底数。
纳皮尔的对数是以一种复杂的方式定义的,并且他的计算方法与我们今天使用的对数表略有不同。
后来,英国数学家亨利·布里格斯(Henry Briggs)在1617年引入了以10为底的常用对数(常用对数,或布里格斯对数),这才使得对数的概念更易于理解和应用。
为了简单理解,可以这样描述:
纳皮尔对数:纳皮尔自己发明的对数,并没有一个明确的底数,主要用于简化复杂的乘法和除法计算。
常用对数(以10为底):由亨利·布里格斯引入,使对数的应用更加广泛。
自然对数(以e为底):后来由数学家们发展出,以自然常数e(约2.718)为底数的对数。
所以,纳皮尔最初发明的对数并没有一个明确的底数,更多是一种数学工具和方法的创新,而非我们今天使用的具体底数对数。
但,无论如何,所有的一切都有一个数学表达式:
(1)通用对数公式:

(2)常用对数公式:

(3)自然对数(e为底):

总结:
约翰·纳皮尔的对数理论不仅是数学史上的里程碑,其影响深远。
尽管现代计算技术的发展已使对数表不再是主要工具,但对数这一概念依然广泛应用于科学和日常生活中。
而且我们也不能忘记这个已经被销声匿迹的工具,毕竟曾经创造过辉煌,他就和我们小时候用的磁带(以前的录音机用的)只是短暂而逝。
纳皮尔用他那独特的视角和创新思维,为后世架起了一座从乘法世界到加法世界的桥梁,使得许多复杂的问题变得简单易解。
对数不仅在数学领域焕发新生,还在众多物理现象的测量中发挥着重要作用。