根据三角形三边长关系，添加辅助线构造三角形，介绍已知三角形边长a=1,b=2，求下图中线CD取值范围的主要步骤。

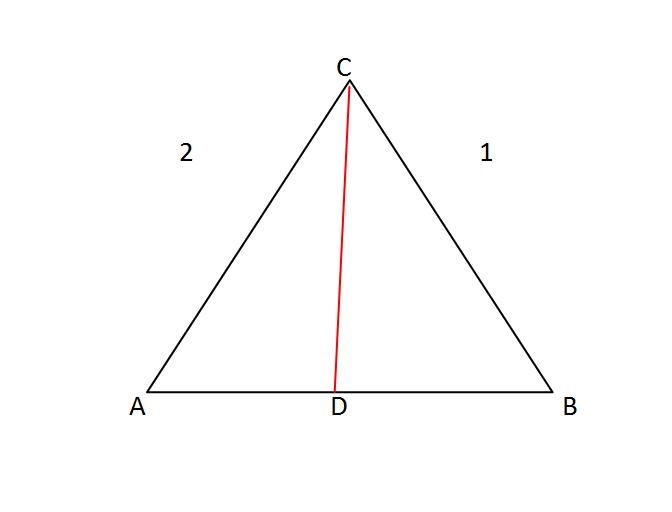
思路：三角形任意两边长的和大于第三边长，任意两边长的差小于第三边。

解：对于本题，所求的是中线CD的取值范围，已知的是AC和BC的长，所以需要构造三角形将所求问题与已知条件建立联系。

延长CD到E点，使得DE=CD，链接AE，

在△CBD和△ADE中，有：

CD=DE,

∠CDB=∠ADE,

AD=DB,

所以△CBD≌△ADE，

则：AE=BC=1。

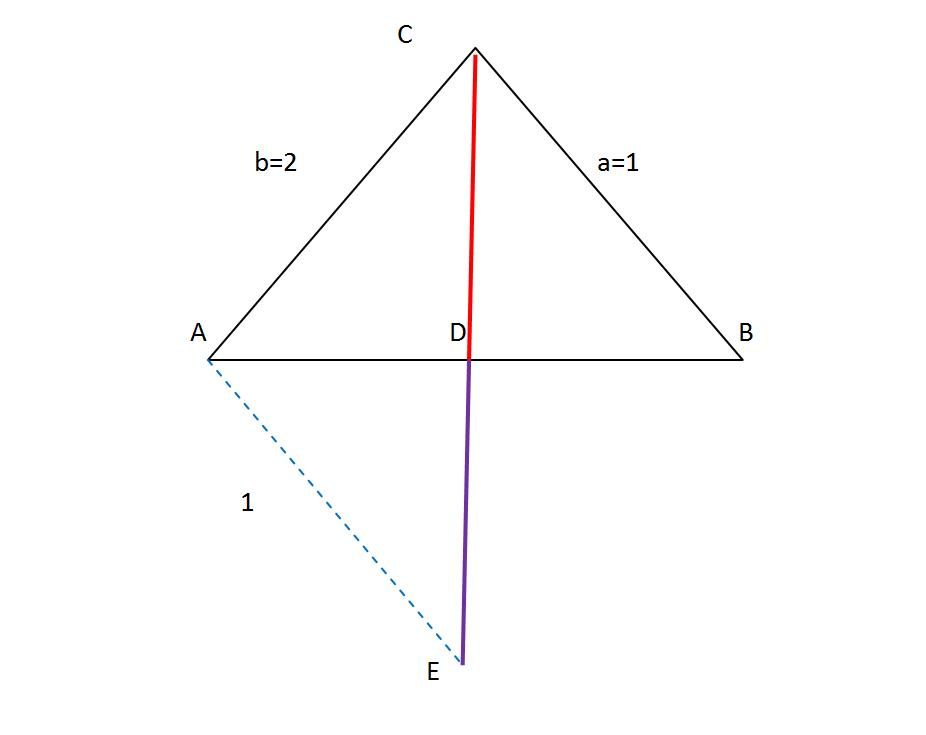
在三角形AEC中，根据三角形两边的长度和大于第三边长度有：

AC+AE＞CE，即：

2+1＞2CD,

所以：CD<3/2；

再由三角形两边长度的差小于第三边则有：

AE＞|1-2|=1，即：

2CD＞1，

所以：CD＞1/2，

综上可知，1/2＜CD＜3/2。