比如,如果你有6块糖果,把它们分给2个朋友,每个人自然会得到3块。所以我们很容易接受像6除以2等于3这样的简单数学运算。
然而,当我们尝试将除数变为零时,事情就变得复杂起来。
为什么不能除以零?
为什么中学老师和数学家说“除以零未定义”?我们曾经究竟有没有思考这里面的真实原因是什么?
其实,这背后的原因其实深藏着数学的神秘和复杂性,涉及几个世纪以来数学家们的深入思考和研究。
01 什么是除法?
为了理解为什么不能除以零,首先我们需要明确除法的本质。
简单来说,除法的本质是乘法的逆运算。
当我们说6除以2等于3时,实际上是在说2乘以3等于6。这个关系建立在乘法的基础之上,它适用于任何两个非零的数字。
现在,我们来思考一下除以零的情况。假设我们想计算A除以0(即A/0)。
如果我们套用乘法的逆运算定义,这实际上是在寻找一个数字c,使得0乘以c等于A。换句话说,我们想找到一个数字c,使得:

但是这里出现了一个重大问题。任何数字乘以0的结果都是0,也就是说,无论c是什么,0乘以它的结果都永远是0。
因此,除非A也是0,否则我们根本无法找到一个符合条件的数字c。这就导致了除以零的问题——它没有意义!
02 0除以0的问题
好吧,假设A等于0,情况又会如何呢?
让我们看看0/0会得到什么。根据前面的逻辑,0/0 = c的意思是0乘以c等于0。这看起来似乎是可以接受的,因为无论c是什么,0乘以c都会等于0。
但问题在于,这个等式对“任何c值”都成立,也就是说,0/0可以是任何数字。这就让结果变得不明确了,因为我们无法确定0/0到底应该等于什么。
如果0/0可以是任意数字,那么数学的其他部分也会陷入混乱。这种不明确性就是为什么0除以0同样是未定义的原因。
既然除以零会导致问题,那为什么不简单地为它定义一个特殊的值呢?
事实上,历史上有数学家提出过这样的想法,但这在数学结构中引发了更大的麻烦。
我们依赖于某些数学规则和性质来确保数学的稳定性和一致性。一个重要的原则是“乘法的恒等式”:对于任何数字a,都有a乘以1等于a。
如果我们定义了除以零的值,这些基本性质就可能会失效,导致数学体系的崩溃。
例如,假设我们定义了1/0等于某个特殊的数X。那么根据除法的逆运算原则,这意味着:
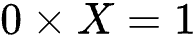
但我们已经知道,0乘以任何数的结果只能是0,绝不可能等于1。
这种逻辑上的矛盾让除以零的运算无法合理定义。因此,数学家最终决定,将除以零视为未定义操作,以确保数学规则的自洽性。
03 微积分的极限思维:逼近零
虽然直接除以零是未定义的,但这并不意味着我们无法探讨与“零”相关的数学现象。
微积分提供了一种方法,通过「极限」的概念,帮助我们理解当数字接近零时会发生什么。极限允许我们研究当某个值逐渐趋近于零时,某些函数的行为。
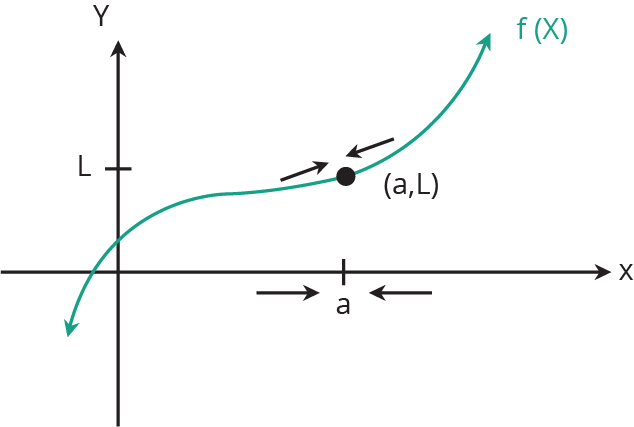
举个例子,考虑函数f(x) = 1/x。当你试图计算f(0)时,很快就会意识到1/0是未定义的。但通过观察x接近0时的情况,我们可以发现一些有趣的现象。
当x逐渐趋向于正的零(从正数方向接近0),f(x)的值会越来越大,趋向于正无穷大;

而当x逐渐趋向于负的零(从负数方向接近0),f(x)的值则会越来越小,趋向于负无穷大。

这意味着,没有一个明确的值可以表示f(0),因为从两个不同方向接近零,结果是完全不同的。
这种情况表明,除以零之所以无法定义的一个重要原因,就是它的行为在不同方向上不一致。
在一个方向上结果趋向于正无穷大,而在另一个方向上结果却趋向于负无穷大。这种根本的不一致性正是为什么我们无法给出除以零一个明确的数值。
04 0/0和不确定形式
在微积分中,除以零引发的另一类问题是所谓的“不确定形式”,其中最著名的形式之一就是0/0。
比如,当我们面对一个表达式,其分子和分母都趋向于零时,无法直接得出结论。
这时候,微积分提供了一种强大的工具——L’Hopital法则(洛必达法则),帮助我们求解这些极限。

L’Hopital法则的基本思路是,如果一个函数的分子和分母都趋近于零(或无穷大),我们可以通过求分子和分母的「导数」来计算极限。
例如,对于函数f(x) = (sin(x))/x,当x趋近于零时,分子和分母都趋向于零,但通过求导,我们可以得出这个函数的极限为1。
这种方法不仅帮助我们解决了很多实际问题,也让我们对除以零的现象有了更深层次的理解。
虽然0/0无法直接计算,但通过极限方法,我们可以找到其近似的行为,从而避免“未定义”的尴尬局面。
为什么我们如此严格地禁止除以零?
原因很简单:数学是一门精确的科学,它依赖于一致的规则和逻辑。
如果我们允许除以零这样的操作,整个数学体系可能会陷入混乱。试想一下,如果0/0可以是任意值,那么数学中的许多公式、定理将失去其精确性,甚至失去意义。
此外,除以零的问题不仅限于数学理论,它还对许多实际应用有重要影响。
例如,在物理学中,某些计算可能涉及极限值的逼近或某些“趋近于零”的情况。如果这些操作处理不当,可能会导致模型崩溃或者错误的结论。
总结
除以零看似简单,但其背后隐藏着复杂的数学原理。
它不仅打破了乘法的基本原则,还可能导致数学中的各种不一致。正因为如此,数学家选择将除以零视为未定义的操作。
尽管如此,微积分中的极限方法为我们提供了一种理解和处理“接近零”的问题的方法,帮助我们在更广泛的数学领域中探讨这些问题。