我一直在思索如何定位AI与日常数学建模教学的关系。毋庸置疑,AI很强大,甚至很多内容上的回答很“靠谱”。但如果学生依赖它进行问题解决和作业完成,极有可能“不过脑子”,最后形成不了真正的思维能力。可转念一想,AI已经是当下社会的重要工具,学会合理利用它也是教育应有之义。
思索了很久之后,我似乎找到了一个重要的突破口,那就是:先搞清楚学生到底应该学些什么知识?
如果搞清楚了上述问题,并且清楚AI可以在哪些知识上起作用,我们就有思路定位AI与教学之间的关系了。
有两类知识非常重要,但在我们平时的语境中很少提到,那就是“驱动性知识”和“哲学性知识”。这些概念来自于朱浩楠老师的《为什么是数学》一书。不过要讲清楚这个概念,我们得先介绍一下对应的知识分类。
《为什么是数学》中提出了五种知识类型:事实性知识、操作性知识、原理性知识、驱动性知识和哲学性知识。这些知识类型各有特点,在数学建模教学中有着不同的作用。下面是我根据书中叙述做的简单总结:
事实性知识
定义:“知道是什么”的知识。示例:数学定义、定理、数据、规则、行业规范等。作用:为建模提供基础材料,但仅靠这些无法深入问题本质。操作性知识
定义:“知道做的步骤”的知识。示例:算法实现、建模流程、计算器或软件的使用。作用:确保模型建立的技术可行性,帮助完成具体任务。原理性知识
定义:“知道为什么是”的知识。示例:学科思想、理论和观念。作用:支持知识迁移和问题的深度解决,是创新的基础。驱动性知识
定义:“知道为什么不是”的知识。示例:通过试错与反思发现问题、优化模型的能力。作用:推动学生突破既有框架,发现新思路,是创新工作的核心。哲学性知识
定义:“知道为什么存在”的知识。示例:对知识意义的探索、对模型本质的思考。作用:激发学生的学习动力和对问题的更深层次理解。本人和朱浩楠老师认识多年,朱老师在数学建模哲学和方法论上有非常多精彩的论述给了我很多启发。下图是朱老师的关于上述5类知识的讲座截图:

其实看到这个分类框架,已经能给人很多启发了!就比如我,当第一次听到关于“驱动性知识”和“哲学性知识”的时候就恍然大悟,为什么有的学生看起来学了很多内容、花了很多时间,但却总让我感觉“没学到本质”,实则是学生缺乏上述两类知识。
在教学中,如何平衡这五类知识的教学,尤其是驱动性知识和哲学性知识的培养,是一个值得深思的问题。这两类知识在传统教学中容易被忽视,但它们对于培养学生的创造力和批判性思维尤为重要。
驱动性知识需要通过试错和实践积累,无法通过单纯的讲授传递。这类知识帮助学生在建模中发现假设的不足、模型的缺陷并提出改进方案。
哲学性知识关注知识的意义和价值,激发学生对问题的深刻思考。可以帮助学生认识到建模的社会意义、人文价值以及背后的深层逻辑。
我尝试画一幅图,表达我对上述5类知识的理解:
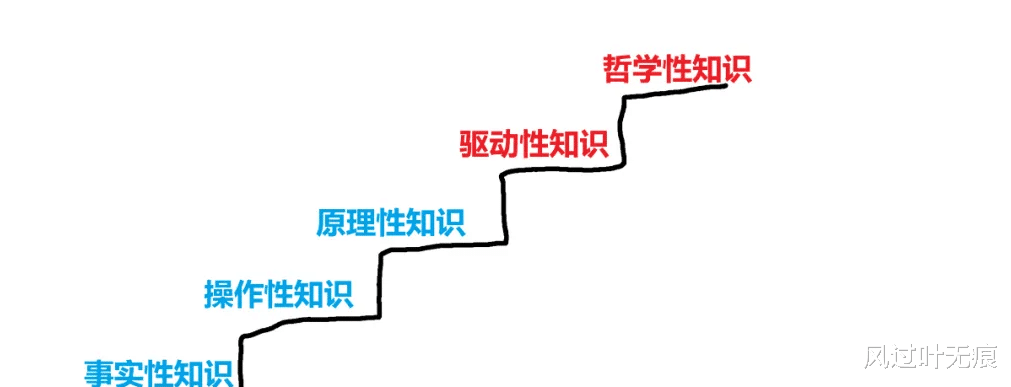
上述知识是逐层递进的,从事实性知识不断向上延展和推进,但不能只停留在事实性和操作性知识上,驱动性知识彰显独立思考和批判精神,哲学性知识则给出更为根本的思考。
我尝试再画一幅图,如果学生只有大量的前三类知识,那么他/她的知识结构是这样的:

前三类知识AI非常擅长,只要给AI一个指示,它可以唰唰唰地给你输出,因为无非是提取记忆嘛。但是后两类AI很难替代,就像你可以问导航软件,从A到B该怎么走,但是为什么要去B而不是去C,对路线意义的发问,这是AI很难替代的。
如果让我为一个学生的创新思维素养打分的话,可以建立一个简单的模型:
定义创新素养为驱动性知识和哲学性知识在总知识中的占比动学驱动哲学
是驱动性和哲学性知识的分值,总
是总知识量。高创新素养的学生驱动性和哲学性知识占比高。低创新素养的学生知识结构偏向基础层次,创新能力较弱。
AI在教学中能很好地处理前三类知识(事实性、操作性和原理性知识),但在驱动性知识和哲学性知识上存在局限性。
AI的优势在于提供:
事实性知识:快速检索、提供答案。操作性知识:自动化计算、算法实现。原理性知识:辅助理解复杂模型。AI的局限在于:
驱动性知识:AI无法进行真正的试错与反思,只能提供工具和支持。哲学性知识:AI无法理解模型的意义和价值,难以帮助学生深入思考“为什么”。简而言之,AI可以很好地解决前三类知识的问题,但后两类知识需要学生主动探索。数学建模教学的目标,是在学生掌握基础知识的同时,培养他们的创新能力和独立思考。通过引入驱动性知识和哲学性知识:帮助学生主动发现问题、解决问题。激发学生思考模型的意义和价值。
悟了悟了!
《为什么是数学:关于数学建模、认知和科学思想的30次对话》是朱浩楠老师的又一力作。利用数学建模方法讨论了人类社会和自然界中的33个话题,不仅解答了大众对于数学的最常见疑问:“数学有什么用?”更是以高中知识为主要工具、以数学建模为主要载体、以中学生能够理解的方式,展现了数学研究的基本过程和思维方式。