对于存在权重为负的环路的有向图,我们可以使用 Bellman-Ford 算法的一个变种来检测并列出该环路上的所有节点。Bellman-Ford 算法通常用于检测图中是否存在负权重的环路,并可以找出从源点到所有其他节点的最短路径(如果存在负权重环路,则不存在最短路径)。为了找出环路上的所有节点,我们可以稍微修改算法的执行过程。
算法思路1. 初始化:对图中的每个节点 v,设置其最短路径估计 dist[v] = +∞(除了源点 s,设置 dist[s] = 0)。2. 松弛操作:对所有边 (u, v) 重复进行松弛操作 n-1 次(其中 n 是节点数量),尝试通过边 (u, v) 更新 dist[v]。如果某次更新后 dist[v] 减小了,则标记边 (u, v)。3. 检测负权重环路:再进行一次遍历所有边的松弛操作,但不更新 dist 数组。如果在此过程中发现任何 dist[v] 还能被进一步减小,那么图中存在负权重环路。此时,我们可以从这条边 (u, v) 开始回溯,通过之前标记的边来找到整个环路。4. 回溯环路:由于我们在第2步中标记了可能导致负权重环路的边,我们可以从这些边开始回溯,直到形成一个环路。Go 语言实现以下是一个简化的 Go 语言实现,重点在于检测并列出负权重环路中的节点:
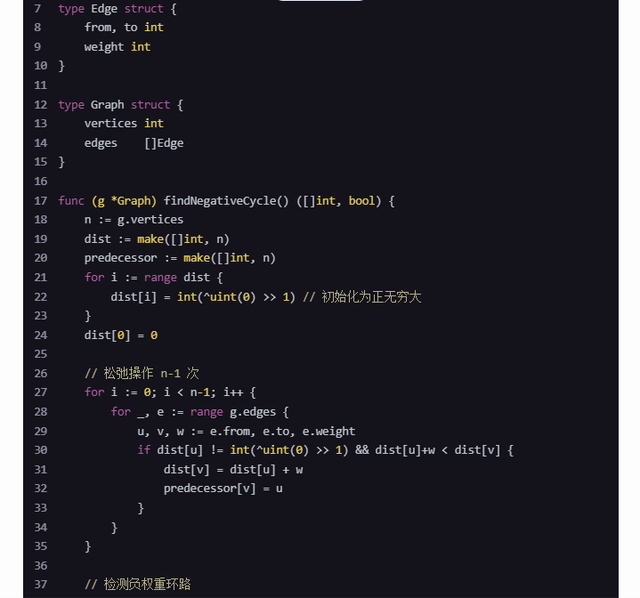
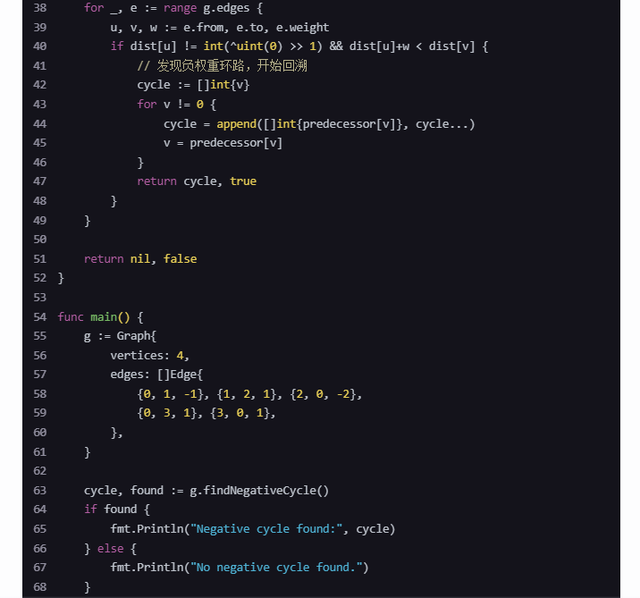
package mainimport("fmt")typeEdgestruct{from, to int weight int}typeGraphstruct{ vertices int edges []Edge}func (g *Graph) findNegativeCycle()([]int,bool){ n := g.vertices dist :=make([]int, n) predecessor :=make([]int, n)for i :=range dist { dist[i]=int(^uint(0)>>1)// 初始化为正无穷大} dist[0]=0// 松弛操作 n-1 次for i :=0; i < n-1; i++{for _, e :=range g.edges { u, v, w := e.from, e.to, e.weightif dist[u]!=int(^uint(0)>>1)&& dist[u]+w < dist[v]{ dist[v]= dist[u]+ w predecessor[v]= u}}}// 检测负权重环路for _, e :=range g.edges { u, v, w := e.from, e.to, e.weightif dist[u]!=int(^uint(0)>>1)&& dist[u]+w < dist[v]{// 发现负权重环路,开始回溯 cycle :=[]int{v}for v !=0{ cycle =append([]int{predecessor[v]}, cycle...) v = predecessor[v]}return cycle,true}}returnnil,false}func main(){ g :=Graph{ vertices:4, edges:[]Edge{{0,1,-1},{1,2,1},{2,0,-2},{0,3,1},{3,0,1},},} cycle, found := g.findNegativeCycle()if found { fmt.Println("Negative cycle found:", cycle)}else{ fmt.Println("No negative cycle found.")}}注意• 这个代码片段假设图是连通的,并且源点是顶点 0。• 在实际应用中,可能需要更复杂的逻辑来处理非连通图或选择多个源点。• 回溯时,我们假设环路至少包含一个非零节点,且环路以 0 开始(如果环不包含 0,则需要从另一个点开始回溯,或者通过额外的逻辑找到环的起始点)。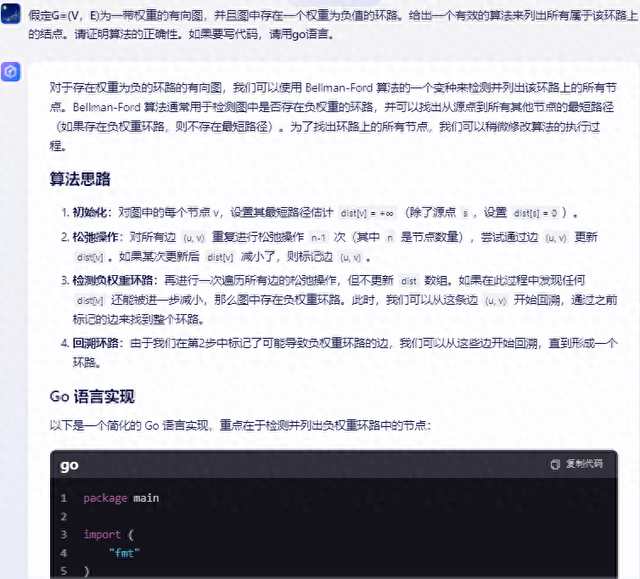
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
讯飞星火:首先,我们需要理解这个问题。给定一个带权重的有向图G=(V, E),其中存在一个权重为负值的环路,我们需要找出这个环路上的所有节点。
为了解决这个问题,我们可以使用贝尔曼-福特算法(Bellman-Ford algorithm)。该算法可以检测图中是否存在负权重环路,并找到环路中的节点。以下是算法的基本步骤:
1. 初始化所有顶点的距离值为无穷大,除了起始顶点的距离值为0。2. 对于每个顶点,重复以下操作 |V| - 1 次(|V|表示顶点的数量): a. 遍历所有的边 (u, v),如果从起点到顶点 u 的距离加上边的权重小于从起点到顶点 v 的距离,则更新顶点 v 的距离。3. 再次遍历所有的边 (u, v),如果从起点到顶点 u 的距离加上边的权重小于从起点到顶点 v 的距离,则存在负权重环路。4. 如果存在负权重环路,我们可以通过回溯的方式找到环路中的所有节点。下面是用Go语言实现的贝尔曼-福特算法:
package mainimport("fmt""math")typeEdgestruct{from, to, weight int}func BellmanFord(edges []Edge, numVertices, startVertex int)([]int,bool){ distance :=make([]float64, numVertices)for i :=range distance { distance[i]= math.Inf(1)} distance[startVertex]=0for i :=0; i < numVertices-1; i++{for _, edge :=range edges {if distance[edge.from]+float64(edge.weight)< distance[edge.to]{ distance[edge.to]= distance[edge.from]+float64(edge.weight)}}}for _, edge :=range edges {if distance[edge.from]+float64(edge.weight)< distance[edge.to]{returnnil,true// Negative cycle detected}}return distance,false}func main(){ edges :=[]Edge{{0,1,5},{0,2,4},{1,3,3},{2,1,-6},{3,2,2},} numVertices :=4 startVertex :=0 distance, hasNegativeCycle :=BellmanFord(edges, numVertices, startVertex)if hasNegativeCycle { fmt.Println("Negative cycle detected")}else{ fmt.Println("Distances:", distance)}}注意:这个代码只检测了是否存在负权重环路,但没有列出环路中的节点。要找到环路中的节点,需要在检测到负权重环路后,使用额外的数据结构(如队列)来跟踪路径,并在每次迭代时检查是否有更短的路径。
360智脑:要找出带权有向图中所有属于权重为负值的环路的节点,我们可以使用Bellman-Ford算法的一个变种。Bellman-Ford算法可以用来检测图中是否存在负权重环路,并且在存在负权重环路的情况下,它能够指出哪些节点参与了这个环路。
以下是一个使用Go语言实现的算法:
package mainimport("fmt")typeEdgestruct{from, to int weight int}func findNegativeCycle(edges []Edge, numVertices int)([]int,bool){// Initialize distances distances :=make([]int, numVertices)for i :=range distances { distances[i]=1<<31-1// Set to infinity} distances[0]=0// Start node has distance 0// Relax edges repeatedlyfor i :=0; i < numVertices; i++{for _, edge :=range edges {if distances[edge.from]+edge.weight < distances[edge.to]{ distances[edge.to]= distances[edge.from]+ edge.weightif i == numVertices-1{// We found a negative cyclereturn getCycleNodes(edges, edge),true}}}}returnnil,false}func getCycleNodes(edges []Edge, lastEdge Edge)[]int{// Find the nodes in the negative cycle cycleNodes :=[]int{lastEdge.to} currentNode := lastEdge.fromfor currentNode != lastEdge.to {for _, edge :=range edges {if edge.to == currentNode && distances[edge.from]+edge.weight == distances[edge.to]{ cycleNodes =append([]int{edge.from}, cycleNodes...) currentNode = edge.frombreak}}}return cycleNodes}func main(){ edges :=[]Edge{{0,1,1},{1,2,-2},{2,0,1},} numVertices :=3 cycleNodes, found := findNegativeCycle(edges, numVertices)if found { fmt.Println("Negative weight cycle nodes:", cycleNodes)}else{ fmt.Println("No negative weight cycle found.")}}这个算法首先初始化所有节点的距离为无穷大,除了起始节点。然后,它对所有的边进行numVertices次松弛操作。如果在第numVertices次松弛操作中仍然有边可以被松弛,那么就意味着图中存在一个负权重环路。在这种情况下,我们通过回溯找到所有参与负权重环路的节点。
算法的正确性可以通过Bellman-Ford算法的原理来证明。在进行了numVertices次松弛操作后,如果还有边可以被松弛,那么就说明存在一个负权重环路,因为在一个没有负权重环路的图中,最多只需要numVertices - 1次松弛操作就可以得到最短路径。通过记录最后一次松弛操作的边,并沿着这些边的反方向回溯,我们可以找到所有参与负权重环路的节点。
智谱清言:为了找到带权重的有向图中的负权重环路,我们可以使用贝尔曼-福特算法(Bellman-Ford algorithm)的变种。以下是算法的步骤: 算法步骤:
1. 初始化:选择一个顶点作为源点,将其距离设置为0,其他所有顶点的距离设置为无穷大。2. 松弛操作:对于图中的每一条边,如果通过该边可以使得终点的距离变小,则更新终点的距离和前驱节点。3. 检测负权重环路:在完成松弛操作V-1次之后(V是顶点的数量),再次进行一轮松弛操作。如果在这一轮中,仍然有顶点的距离被更新,则图中存在负权重环路。4. 找到环路:如果检测到负权重环路,从被更新的顶点开始,通过前驱节点回溯,直到形成一个环路。 以下是Go语言的实现:package mainimport("fmt")typeEdgestruct{fromintto intweight int}func findNegativeCycle(graph [][]Edge, V int)[][]int{dist :=make([]int, V)prev :=make([]int, V)for i :=range dist {dist[i]=int(1e9)}dist[0]=0// 松弛操作,执行V-1次for i :=0; i < V-1; i++{for j :=0; j < V; j++{for _, edge :=range graph[j]{if dist[edge.to]> dist[j]+edge.weight {dist[edge.to]= dist[j]+ edge.weightprev[edge.to]= j}}}}// 检测负权重环路for j :=0; j < V; j++{for _, edge :=range graph[j]{if dist[edge.to]> dist[j]+edge.weight {return findCycle(prev, edge.to)}}}returnnil}func findCycle(prev []int, start int)[][]int{var cycle [][]intnode := startfor{cycle =append([][]int{{node, prev[node]}}, cycle...)if prev[node]== start {break}node = prev[node]}return cycle}func main(){V :=5graph :=make([][]Edge, V)graph[0]=append(graph[0],Edge{0,1,-1})graph[1]=append(graph[1],Edge{1,2,-2})graph[2]=append(graph[2],Edge{2,3,-3})graph[3]=append(graph[3],Edge{3,4,-4})graph[4]=append(graph[4],Edge{4,1,5})cycles := findNegativeCycle(graph, V)if cycles !=nil{fmt.Println("Negative weight cycle exists:")for _, cycle :=range cycles {fmt.Printf("%d -> %d\n", cycle[0], cycle[1])}}else{fmt.Println("No negative weight cycle exists.")}}算法正确性证明:5. 贝尔曼-福特算法在V-1次迭代后,可以找到从源点到所有顶点的最短路径。6. 如果在V次迭代后,仍然可以更新某个顶点的距离,说明存在一条路径,使得经过这条路径回到该顶点的总权重小于0,即存在负权重环路。7. 通过前驱节点数组,我们可以从环路中的某个顶点开始,回溯到源点,形成一个环路。8. 该算法可以检测并找到所有的负权重环路,因为它考虑了所有可能的边。 注意:这个算法的时间复杂度是O(V*E),其中V是顶点数,E是边数。在实际情况中,如果图非常大,这个算法可能会非常慢。天工:算法描述:Bellman-Ford 算法检测负权重环算法步骤:1. 初始化距离:• 对于图 G = (V, E),初始化所有顶点到源点 s 的距离为无穷大,除了源点自身距离为 0。2. 松弛操作:• 如果 dist[v] > dist[u] + weight(u, v),则更新 dist[v] = dist[u] + weight(u, v),同时记录下 v 的前驱节点为 u。• 对于每条边 (u, v) ∈ E,执行松弛操作:• 重复此过程 V-1 次,其中 V 是顶点的数量。3. 检测负权重环:• 如果 dist[v] > dist[u] + weight(u, v) 仍然成立,则存在负权重环。• 再次执行松弛操作:4. 提取负权重环:• 从任意一个在第 V 次迭代中更新的节点开始,通过前驱节点回溯,直到再次遇到该节点,即可得到负权重环。证明算法正确性• 正确性:• 在 V-1 次迭代后,所有最短路径(不包含负权重环)都已经被正确计算。• 第 V 次迭代中,如果存在更新,则表明存在一条更短的路径,这只能通过包含负权重环来实现。• 检测负权重环:• 如果存在负权重环,它将被检测到,因为任何经过负权重环的路径在第 V 次迭代时都会得到进一步的缩短。Go 语言代码实现package mainimport("fmt")typeEdgestruct{from, to int weight int}func detectNegativeWeightCycle(edges []Edge, V int)[]int{ dist :=make([]int, V) prev :=make([]int, V)for i :=range dist { dist[i]=10000// Use a large number to represent infinity prev[i]=-1} dist[0]=0for i :=0; i < V; i++{for _, edge :=range edges { u, v, w := edge.from, edge.to, edge.weightif dist[u]!=10000&& dist[u]+w < dist[v]{ dist[v]= dist[u]+ w prev[v]= uif i == V-1{// Detect a negative weight cycle v = findNegativeCycle(edges, prev, v)if v !=-1{ fmt.Println("Negative weight cycle found:") printCycle(prev, v)returnnil// Return nil to indicate cycle found}}}}}return dist}func findNegativeCycle(edges []Edge, prev []int, v int)int{for _, edge :=range edges {if edge.to == v && prev[v]== edge.from&& dist[v]> dist[edge.from]+ edge.weight {return v}}return-1}func printCycle(prev []int, v int){ cycle :=[]int{v}for prev[v]!= v { v = prev[v] cycle =append([]int{v}, cycle...)} fmt.Println(cycle)}func main(){ edges :=[]Edge{{0,1,1},{0,2,4},{1,2,-3},{2,3,2},{3,1,-2},} V :=4 detectNegativeWeightCycle(edges, V)}请注意,上述代码示例中,detectNegativeWeightCycle 函数检测负权重环,findNegativeCycle 和 printCycle 分别用于确认和打印负权重环。在 main 函数中定义了图的边,其中包含一个负权重环。
chatgpt:要找出带有负权重环路的图中所有结点,可以使用 Bellman-Ford 算法。该算法可以检测图中是否存在负权重环路,并且可以列出这些环路上的所有节点。
以下是该算法的步骤:
1. 初始化一个数组用于存储到每个节点的最短距离和前驱节点。2. 重复 |V|-1 次(V为节点数)以下步骤: a. 遍历所有的边,更新每条边的两个节点的最短距离。3. 再次遍历所有的边,如果仍然存在一条边的两个节点满足 dist[v] > dist[u] + weight(u, v),则说明存在负权重环路。接下来是带有负权重环路的结点示例代码,使用Go语言实现:
package mainimport"fmt"// 边结构体typeEdgestruct{ src, dest, weight int}func printNegativeWeightCycle(edges []Edge, dist []int, V, E int){for _, edge :=range edges { u := edge.src v := edge.dest weight := edge.weightif dist[u]!=int(^uint(0)>>1)&& dist[v]> dist[u]+weight { fmt.Printf("节点 %d 在负权重环路中\n", v)}}}func bellmanFord(graph []Edge, V, E, src int){ dist :=make([]int, V)for i :=0; i < V; i++{ dist[i]=int(^uint(0)>>1)} dist[src]=0for i :=1; i <= V-1; i++{for j :=0; j < E; j++{ u := graph[j].src v := graph[j].dest weight := graph[j].weightif dist[u]!=int(^uint(0)>>1)&& dist[v]> dist[u]+weight { dist[v]= dist[u]+ weight}}} printNegativeWeightCycle(graph, dist, V, E)}func main(){ graph :=[]Edge{{0,1,4},{1,2,-1},{2,3,-2},{3,1,3},} V, E :=4,len(graph) src :=0// 从节点0开始 bellmanFord(graph, V, E, src)}这段代码用于检测图中是否存在负权重环路,并打印出负权重环路上的所有结点。可以根据实际的图结构和节点权重进行适当的修改。Bellman-Ford算法可以保证找到带负权重环路的所有结点。
kimi:要解决这个问题,我们可以使用贝尔曼-福特算法(Bellman-Ford algorithm),该算法能够找出图中的负权环。算法的基本思想是,对于每个顶点,尝试通过其他所有顶点进行松弛操作,如果经过多次迭代后,权重还能继续降低,则说明存在负权环。
算法步骤:1. 初始化:将所有顶点的最短路径值初始化为无穷大,除了源点(可以是任意一个顶点),其最短路径值初始化为0。2. 松弛操作:对于图中的每一条边,尝试更新其邻接点的最短路径值。如果通过当前边到达邻接点的路径值小于当前记录的路径值,则更新该路径值。3. 迭代:重复步骤2,直到所有边都被松弛了|V|-1次,其中|V|是顶点的数量。4. 检测负权环:在第|V|次迭代中,如果还能更新某个顶点的最短路径值,则说明存在负权环。算法正确性证明:• 初始化:保证了所有顶点的最短路径值都是一个上界。• 松弛操作:确保了如果存在更短的路径,那么这个更短的路径会被找到并更新。• 迭代次数:由于每次迭代都可能更新最短路径值,最多需要|V|-1次迭代来确保所有可能的路径都被考虑过。• 检测负权环:如果在第|V|次迭代中还能更新某个顶点的最短路径值,这意味着存在一个环,使得通过这个环可以无限次地减少路径值,即存在负权环。Go 语言实现:package mainimport("fmt")const INF =int(1e9)// 表示无穷大func bellmanFord(graph [][]int, src int, V int)[]int{ dist :=make([]int, V)for i :=range dist { dist[i]= INF} dist[src]=0for i :=0; i < V-1; i++{for u :=0; u <len(graph); u++{for v, w :=range graph[u]{if dist[u]!= INF && dist[u]+w < dist[v]{ dist[v]= dist[u]+ w}}}}// 检测负权环for u :=0; u <len(graph); u++{for v, w :=range graph[u]{if dist[u]!= INF && dist[u]+w < dist[v]{ fmt.Println("Graph contains a negative weight cycle")returnnil}}}return dist}func main(){// 图的邻接矩阵表示,graph[i][j] 表示从 i 到 j 的边的权重,如果没有直接连接则为0// 如果存在负权环,这个例子中应该包含负值 graph :=[][]int{{0,5,0,0},{0,0,-2,0},{0,0,0,3},{0,0,0,0},} V :=4// 顶点数量 src :=0// 源点 dist := bellmanFord(graph, src, V)if dist !=nil{ fmt.Println("Shortest distances from the source vertex:", dist)}}这段代码实现了贝尔曼-福特算法,并在检测到负权环时打印出相应的信息。如果需要找出负权环的具体结点,可以进一步修改算法来记录路径,然后在检测到负权环时回溯这些路径。
混元:要解决这个问题,我们可以使用Bellman-Ford算法的一个变种。Bellman-Ford算法原本用于计算从单一源点到所有其他顶点的最短路径,即使图中存在负权重边。当图中存在负权重环路时,Bellman-Ford算法可以检测到这一点。我们可以对这个算法进行修改,以便不仅检测负权重环路,还列出环路上的所有顶点。
以下是Go语言实现的算法步骤:
1. 初始化距离数组dist,将起始顶点的距离设为0,其他顶点的距离设为无穷大。2. 对所有边进行|V|-1次松弛操作,其中|V|是顶点的数量。每次松弛操作都会尝试更新通过每条边到达的顶点的最短距离。3. 在完成|V|-1次松弛操作后,再进行一次额外的松弛操作。如果这次操作还能更新距离,说明图中存在负权重环路。4. 为了找到负权重环路上的顶点,我们需要反向追踪更新后的距离。从检测到负权重环路的顶点开始,沿着更新了距离的边反向追踪,直到回到起点,这样就找到了一个负权重环路。5. 重复步骤4,直到所有负权重环路都被找到。下面是Go语言的实现代码:
package mainimport("fmt""math")typeEdgestruct{from, to int weight float64}func findNegativeCycle(graph [][]Edge)[][]int{ n :=len(graph) dist :=make([]float64, n) prev :=make([]int, n)for i :=range dist { dist[i]= math.Inf(1) prev[i]=-1} dist[0]=0// 假设从顶点0开始// 进行|V|-1次松弛操作for i :=0; i < n-1; i++{for u :=0; u < n; u++{for _, e :=range graph[u]{if dist[u]+e.weight < dist[e.to]{ dist[e.to]= dist[u]+ e.weight prev[e.to]= u}}}}// 检测负权重环路并记录路径var cycles [][]intfor u :=0; u < n; u++{for _, e :=range graph[u]{if dist[u]+e.weight < dist[e.to]{// 找到一个负权重环路 cycle :=[]int{}for v := e.to; v != u; v = prev[v]{ cycle =append(cycle, v)} cycle =append(cycle, u) cycles =append(cycles, cycle)}}}return cycles}func main(){ graph :=[][]Edge{{{0,1,-1},{0,2,4}},{{1,2,3},{1,3,2},{1,4,2}},{},{{3,1,1},{3,2,5}},{{4,3,-3}},} cycles := findNegativeCycle(graph)for _, cycle :=range cycles { fmt.Println(cycle)}}这段代码首先定义了一个Edge结构体来表示图中的边,然后实现了findNegativeCycle函数来找到所有负权重环路并返回它们的顶点列表。最后,main函数提供了一个示例图,并调用findNegativeCycle函数来打印出所有的负权重环路。
算法的正确性基于Bellman-Ford算法的原理,该算法能够处理负权重边并在存在负权重环路时检测到它。通过反向追踪更新后的距离,我们可以找到构成负权重环路的顶点。