李后强  中国系统科学研究会副理事长、成都市社会科学界联合会主席、二级教授、电子科技大学博士生导师

李贤彬  四川省社会科学院副教授、博士

（李后强参加学术研讨会）

前言

一般讲，“复杂学”就是研究复杂性或者非线性系统的科学。复杂学深刻揭示，世界本来很简单，是人把世界搞复杂了，关键是人心复杂。从组成来看，物质世界基本单元是光子（表现是量子）。有了光子就有了世界。从运行机制看，元素之间协同耦合，各种层次的无限重复循环如自组织（SOC）、分形（fractal）等等，就可以产生复杂性。可以肯定，世界的成分简单，机制简单，规则简单。复杂性是由多成分、多循环、多耦合造成的，这是认识复杂性系统的重要原则。世界各种运动都满足“最小作用量原理”，必须简单！“最小作用量原理”，即能量与时间的积分等于零δS=∫Ldt=0，耗能最小、用时最少、行走最短，与拉格朗日函数L（L=T-V，动能减去势能）有关。丹麦学者帕。巴克撰写的《大自然如何运作——关于自组织临界性的科学》（北京大学出版社，2024年），基本观点是，大自然按照“黄金分割率”生长和运行的（比如斐波拉契数列Fibonacci sequence），大多数情况是“分形”（fractal）结构，值得一读，读后会让你变得更聪明，减少许多烦恼。

（一）从物质结构看复杂性中的简单性

我们看看太阳光、基本粒子和电子相互作用，以及费米子和玻色子，就明白了复杂性中的简单性。

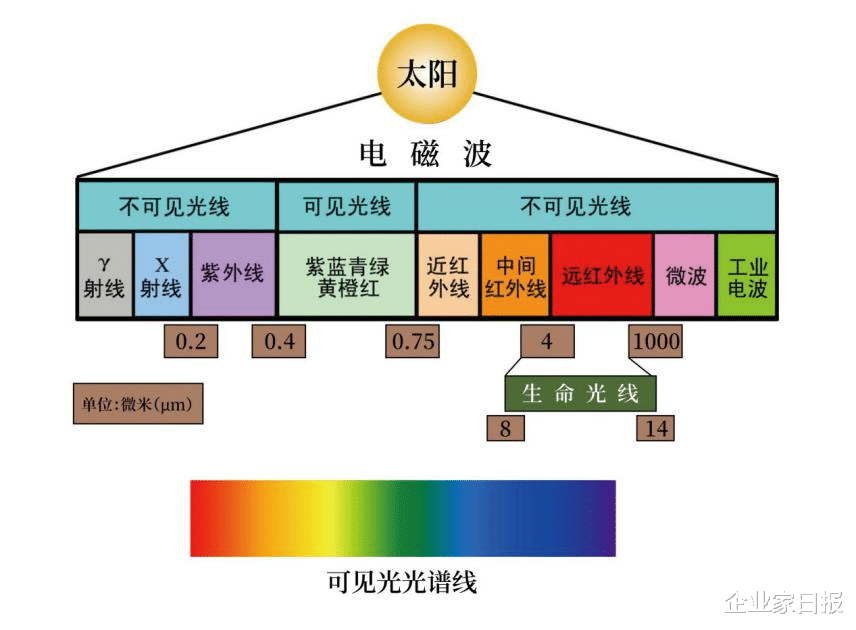
（李后强韩毅绘制）

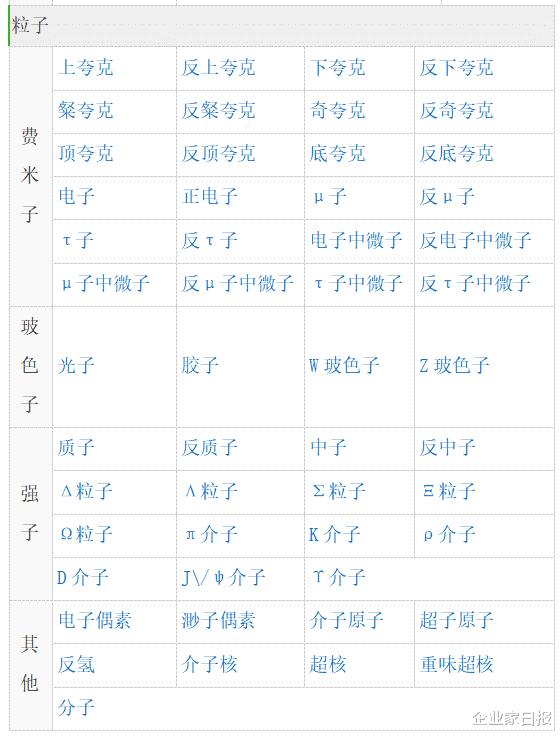
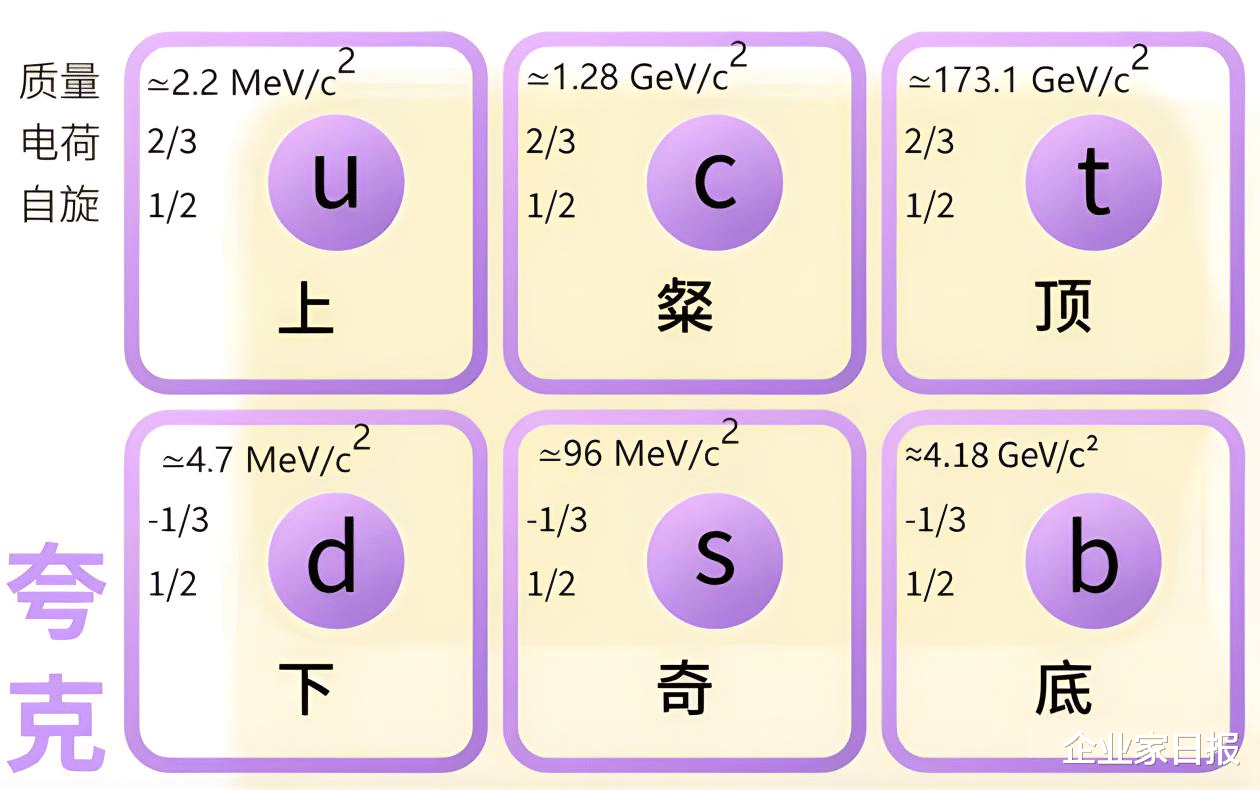
（夸克与胶子及其特征数据，李后强韩毅绘制）

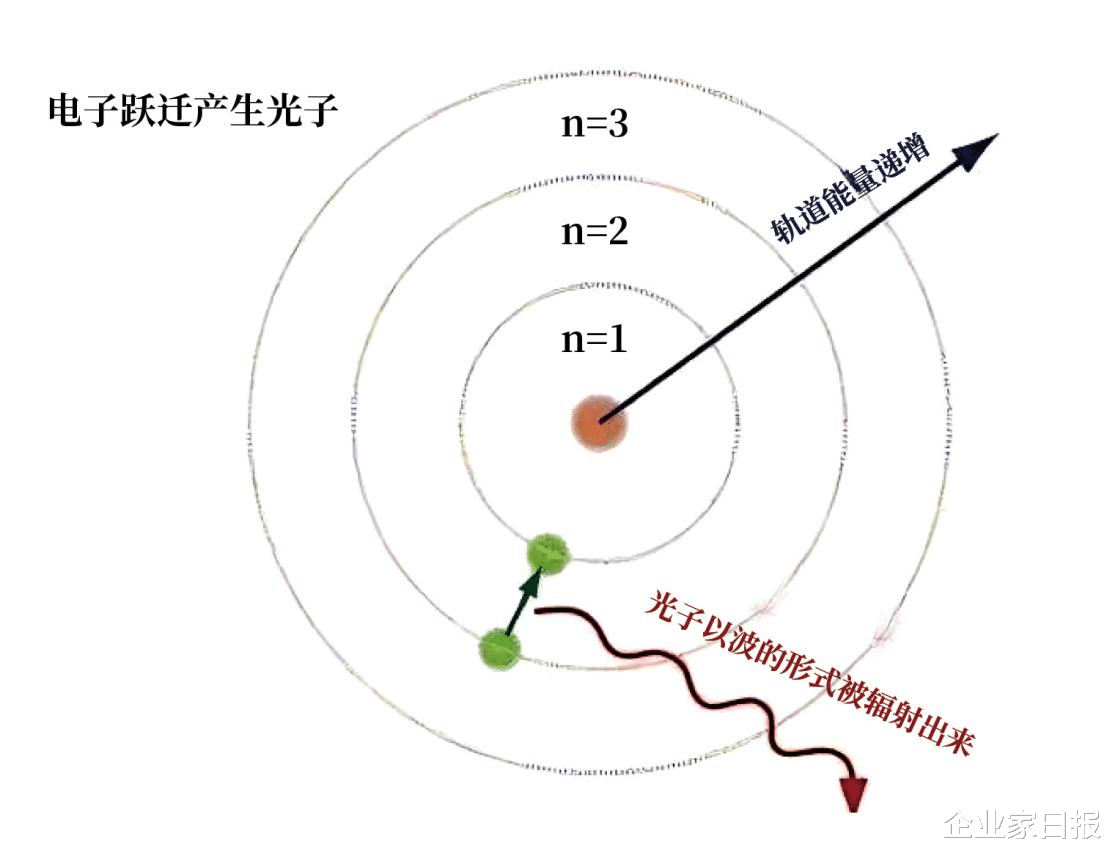
（原子激发态示意图李后强韩毅绘制）

（正负电子相遇湮灭，李后强韩毅绘制）

（玻色子与费米子差异，李后强绘制）

（李后强在圆桌会议上发言）

尽管科学家们发现了大量微观粒子，但从性质来看最基本的是两种即“费米子”和“玻色子”。‌费米子和玻色子的主要区别在于它们的统计性质、‌自旋量子数以及它们在物质中的作用不同。‌‌费米子‌：遵循‌费米-狄拉克统计；自旋量子数为半整数（如电子的自旋为1/2）；不遵守‌泡利不相容原理，即两个费米子不能处于完全相同的状态。‌玻色子‌：遵循‌玻色-爱因斯坦统计；自旋量子数为整数（如‌光子的自旋为1）；遵守泡利不相容原理，多个全同玻色子可以同时处于同一个量子态；在低温时可以发生玻色-爱因斯坦凝聚。‌费米子‌是构成物质的基本粒子，如电子、质子、中子等，它们是物质的基本结构单元。‌玻色子‌是传递基本相互作用的中介、桥梁、纽带，如电磁相互作用（光子）、弱相互作用（W和Z玻色子）、强相互作用（胶子），它们是物质之间相互作用的媒介。

科学家能够把两个费米子结合在一起成为具有玻色子性质的“费米子库柏对”（类玻色子），这样使费米子对冷凝，成为费米凝聚。“玻色一爱因斯坦凝聚态”物质由玻色子构成，其行为像一个大的超级原子。而“费米子凝聚态”物质采用的是费米子，当物质冷却时，费米子逐渐占据最低能态，但它们处在不同的能态上，更像爬楼梯一样由低到高占据所有可能的能级。

（二）由“复”与“杂”构成复杂

研究复杂学，首先要明白什么是“复”和“杂”。“复”表示重复、复合，多次做某事或多次出现，或者由两个或多个部分组成。“杂”表示混合、多样、不纯，强调多种不同的东西混在一起，表示种类多、不单一、不纯洁，含有杂质或表示没有秩序或不规整。从主要区别看，杂：侧重于多样性、混合性和不整齐性；复：侧重于重复、恢复、复合。 杂：常用于描述混乱状态；复：常用于描述反复多次。在数学中，“复”通常指“复数”（Complex Number）。复数是一种扩展了实数系统的数，用于解决一些在实数范围内无法解决的问题。复数的定义为  z = a + bi ，其中： a 和 b是实数， i是虚数单位，满足 i2 = -1 。显然，数学的复数由虚与实组成，有共轭复数、模（绝对值）、辐角（幅角）等概念。复数主要用于解决信号（光子）传输问题，如电流、频谱、波函数和量子态等等，应用十分广泛。“复”与“杂”两个字（元素）本身就非常麻烦和棘手，二者协同耦合的非线性作用还能产生1+1>2效应，也许出现无限可能性，因此可以形成“复杂性”与“复杂学”。从研究的角度，可以分为“微观复杂学”（小于原子尺度）和“宏观复杂学”（大于原子尺度）。

（李后强与专家学者交流）

（三）复杂背后是简单

大道至简，道法自然。大自然本身很简单，“复”与“杂”是其外在表面特征，原始初态是单一纯洁的，底层逻辑和作用机制是清晰易见的。我们看到的往往是事物的表面现象，这些现象可能是复杂、混乱的。深入探究后，可能会发现这些复杂现象背后的本质是简单的，遵循一些基本的规律或原则。我们要尊重自然、敬畏自然、顺应自然，从大自然中去发现简单规则，这就是“道法自然”。

科学的一个重要目标就是从复杂的现象中提炼出简单的规律。例如，牛顿的三大运动定律简洁地解释了物体的运动规律。数学模型能够用简单的公式或方程来描述复杂的现象，如薛定谔方程描述了量子系统的演化。奥卡姆剃刀原则告诉我们，在解释现象时，应该选择最简单的解释。简单性通常意味着更高的可验证性和预测能力。最高的智慧和真理往往是简单的，“真佛才说家常话”，这就是“大道至简”。

在设计和工程领域，简洁的设计往往更可靠、更易于维护。例如，苹果公司的产品设计以其简洁著称。在管理和决策中，化繁为简可以帮助人们更清晰地看到问题的核心，从而做出更有效的决策。

人类的认知资源是有限的，过于复杂的信息会增加认知负荷，导致理解和处理困难。简化信息可以帮助人们更好地理解和应对复杂情况。尽管天气系统非常复杂，但气象学家通过简单的数学模型和物理定律，能够预测未来的天气变化。一个好的管理者会把复杂的问题分解成简单的任务，让团队成员更容易理解和执行。人生的道路可能充满曲折，但最终的目标往往是简单的——追求幸福和内心的平静。

（四）寻找简单的路径

“复杂的真相是简单”提醒我们在面对复杂问题时，不要被表面的复杂性所迷惑，而是要寻找其背后的简单规律和基本原则。通过这种方式，我们可以更好地理解和解决复杂的问题。从复杂中找到简单是一项挑战，但通过一些系统的方法和思维方式，可以有效地简化复杂的问题。

1.明确目标。 清晰地定义你要解决的问题或达到的目标。明确的目标可以帮助你集中精力，避免被无关的信息分散注意力。确定哪些方面是最重要的，哪些是可以暂时忽略的。

2. 分解问题。 将大问题拆解成更小、更易管理的部分。每个小问题都可以单独分析和解决。将复杂系统分成独立的模块，每个模块负责一个特定的功能。

3.识别关键因素。找出影响问题的关键因素。这些因素通常是问题的核心，解决了它们，整个问题就迎刃而解。分析各个因素之间的因果关系，找出哪些是根本原因，哪些是次要原因。

4.使用模型和框架。通过抽象化来简化问题。例如，用数学模型、流程图或概念图来表示复杂的关系。利用现有的理论、模型或框架来指导分析。例如，SWOT分析（优势、劣势、机会、威胁）可以帮助你全面地评估一个项目。

5.去除冗余。去除不必要的信息和步骤，只保留最关键的部分。优化流程，去除冗余环节，提高效率。

6.可视化。使用图表、流程图、思维导图等视觉工具来展示信息，可以帮助你更直观地理解复杂的关系和结构。通过故事板或场景描述来简化复杂的流程或概念。

7.寻求反馈。与他人讨论你的想法和解决方案，听取不同的意见和建议。外部视角有时能帮助你发现新的简化方法。如果可能的话，咨询相关领域的专家，他们可能有更深入的理解和经验。

8. 持续优化。简化是一个持续的过程，要不断迭代改进，不断调整和优化方法，使之更加高效和有效。定期反思和总结，看看哪些方法有效，哪些需要改进。

9. 培养直觉。通过大量的实践和经验积累，培养对复杂问题的直觉。直觉可以帮助你在短时间内抓住问题的本质。学会识别和应用常见的模式和规律，这些模式往往能简化复杂的问题。

10.保持开放心态。保持开放的心态，灵活应变，接受新的信息和观点。有时候，新的信息可能会改变你对问题的理解，从而找到更简单的解决方案。持续不断学习新的知识和技能，提升自己的分析和解决问题的能力。

可以应用大数据特别是人工智能（AI）分析涉及大量数据和变量的复杂体系（如2024年诺贝尔物理学奖、化学奖），从而快速识别关键趋势和模式，简化分析过程，提高解决问题的效率和质量。

（五）推进宏观复杂学研究

宏观复杂学（Complexity Science）是一门跨学科的研究领域，旨在研究和理解复杂系统的行为和特性，涉及多个学科包括物理学、生物学、计算机科学、经济学、社会学等。复杂系统是由大量相互作用的组件组成的系统，这些组件之间的交互会产生“涌现”行为，即整体表现出的特性不能简单地从单个组件的特性推导出来。复杂系统中的相互作用通常是非线性的，即输入和输出之间不成比例关系。即微小的变化可能导致巨大的后果。复杂系统有自适性，其中的组件能够适应环境变化，通过学习和进化来改进自身的功能。比如生态系统中的物种进化、经济市场中的企业竞争等。复杂系统有自组织特征，能够在没有外界干扰的情况下自发地形成有序结构，比如蜂巢的建设、细胞的分化等。特别是自组织临界性（SOC）值得高度重视，研究系统如何自发地达到一种临界状态，在这种状态下，小的扰动可以引发大的变化。

宏观复杂学通常采用的方法——

1.计算机模拟：通过计算机模拟来研究复杂系统的行为，特别是那些难以通过实验直接观察的系统。比如多主体建模（Agent-Based Modeling, ABM）、元胞自动机（Cellular Automata）等。

2. 网络分析：研究系统中组件之间的连接和相互作用，揭示网络结构对系统行为的影响。比如图论、社会网络分析等。

3. 动力系统理论：研究系统随时间演变的规律，特别是非线性动力系统的稳定性、分岔和混沌行为。比如微分方程、相空间分析等。

4. 信息理论：研究系统中信息的传递和处理，特别是在不确定性和随机性较高的情况下。比如熵、互信息等。

宏观复杂学的应用领域，主要是生物学和生态学，比如基因调控网络，研究基因之间的相互作用及其对细胞功能的影响，研究物种间的相互作用和生态平衡的维持。研究非线性动力系统的不可预测性和敏感依赖性，确定性系统内部存在的随机性，湍流和物质在宏观尺度上的集体行为。研究智能系统的学习和适应能力，研究大规模分布式系统的协调和优化。研究市场价格的波动和投资者行为。研究社会关系网的结构和动态变化。研究交通流量的管理和优化。研究城市发展的动态过程和可持续性。

宏观复杂学可以通过多种方法和技术，揭示复杂系统中的涌现行为、非线性、适应性和自组织等特性。宏观复杂学的应用范围广泛，涵盖了自然科学、社会科学和工程技术等多个领域。通过宏观复杂学的研究，我们可以更好地理解和应对复杂世界中的各种挑战，发现大自然的真相其实很简单。

（李后强、李贤彬2024年11月23日-24日在第十三届全国复杂性与系统科学哲学学术研讨会上的报告）