这的确是一个让人不免思考的问题。狭义相对论已经为我们提供了明确的解答:无论怎样,你观测到的我的速度都是光速不变。

为了深入理解这一答案,让我们首先探讨为何这个问题会引发思考。你的直觉可能会告诉你:“按照地面参考系来看,你的速度肯定是飞船速度与你相对于飞船的速度之和。”对吧?
但在相对论的世界里,这种直觉是错误的。
让我们用数学来简洁地表达这一问题。有两个做匀速直线运动的相对参照系,我们称之为1号和2号。从1号参照系来看,2号的速度是u,而一个物体在2号参照系中的速度是v,并且这两个速度是同向的。我们把这个物体在1号参照系中的速度记作v'。于是,你的直觉公式就是:
v' = v + u。
这个公式名为“伽利略变换”,由意大利科学家伽利略所揭示。
在大多数日常生活中,伽利略变换确实准确无误。举个例子,你在行驶的汽车上奔跑,你相对于汽车的速度是5米每秒,而汽车相对于地面的速度为15米每秒,那么你相对于地面的速度确实是两者之和,即20米每秒。
然而,相对论却告诉我们,伽利略变换仅是一个近似值,真正的公式其实是这样的:
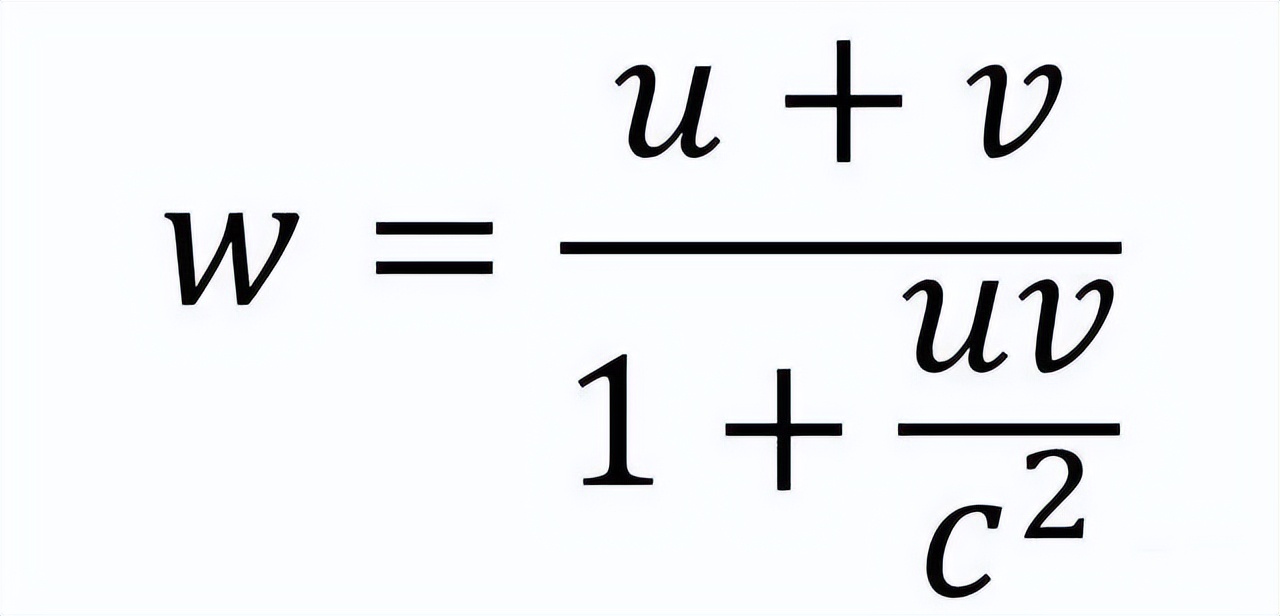
换言之:v' = (v + u) / (1 + uv/c平方)。
公式中的c代表光速,大约为30万公里每秒,c为光速。这个公式名为“洛伦兹变换”,是由荷兰科学家洛伦兹所发现的(请注意,不是爱因斯坦,虽然爱因斯坦建立了狭义相对论体系,但洛伦兹变换在其之前已被提出)。它实际上是在伽利略变换的基础上,加入了一个修正因子1 + uv/c平方。
洛伦兹变换向我们揭示了什么?
若u和v与光速相比微不足道,那么uv/c平方趋近于0,分母1 + uv/c平方接近1,于是v'基本上等于v + u,我们又回到了伽利略变换的世界。

在上述例子中,u = 15米每秒,v = 5米每秒,情况正是如此。如果你将精确的公式代入计算,你会发现修正结果小到了10的负16次方,这意味着你需要到小数点后第16位才能看出差异,这种微小的效应甚至超出了现代仪器的探测极限。
但当u或v达到光速的量级时,情况就大不相同了。这时,你必须认真对待1 + uv/c平方这个修正因子。
例如,假设u = v = c/2,即你和汽车都以光速的一半相对地面运动,结果会是怎样?你的直觉可能会是v' = c,即你相对地面的速度为光速。但实际上,应用洛伦兹变换,我们会得到v' = (1/2 + 1/2) / (1 + 1/4) c = 1 / (5/4) c = (4/5) c。这意味着在地面上看来,你的速度仅为光速的80%,并未达到光速。
再比如,若u = v = (3/4) c呢?你的直觉可能会告诉你v' = (3/2) c,这似乎意味着你超越了光速(这曾是许多人设想的超光速方法)。但实际上,使用洛伦兹变换,我们得到的结果是v' = (3/4 + 3/4) / (1 + 9/16) c = (3/2) / (25/16) c = (24/25) c。这表明你的速度实际上更接近光速,达到了96%,但仍未超过光速。
实际上,通过简单的数学证明可以得知,只要u和v都不超过光速,那么通过洛伦兹变换得到的v'也必然不会超过光速。也就是说,试图通过运动叠加的方式达到光速是不可能的。
回到题目中的情况,假设u = c,你的直觉可能会是v' = v + c。但使用洛伦兹变换,我们得到:
v' = (v + c) / (1 + v/c),简化后就是光速c。
这意味着,在地面上看来,你的速度仍旧是光速。
你可能以为结果会是光速加上v,但实际上,由于洛伦兹变换的修正,v所带来的那部分速度刚好被抵消了,最终得到的仍是光速。
通过观察,你会发现,只要u和v中有一个等于光速c,那么v'就等于光速。即使两者都等于光速,v'还是光速。

经常会有人问:“如果两束光相对而行,那么其中一束光相对于另一束的速度是不是2倍光速?”现在你应该知道答案了,依然是光速。
总结来说,光速具有一种独特的性质,那就是它能抵抗一切试图通过变换参照系来增加其速度的尝试。无论你怎样改变参照系,光速始终如一,既不会增加,也不会减少。这正是相对论的基本原理之一,叫做“光速不变原理”。
最后,有两点需要特别提醒。
首先,这道题目本身有点问题,因为根据相对论,只有“静质量”为零的物体如光子才能以光速运动,像飞船这种“静质量”不为零的物体是无法达到光速的。因此,题目应该改为“在飞行的飞船上有一束光,在地面看来它比光速快吗?”尽管如此,本文的讨论并没有因此改变,因为在洛伦兹变换中,u和v的地位是对称的,互换两者得到的公式是相同的。

其次,洛伦兹变换似乎违反了我们的日常直觉,但科学界已经普遍接受了它是正确的。这并非因为科学家喜欢挑战传统,而是因为它与实验数据吻合无误。如果你坚持使用伽利略变换,可能会预测出一些错误的实验结果。例如,有人曾通过测量在地球运动不同方向上的光速差异,试图确定地球在宇宙中的绝对速度,这一实验被称作“迈克尔孙-莫雷实验”。但实验结果却是,在不同方向上光速没有可测量的差异!现在你应该能够体会到洛伦兹变换的强大之处了吧?