在之前各省花式命题的时候，数列一直是压轴风范，但自从进入全国卷后，数列直接从压轴题最后一题变成送分题第一题，虽然是沦为解答送分题，但有数列有一类问题，依旧有一定难度：数列的奇、偶项问题。

数列中的奇、偶项问题通常指的是在数列中，奇数项和偶数项分别遵循不同的规律或公式。解决这类问题时，需要分别考虑奇数项和偶数项的规律，然后综合起来解决问题。

老唐数学针对这类题型了一个总结，帮助同学突破这一类难题！

数列的奇偶项常见题型

①含有an+an+1=f(n)或an·an+1=f(n)；

②含有(-1)^(n)的类型；

③含有{a2n}，{a2n-1}的类型；

④已知条件明确的奇偶项问题．对于通项公式分奇、偶不同的数列{an}求Sn时，我们可以分别求出奇数项的和与偶数项的和，也可以把a2k-1+a2k看作一项，求出S2k，再求S2k-1=S2k-a2k.

例题

解析：

首先，我们注意到这是一个递推数列问题，并且递推关系涉及到前两项。由于递推关系中没有区分奇数项和偶数项，我们可以先尝试找出数列的通项公式，然后再求第10项。

写出递推公式的前几项

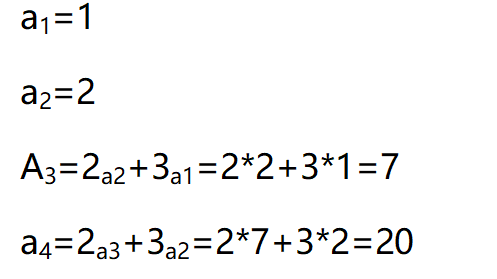
以此类推，我们可以计算出更多的项。

2.尝试找出通项公式

这是一个二阶线性递推关系，我们可以通过解特征方程来找到通项公式。特征方程为

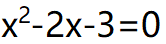
解得x=3或x=-1，因此通项公式可以表示为

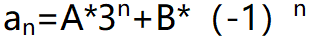
3.利用初始条件求解常数A和B的值。

将a₁=1和a₂=2带入通项公式，得到两个方程：

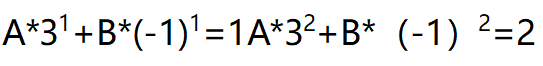
解这个方程组，我们可以得到A和B的值。

4.计算第10项

将n=10代入通项公式，计算a₁₀。

通过上述步骤，我们可以计算出A和B的值，然后代入n=10 来求得a₁₀。

如下：

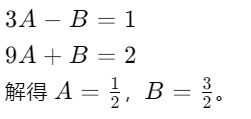
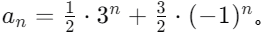
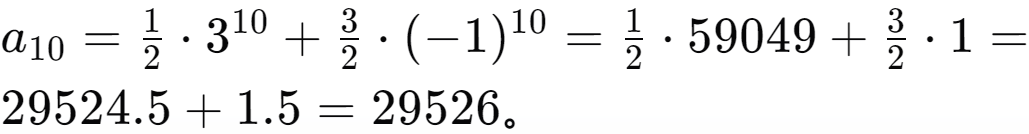
因此，数列的第10项a₁₀=29526

这个例题展示了如何通过递推关系和特征方程来求解数列的通项公式，并利用通项公式来计算特定项的值。